Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Треугольники"
Содержание
- 1. Презентация по теме "Треугольники"
- 2. О, сколько нам открытий чудныхГотовит просвещенья дух.И опыт – сын ошибок трудных,И гений – парадоксов друг. А.С.Пушкин
- 3. Сегодня на уроке надо: быть внимательным и
- 4. Соотнесите высказывание с его названиемТреугольник называется равнобедренным,
- 5. Заполни пропускиСумма углов треугольника равна ____ .Два
- 6. Найдите ошибки в текстеНекий ученик написал сочинение
- 7. Найди лишнее слово : сторона, вершина, диаметр,
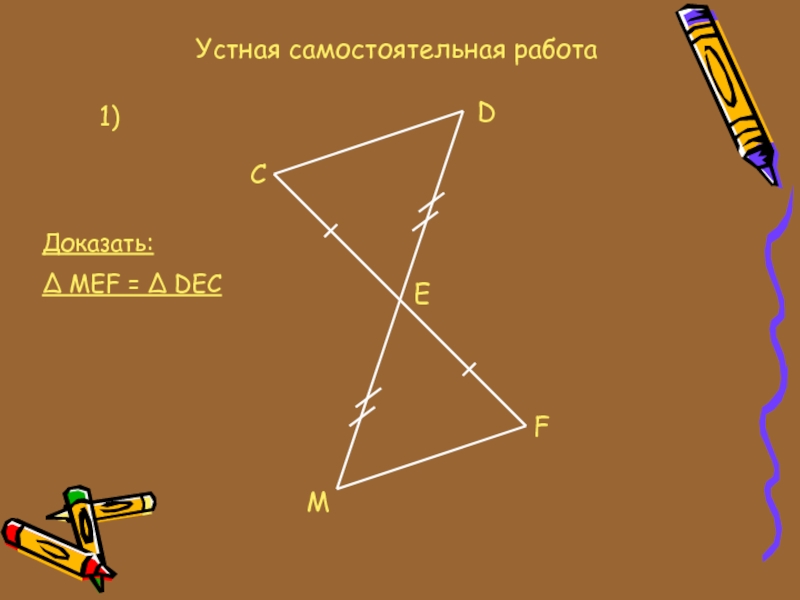
- 8. Устная самостоятельная работа1)CDEFMДоказать:∆ MEF = ∆ DEC
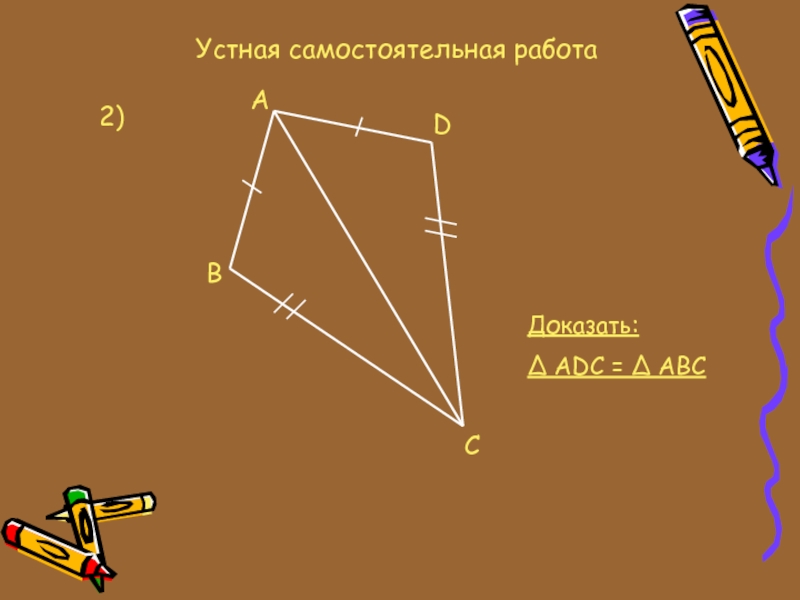
- 9. Устная самостоятельная работа2)CDABДоказать:∆ ADC = ∆ ABC
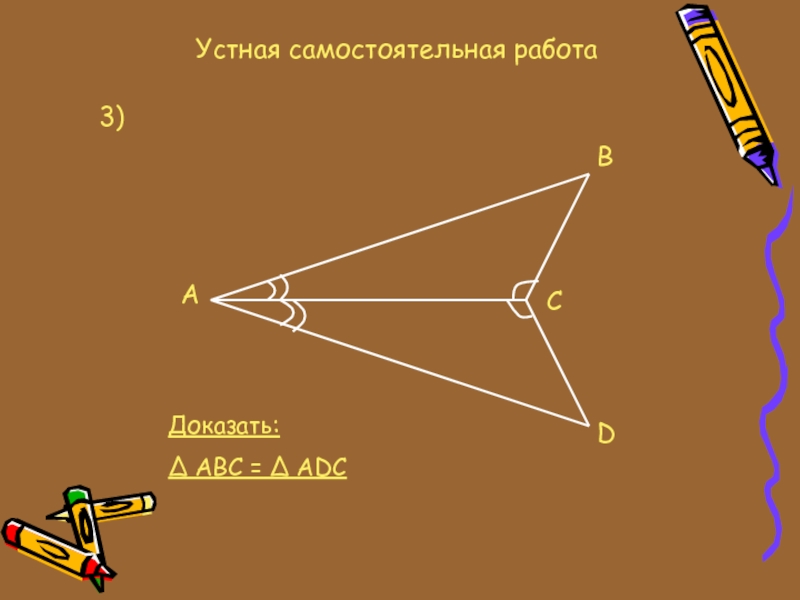
- 10. Устная самостоятельная работа3)ABCDДоказать:∆ ABC = ∆ ADC
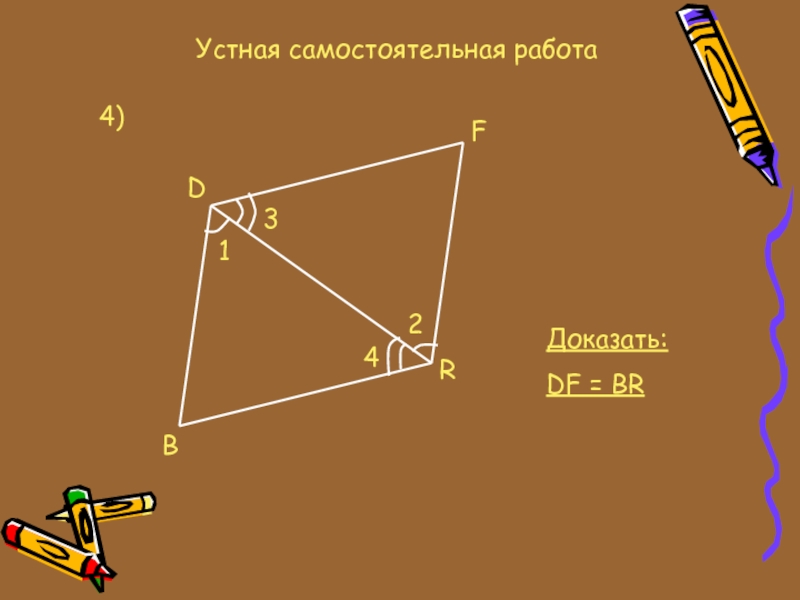
- 11. Устная самостоятельная работа4)DFRB3124Доказать:DF = BR
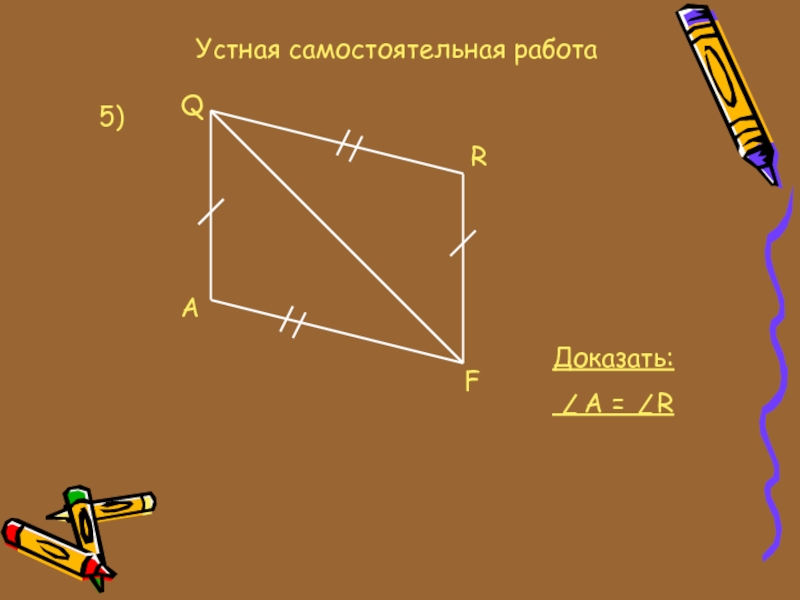
- 12. Устная самостоятельная работа5)QAFRДоказать: А = R
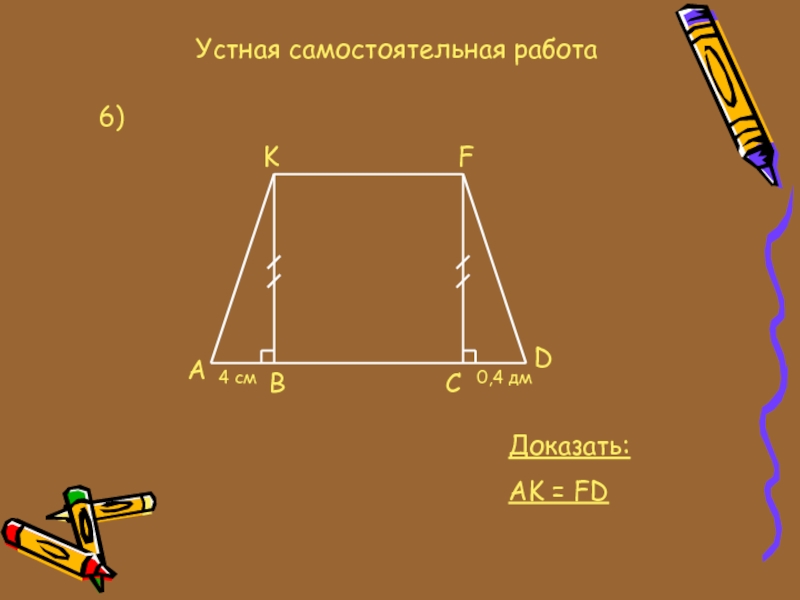
- 13. Устная самостоятельная работа6)AKFDCB4 см0,4 дмДоказать:AK = FD
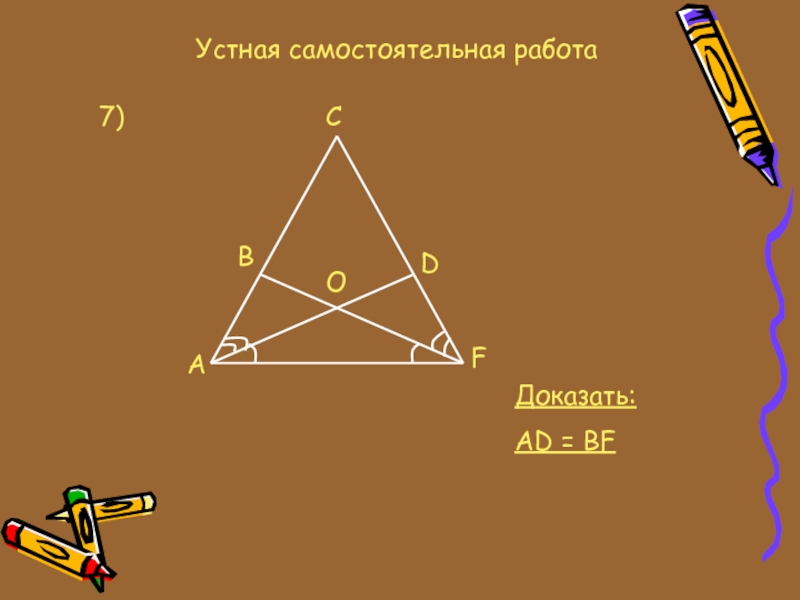
- 14. Устная самостоятельная работа7)ABCDFOДоказать:AD = BF
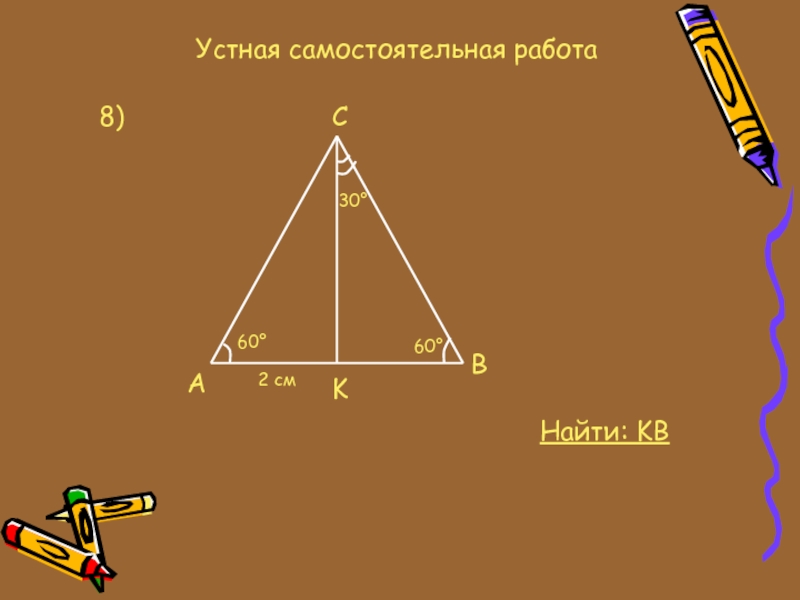
- 15. Устная самостоятельная работа8)ACBK60°60°30°2 смНайти: KB
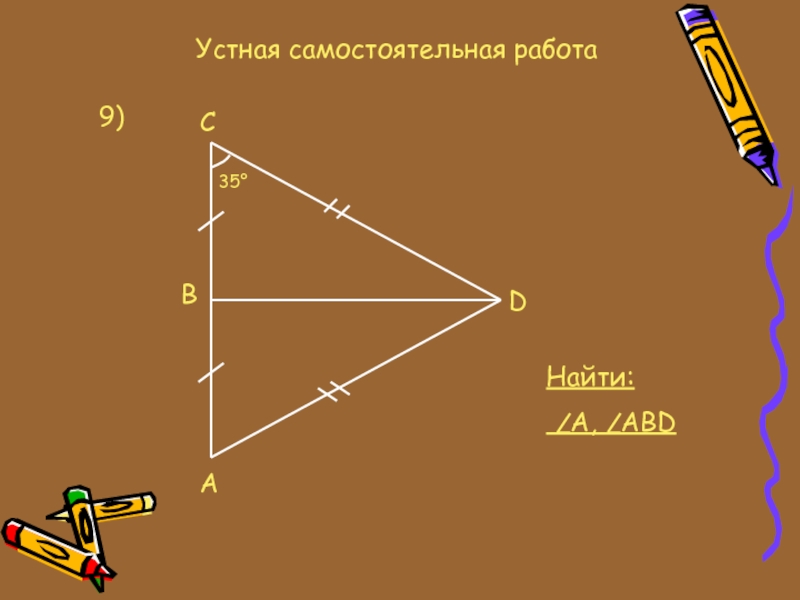
- 16. Устная самостоятельная работа9)CBAD35°Найти: A, ABD
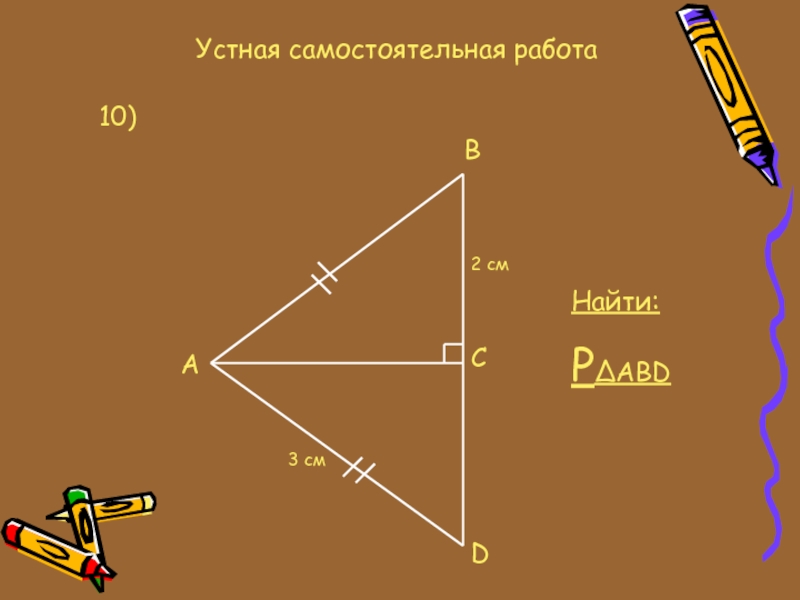
- 17. Устная самостоятельная работа10)ABCD2 см3 смНайти:P∆ABD
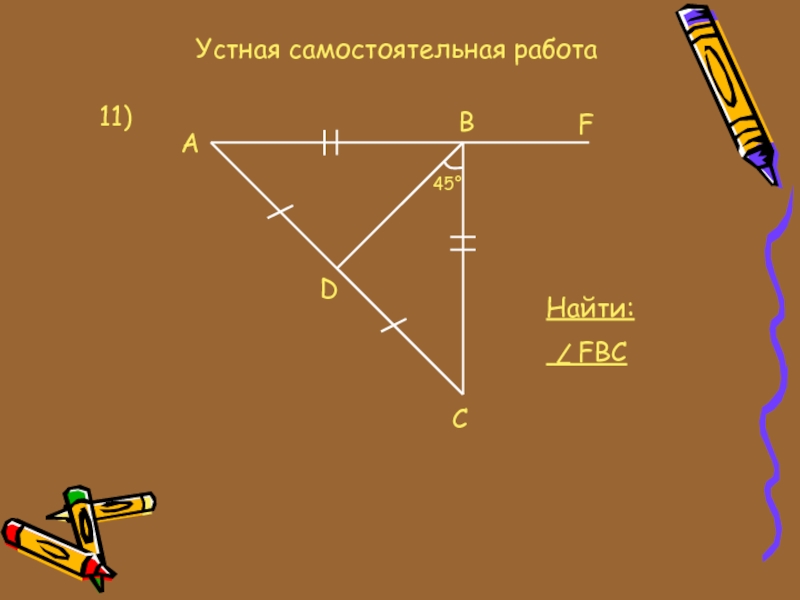
- 18. Устная самостоятельная работа11)ADCBF45°Найти: FBC
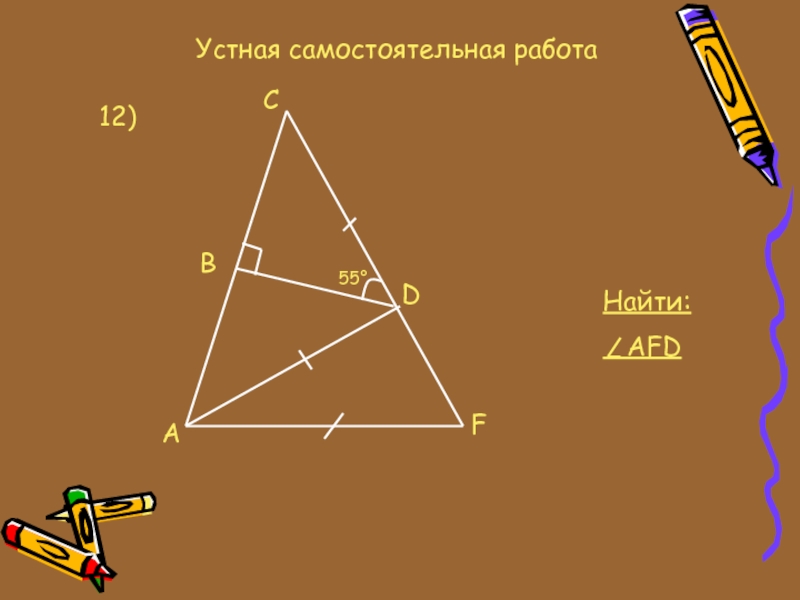
- 19. Устная самостоятельная работа12)ACBDF55°Найти: AFD
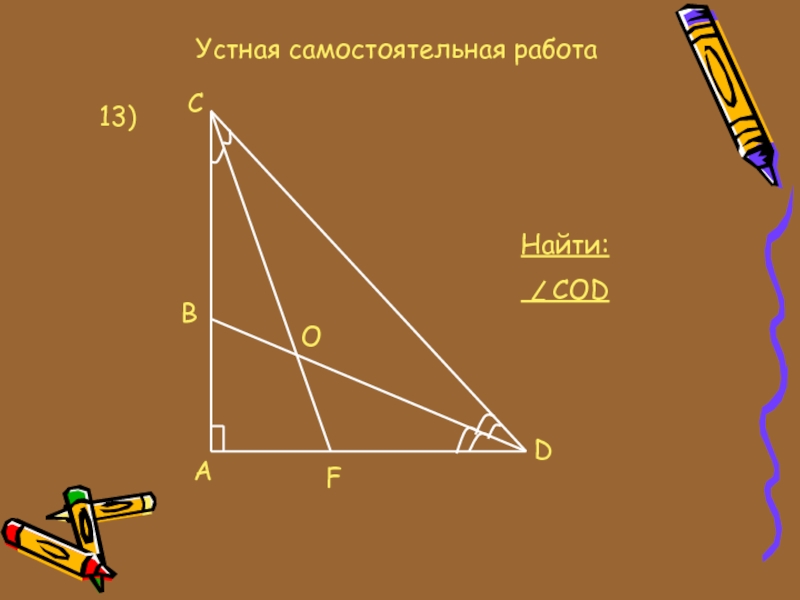
- 20. Устная самостоятельная работа13)ABCOFDНайти: COD
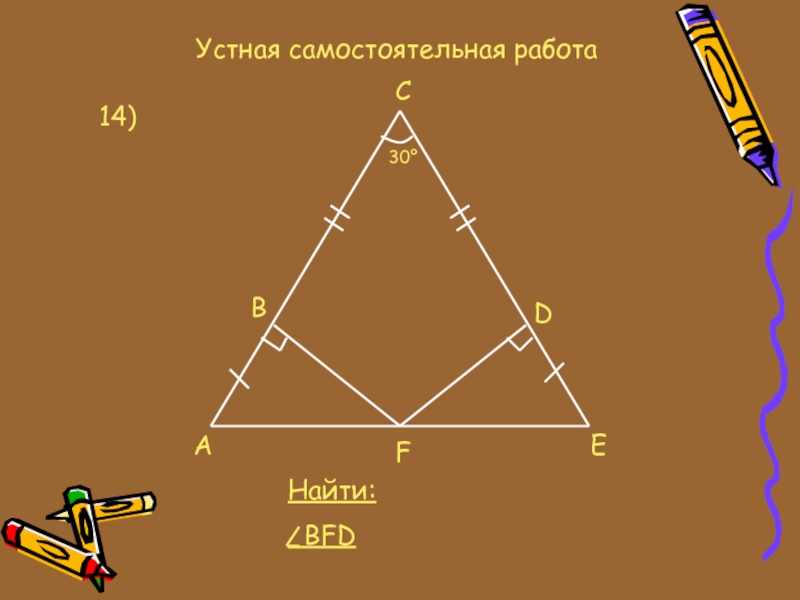
- 21. 14)Устная самостоятельная работаAFEBDC30°Найти: BFD
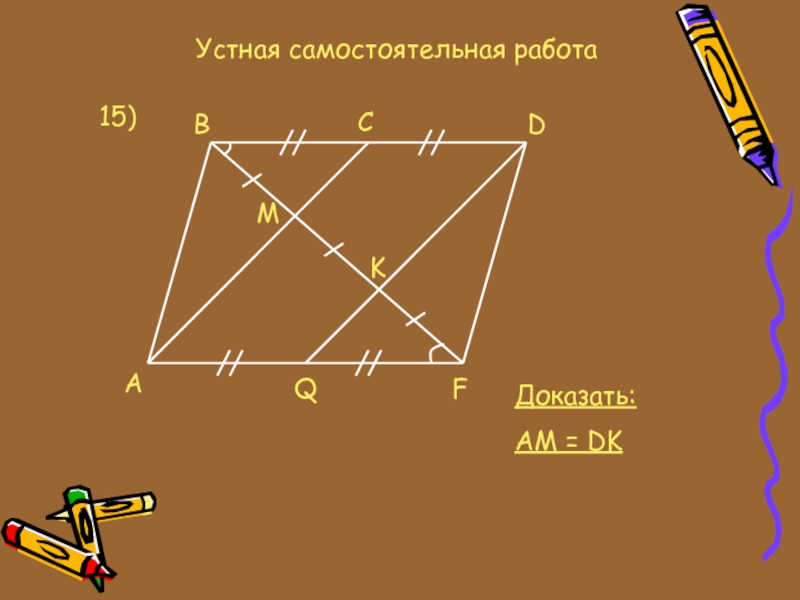
- 22. Устная самостоятельная работа15)AQFBCDMKДоказать:AM = DK
- 23. СинквейнКороткое литературное произведение, характеризующее предмет (тему), состоящее
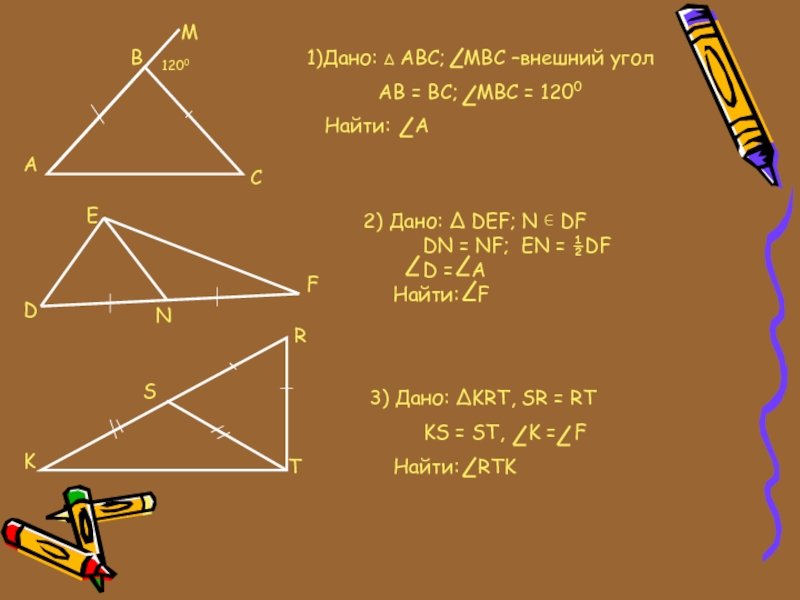
- 24. ВМAСDЕFNKSRT12001)Дано: ∆ АВС; МВС –внешний угол
- 25. Геометрия является самым могущественным средством для изощрения
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Сегодня на уроке надо:
быть внимательным и сообразительным;
не оставлять
ни одного вопроса без ответа;
на каждое задание затрачивать минимум
времени, но максимум усердия;не подглядывать, не подслушивать, не «проникать» в мысли соседа
Слайд 4Соотнесите высказывание с его названием
Треугольник называется равнобедренным, если две его
стороны равны
Если две стороны и угол между ними равны соответственно
двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
В равнобедренном треугольнике углы при основании равны.
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Сумма углов треугольника равна 180°.
Внешний угол треугольника Равен сумме двух внутренних углов, не смежных с ним.
Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
а) Определение треугольника;
б) Определение равнобедренного треугольника;
в) Свойство углов равнобедренного треугольника;
г) Аксиома существования треугольника равного данному;
д) Первый признак равенства треугольников;
е) Свойство углов треугольника;
ж) Свойство медианы равнобедренного треугольника;
з) Третий признак равенства треугольников;
и) Определение биссектрисы треугольника;
к) Свойство внешнего угла треугольника.
Слайд 5Заполни пропуски
Сумма углов треугольника равна ____ .
Два треугольника называются равными,
если ____ .
Треугольник ABC – равнобедренный, AB и BC –
боковые стороны. У него равны углы ____ .Треугольник называется равнобедренным, если ____ .
Если в треугольнике два угла равны, то он ____.
Внешним углом треугольника называется ____ .
В равнобедренном треугольнике медиана, проведенная к основанию, является ____ .
Если в треугольнике три угла равны, то он ____ .
Если две стороны и ____ одного треугольника равны соответственно двум сторонам и ____ другого треугольника, то _____ .
Треугольник называется прямоугольным, если _____ .
Слайд 6Найдите ошибки в тексте
Некий ученик написал сочинение по теме «Треугольники».
Вот некоторые фрагменты его сочинения:
Треугольник – это геометрическая фигура,
состоящая из трех точек, соединенных попарно отрезками.Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, то она будет и медианой, и высотой.
Чтобы доказать равенство треугольников, надо знать признаки равенства треугольников. Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольники равны.
Если сторона и любые два угла одного треугольника равны соответственно стороне и любым двум угла другого треугольника, то такие треугольники равны.
Если две стороны и любой угол одного треугольника равны соответственно двум сторонам и любому углу другого треугольника, то такие треугольники равны.
Внешний угол треугольника больше внутреннего угла, смежного с ним.
Слайд 7Найди лишнее слово : сторона, вершина, диаметр, основание, угол
Найди неизвестное
число:
Охарактеризуйте треугольник ABC и найдите неизвестный угол?
отдохни!
C
A
?
B
M
K
Слайд 23Синквейн
Короткое литературное произведение, характеризующее предмет (тему), состоящее из пяти строк,
которое пишется по определенному плану.
Точка
Невесомая, неширокая
Лежит, находится, ограничивает
Еле заметна
для меняКрапинка.
отдохни!
Слайд 24
В
М
A
С
D
Е
F
N
K
S
R
T
1200
1)Дано: ∆ АВС; МВС –внешний угол
АВ = ВС; МВС = 1200
Найти: А2) Дано: ∆ DEF; N ∊ DF
DN = NF; EN = ½DF
D = A
Найти: F
3) Дано: ∆KRT, SR = RT
KS = ST, K = F
Найти: RTK