Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Магические и латинские квадраты
Содержание
- 1. Магические и латинские квадраты
- 2. Составление магических квадратов
- 3. Исторические значимые магические квадратыМагический квадрат – древнекитайского
- 4. Магическая константа Сумма чисел в каждой
- 5. 1105Первые значения магических констант приведены в следующей таблице
- 6. Квадраты Ло Шу Единственный нормальный
- 7. Квадрат, найденный в Кхаджурахо (Индия) Самый ранний
- 8. Квадрат Альбрехта Дюрера Магический квадрат
- 9. Квадраты Генри Э. Дьюдени и Аллана У.
- 10. Построение магических квадратов Метод
- 11. Метод террас
- 12. Латинские квадраты. У истоков теории латинских
- 13. Использование латинских квадратов для планирования экспериментов
- 14. Слайд 14
- 15. Скачать презентанцию
Составление магических квадратов
Слайды и текст этой презентации
Слайд 2 Составление магических квадратов
представляет собой превосходную развивающую способность понимать идеи размещения, сочетания, симметрии, классификации, обобщения и т.д.
А. Обри
Слайд 3Исторические значимые магические квадраты
Магический квадрат – древнекитайского происхождения. Согласно легенде,
во время правления императора Ю из вод Хуанхэ (Желтой реки)
всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифыСлайд 4Магическая константа
Сумма чисел в каждой строке, столбце и
на диагоналях называется магической константой, M. Магическая константа нормального волшебного
квадрата зависит только от n и определяется формулой
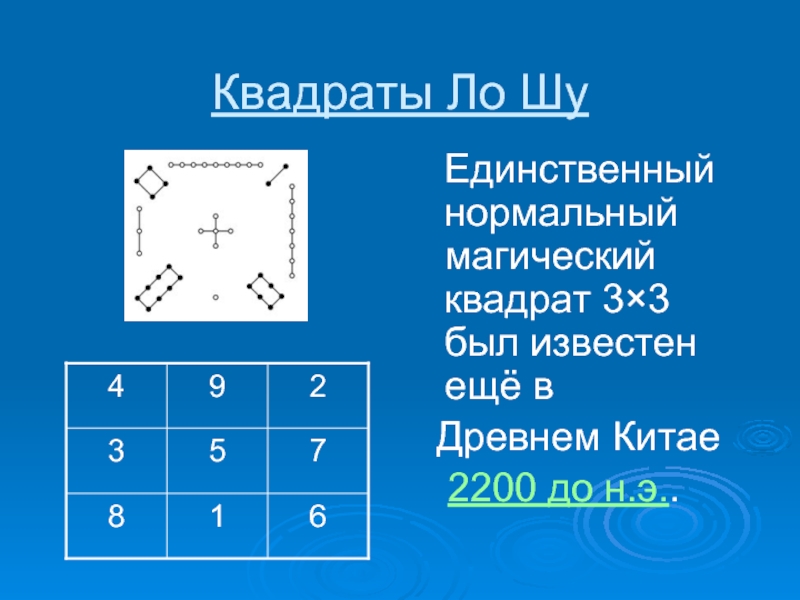
Слайд 6Квадраты Ло Шу
Единственный нормальный магический квадрат 3×3
был известен ещё в
Древнем Китае
2200
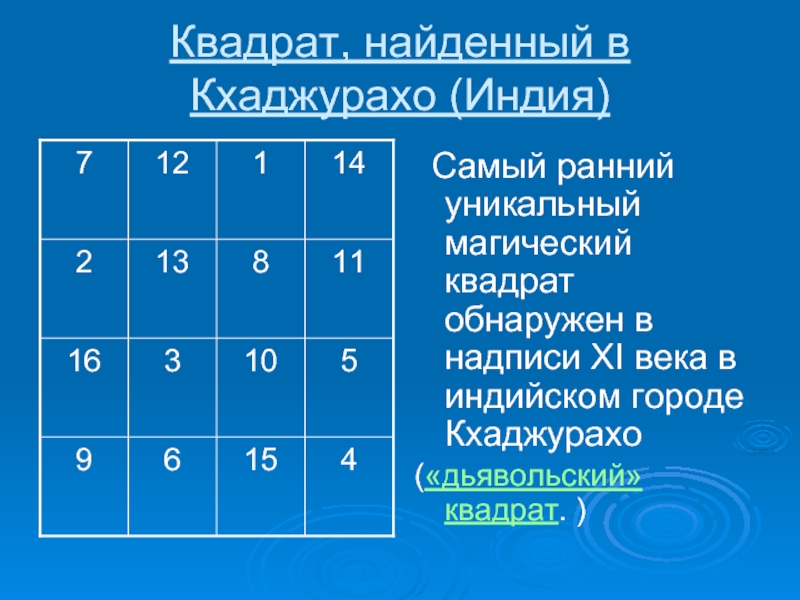
до н.э..Слайд 7Квадрат, найденный в Кхаджурахо (Индия)
Самый ранний уникальный магический квадрат
обнаружен в надписи XI века в индийском городе Кхаджурахо
(«дьявольский»
квадрат. )Слайд 8Квадрат Альбрехта Дюрера
Магический квадрат 4×4, изображённый на
гравюре Альбрехта Дюрера«Меланхолия», считается самым ранним в европейском искусстве. Два
средних числа в нижнем ряду указывают дату создания картины (1514).Слайд 9Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.
Представлены два
таких магических квадрата, заполненные в основном простыми числами.
Слайд 10Построение магических квадратов
Метод террас описан Ю.
В. Чебраковым в «Теории магических матриц». Я нашел и более
простой и доступный метод построения в книге «Волшебный мир логических квадратов» нашей землячки Макаровой М. В.Слайд 12Латинские квадраты.
У истоков теории латинских квадратов стоял Леонард
Эйлер (1707–1783). числа написаны в латинском квадрате так , что
встречаются в каждой строке и каждом столбце по одному разу :Слайд 13Использование латинских квадратов для планирования экспериментов
Латинские квадраты нашли
многочисленные применения как в математике, так и в ее приложениях
при постановке и обработке результатов экспериментов.
Теги