Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение приемов сгущения информации в процессе конструирования учебных материалов по математике
Содержание
- 1. Применение приемов сгущения информации в процессе конструирования учебных материалов по математике
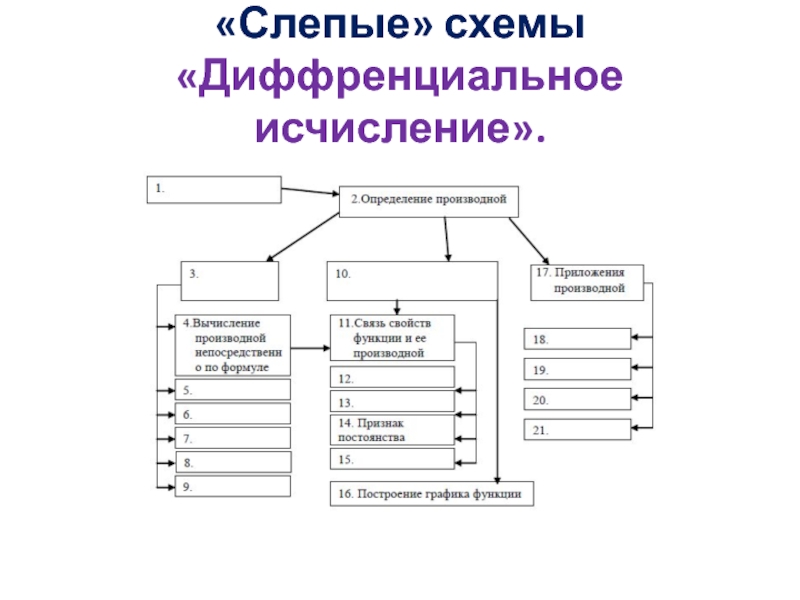
- 2. «Слепые» схемы «Диффренциальное исчисление».
- 3. Слайд 3
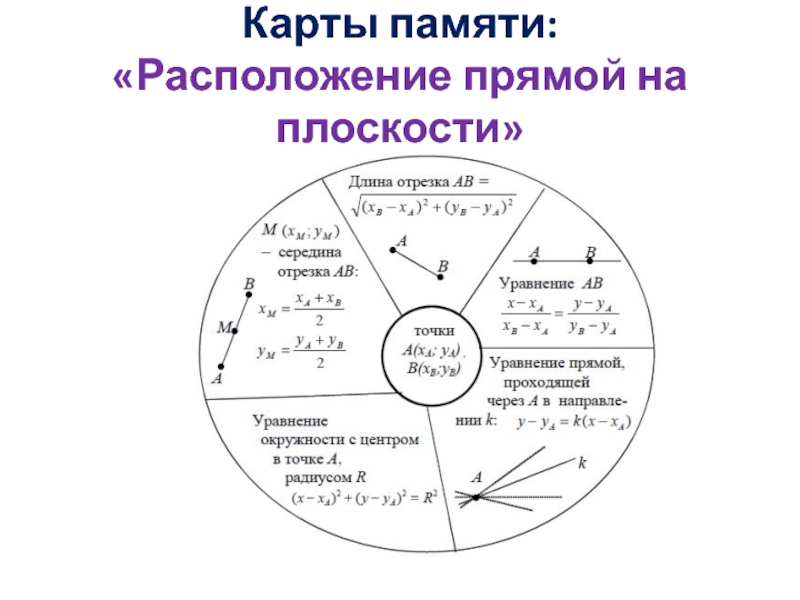
- 4. Карты памяти: «Расположение прямой на плоскости»
- 5. Логические средства укрупнения
- 6. Кратная запись. -заключается в сдваивании, страивании и т. д. записей.
- 7. «Матрёшка»- в одну запись можно свести две формулы
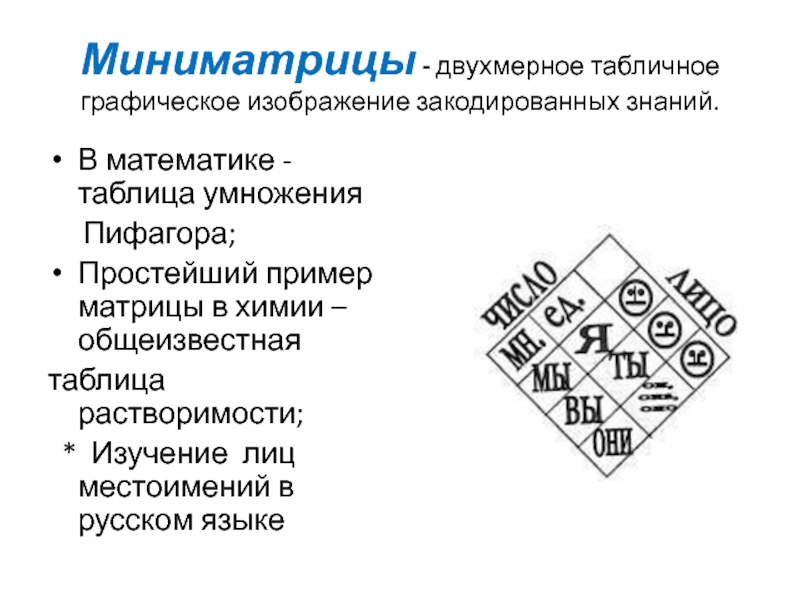
- 8. Миниматрицы - двухмерное табличное графическое изображение закодированных
- 9. Комбинированные элисторы (использованы разные виды кодирования (рисуночный,
- 10. Граф - схемы типа «Здание».
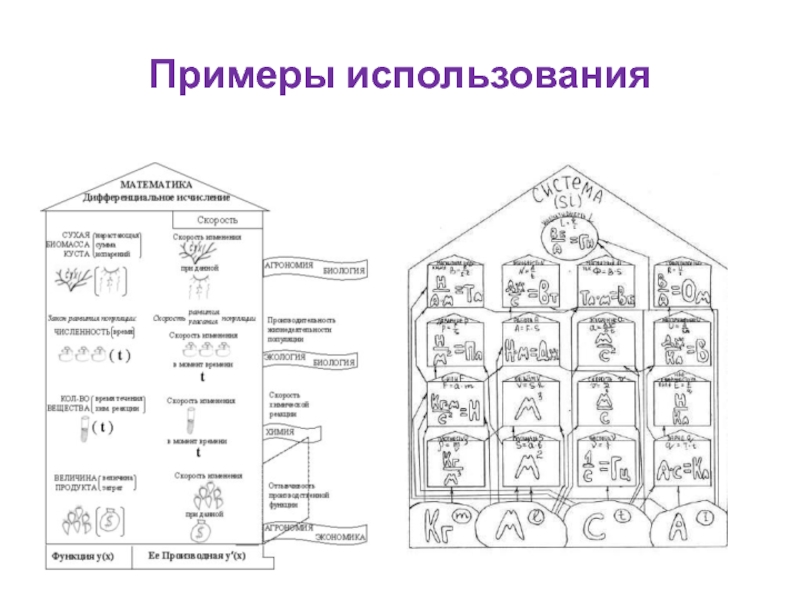
- 11. Примеры использования
- 12. Логико-смысловые модели
- 13. (ЛСМ) Предназначены для того, чтобы представлять и
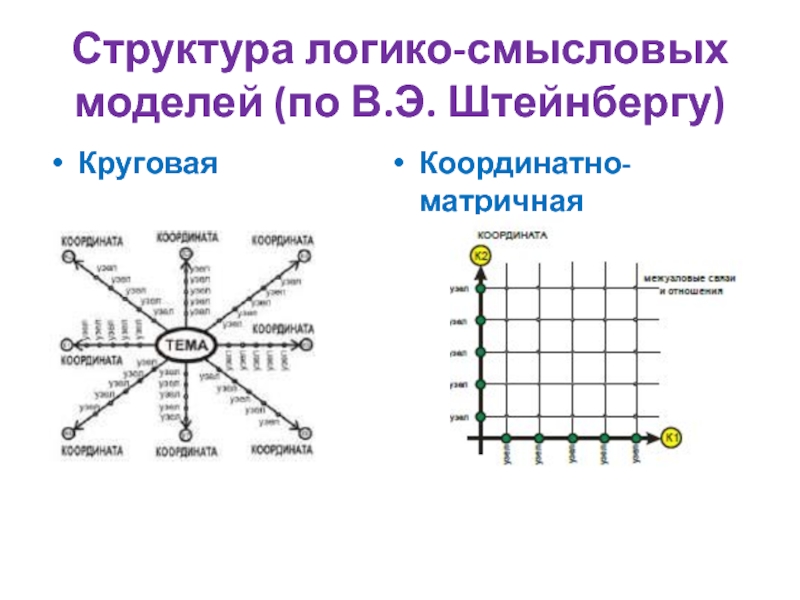
- 14. Структура логико-смысловых моделей (по В.Э. Штейнбергу)Круговая Координатно-матричная
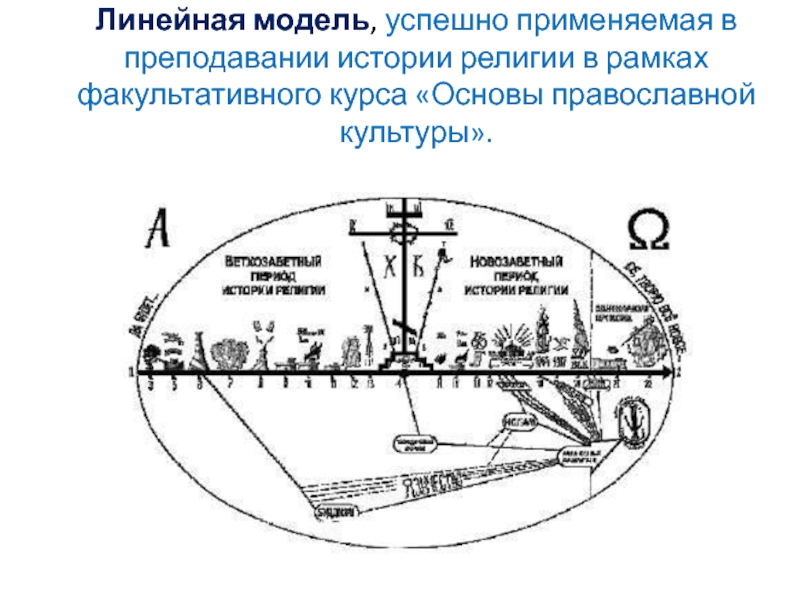
- 15. Линейная модель, успешно применяемая в преподавании истории религии в рамках факультативного курса «Основы православной культуры».
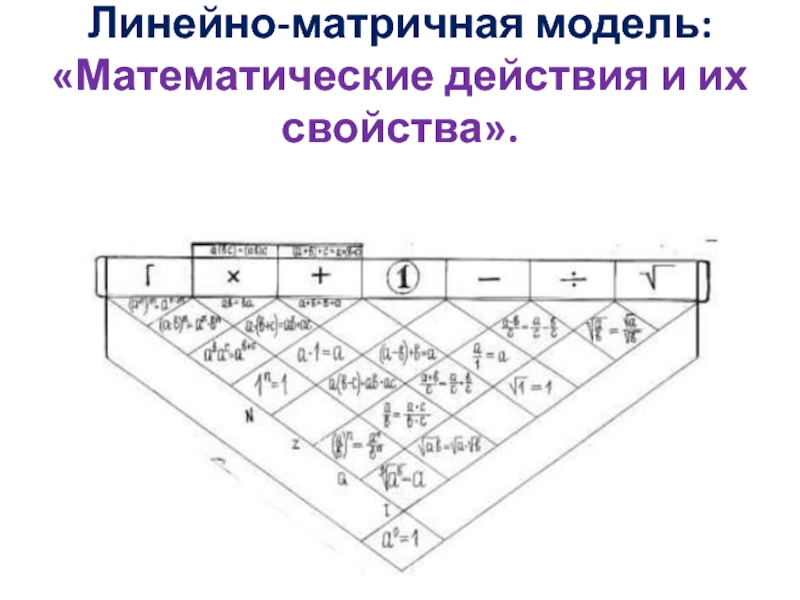
- 16. Линейно-матричная модель: «Математические действия и их свойства».
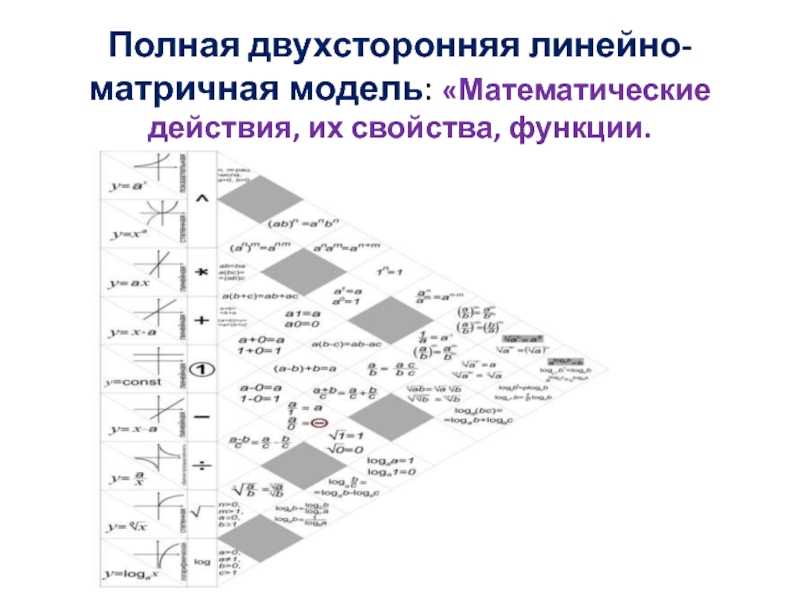
- 17. Полная двухсторонняя линейно-матричная модель: «Математические действия, их свойства, функции.
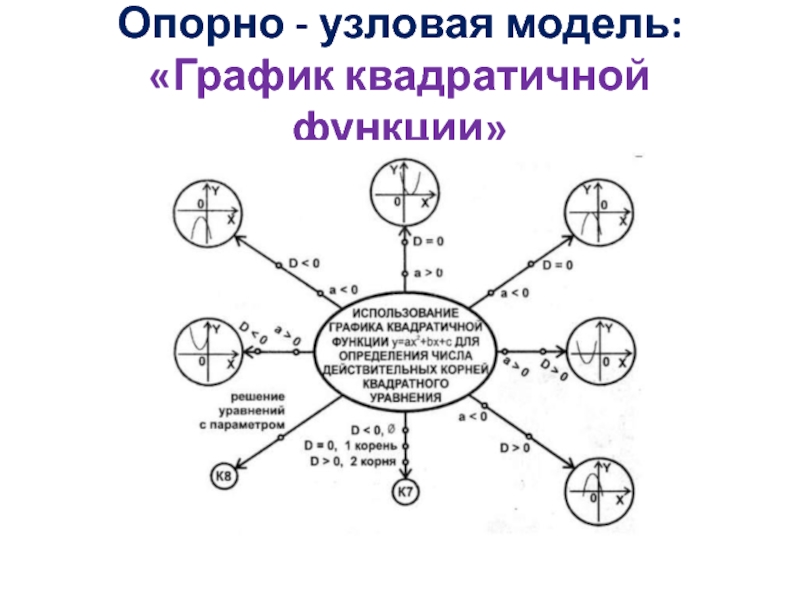
- 18. Опорно - узловая модель: «График квадратичной функции»
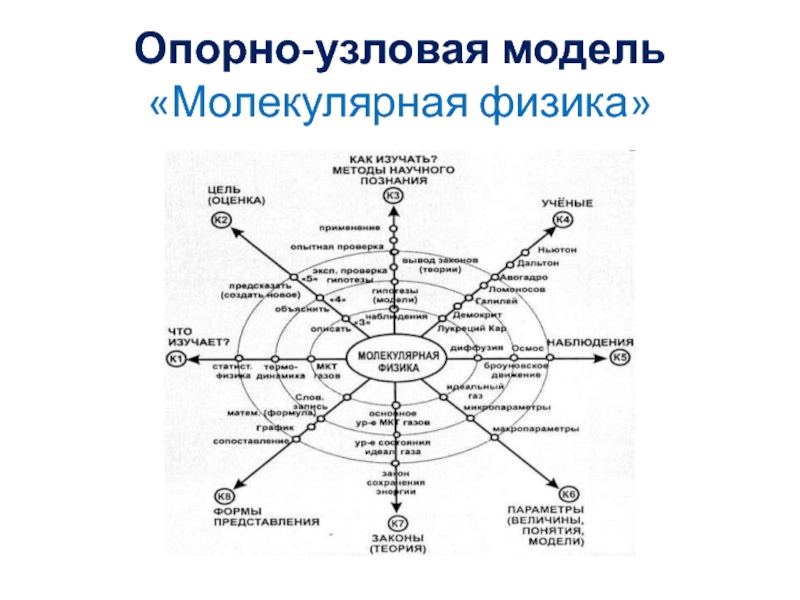
- 19. Опорно-узловая модель «Молекулярная физика»
- 20. Схема многомерной структуры личности
- 21. Таблично-матричные моделиЛогико-смысловая модель «Объѐмы и площади боковых
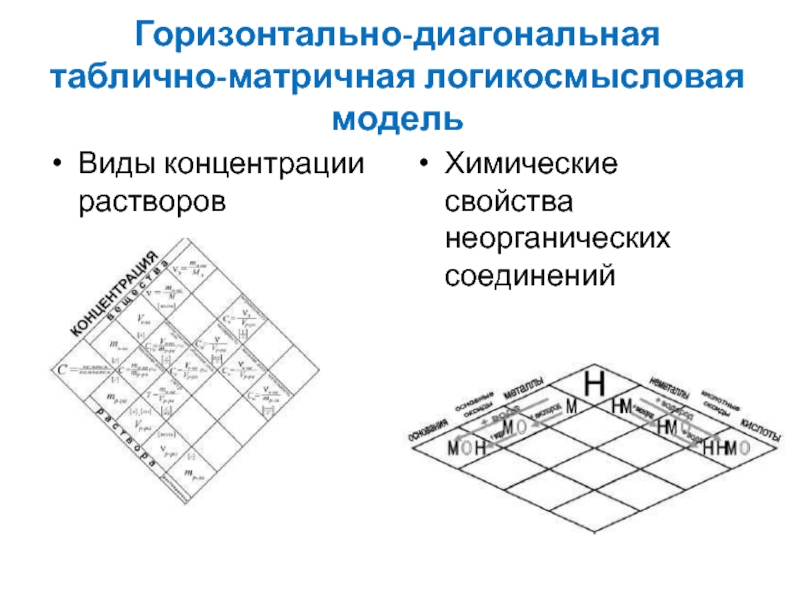
- 22. Горизонтально-диагональная таблично-матричная логикосмысловая модельВиды концентрации растворовХимические свойства неорганических соединений
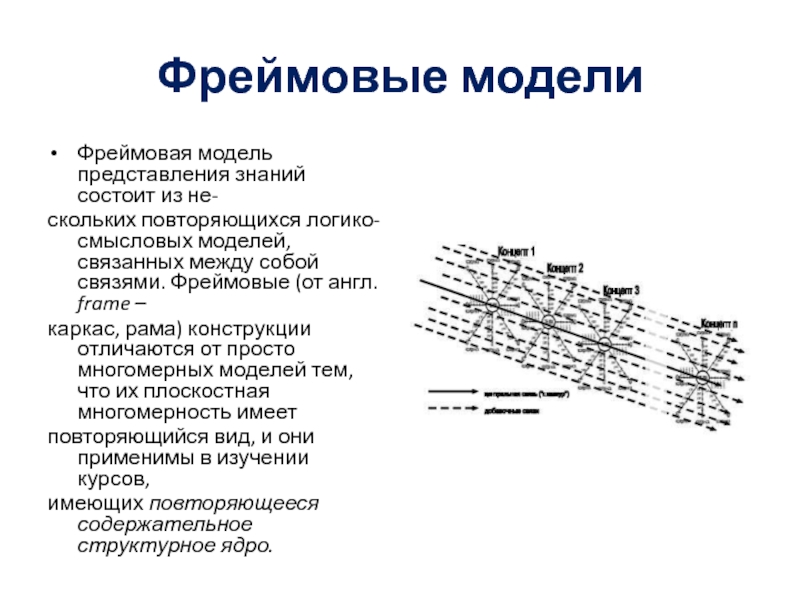
- 23. Фреймовые моделиФреймовая модель представления знаний состоит из
- 24. Фреймовый концепт по теме «Прогрессии»
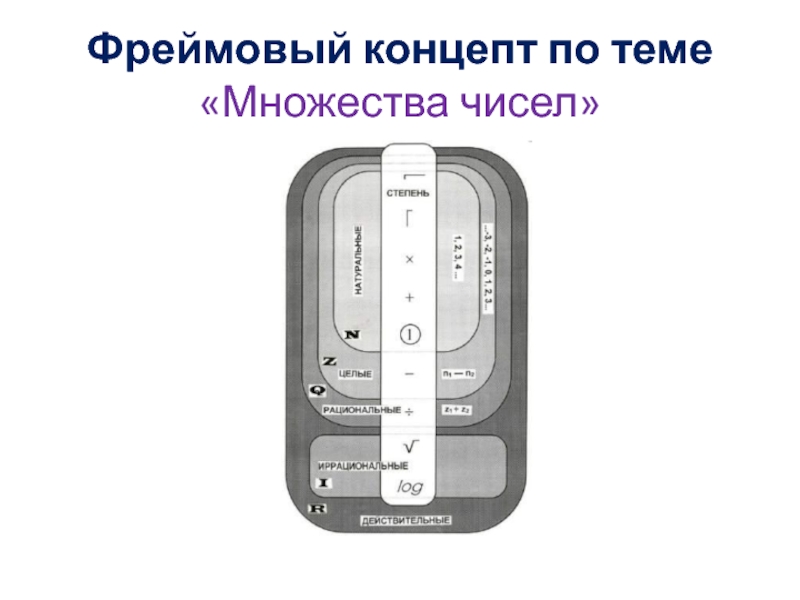
- 25. Фреймовый концепт по теме «Множества чисел»
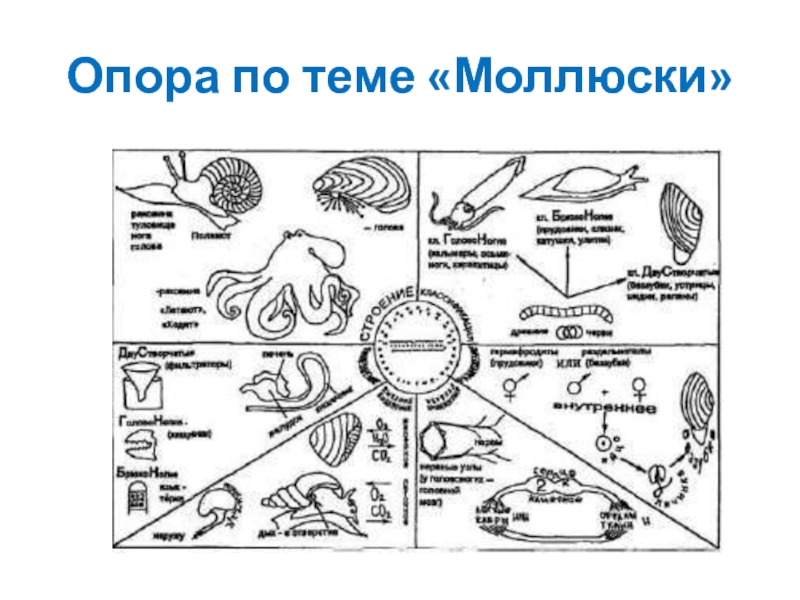
- 26. Опора по теме «Моллюски»
- 27. Классификация крупномодульных структур
- 28. Литература:С.П.Грушевский, А.А. Остапенко «Сгущение учебной информации в профессиональном образовании»МонографияКраснодар 2012
- 29. Скачать презентанцию
«Слепые» схемы «Диффренциальное исчисление».
Слайды и текст этой презентации
Слайд 1Применение приемов сгущения информации
в процессе конструирования
учебных материалов по математике
Учитель математики
Капаева Т.Н.
Слайд 8Миниматрицы - двухмерное табличное графическое изображение закодированных знаний.
В математике -
таблица умножения
Пифагора;
Простейший пример матрицы в химии –
общеизвестнаятаблица растворимости;
* Изучение лиц местоимений в русском языке
Слайд 9Комбинированные элисторы (использованы разные виды кодирования (рисуночный, знаковый, цветовой) и
укрупнения (формула, кратная запись).
«Законы динамики»
«Законы постоянного тока»
Слайд 13(ЛСМ)
Предназначены для того, чтобы представлять и анализировать знания, поддерживать
проектирова-
ние учебного материала, учебного процесса и учебной деятельности».
Анализируя аспект многомерности,
В.Э. Штейнберг выделяет наиболее распространённые в природе, математике и информатике её структуры.Таковыми, по его мнению, являются «солярные» (многолучевые) и «сеточные» (матричные) структуры.
Слайд 15Линейная модель, успешно применяемая в преподавании истории религии в рамках
факультативного курса «Основы православной культуры».
Слайд 17Полная двухсторонняя линейно-матричная модель: «Математические действия, их свойства, функции.
Слайд 21Таблично-матричные модели
Логико-смысловая модель «Объѐмы и площади боковых по-
верхностей
цилиндра, конуса и шара».
Пунктиром на рисунке изображены линии сгиба. Так,
при горизонтальном складывании мы можем изучать толькообъёмы, а при вертикальном – только площади.
Слайд 22Горизонтально-диагональная таблично-матричная логикосмысловая модель
Виды концентрации растворов
Химические свойства неорганических соединений
Слайд 23Фреймовые модели
Фреймовая модель представления знаний состоит из не-
скольких повторяющихся логико-смысловых
моделей, связанных между собой связями. Фреймовые (от англ. frame –
каркас,
рама) конструкции отличаются от просто многомерных моделей тем, что их плоскостная многомерность имеетповторяющийся вид, и они применимы в изучении курсов,
имеющих повторяющееся содержательное структурное ядро.
Слайд 28Литература:
С.П.Грушевский, А.А. Остапенко
«Сгущение учебной информации в профессиональном образовании»
Монография
Краснодар
2012
