Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графы
Содержание
- 1. Графы
- 2. Можно ли объехать станции метро, находящиеся в
- 3. Слайд 3
- 4. ?
- 5. «Графы»
- 6. Топология -наука, которая раньше называлась «геометрией положения».
- 7. Задача Эйлера (1736 г.): «В Кенигсберге река,
- 8. Графом называется … вершины графа – это
- 9. Начертите, не отрывая карандаш от бумаги и
- 10. План:Выяснить признаки фигуры, которую можно нарисовать;Найти начальную точку;Нарисовать всю фигуру
- 11. Не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:
- 12. С чем мы справились?332222222222если нечетных точек в
- 13. Не отрывая карандаша от бумаги и не
- 14. Выводы:1. если нечетных точек в фигуре нет,
- 15. Не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “закрытый конверт”: 33334
- 16. Выводы:1. если нечетных точек в фигуре нет,
- 17. Какие фигуры можно нарисовать одним росчерком?
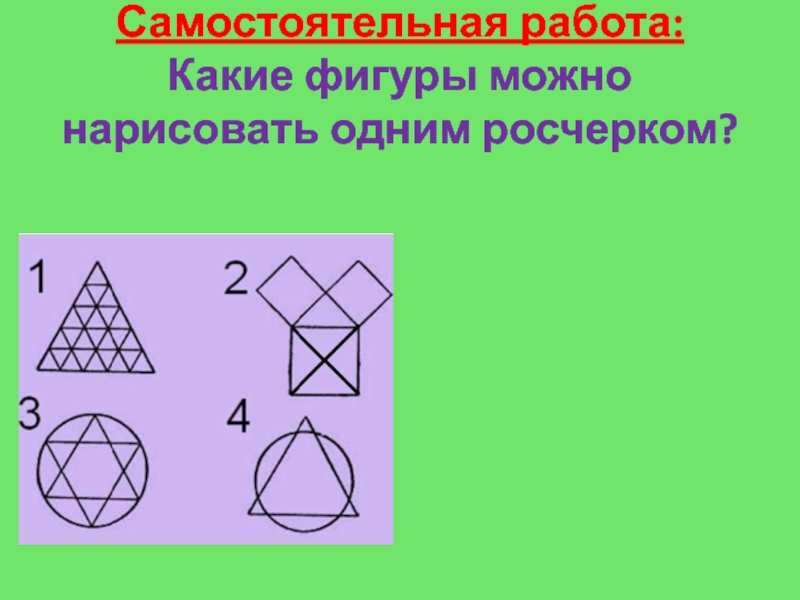
- 18. Самостоятельная работа: Какие фигуры можно нарисовать одним росчерком?
- 19. Самостоятельная работа: Какие фигуры можно нарисовать одним росчерком?Образец:
- 20. Задача Эйлера: «В Кенигсберге река, омывающая два
- 21. Мосты Санкт- ПетербургаЗадача: пройти по 17
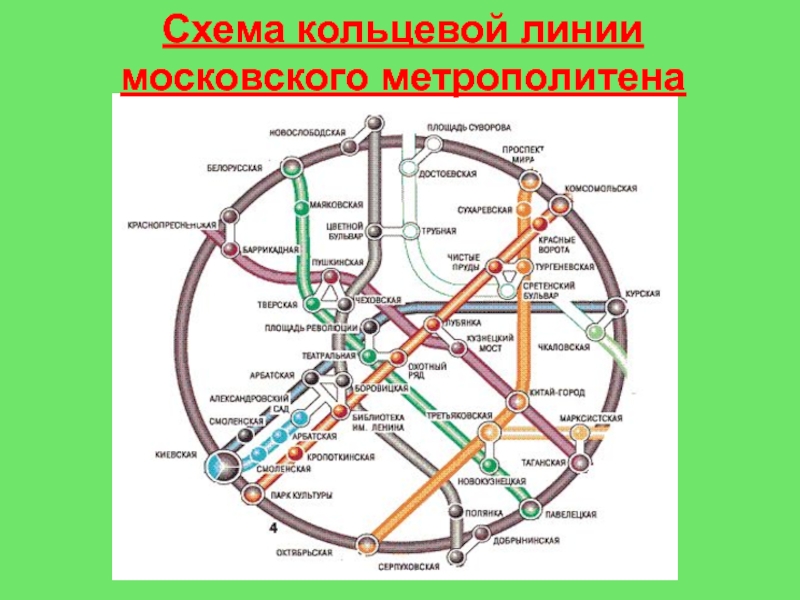
- 22. Схема кольцевой линии московского метрополитена
- 23. Спасибо за внимание! «Мышление начинается с удивления»,-
- 24. Скачать презентанцию
Можно ли объехать станции метро, находящиеся в границе кольцевой линии, лишь один раз посетив каждую из них?
Слайды и текст этой презентации
Слайд 1Тема: «Графы»
Автор:
учитель математики ГБОУ СОШ №1474/1 (2020) г. Москвы
Гусева
Ирина Александровна
Слайд 2Можно ли объехать станции метро, находящиеся в границе кольцевой линии,
лишь один раз посетив каждую из них?
Слайд 6Топология -наука, которая раньше называлась «геометрией положения». Эта отрасль геометрии
занимается только порядком расположения частей фигуры друг относительно друга, отвлекаясь
от их размеровЛеонард Эйлер
(1707-1783)
Разделы топологии:
комбинаторная топология;
алгебраическая топология;
теоретико-множественная топология, изучающую множества как скопления точек.
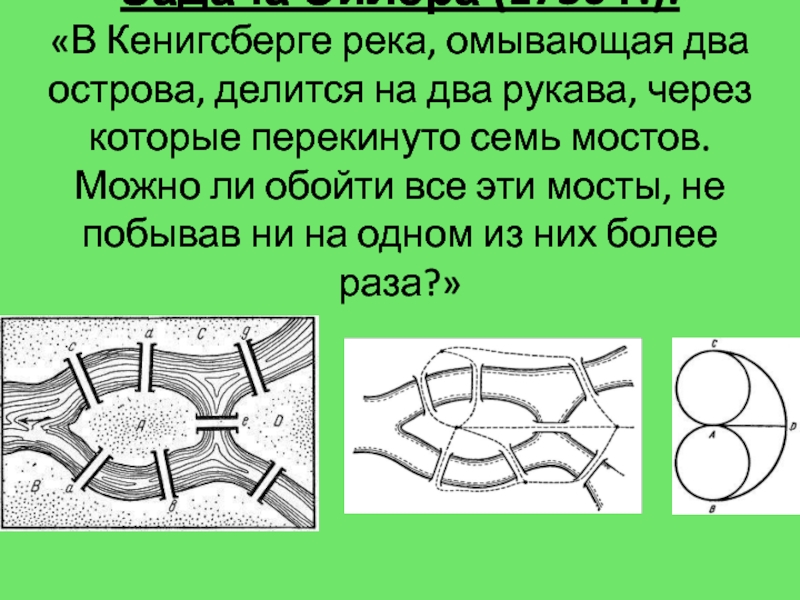
Слайд 7Задача Эйлера (1736 г.): «В Кенигсберге река, омывающая два острова, делится
на два рукава, через которые перекинуто семь мостов. Можно ли
обойти все эти мосты, не побывав ни на одном из них более раза?»
Слайд 8Графом называется …
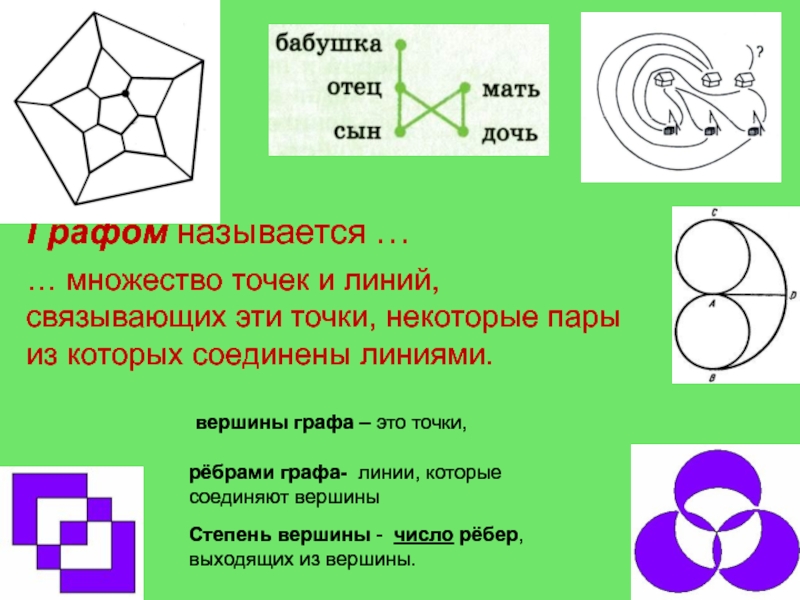
вершины графа – это точки,
рёбрами графа-
линии, которые соединяют вершины
Степень вершины - число рёбер, выходящих
из вершины.… множество точек и линий, связывающих эти точки, некоторые пары из которых соединены линиями.
Слайд 10План:
Выяснить признаки фигуры, которую можно нарисовать;
Найти начальную точку;
Нарисовать всю фигуру
Слайд 11Не отрывая карандаша от бумаги и не проводя по одной
линии дважды, начертить “открытый конверт”:
Слайд 12
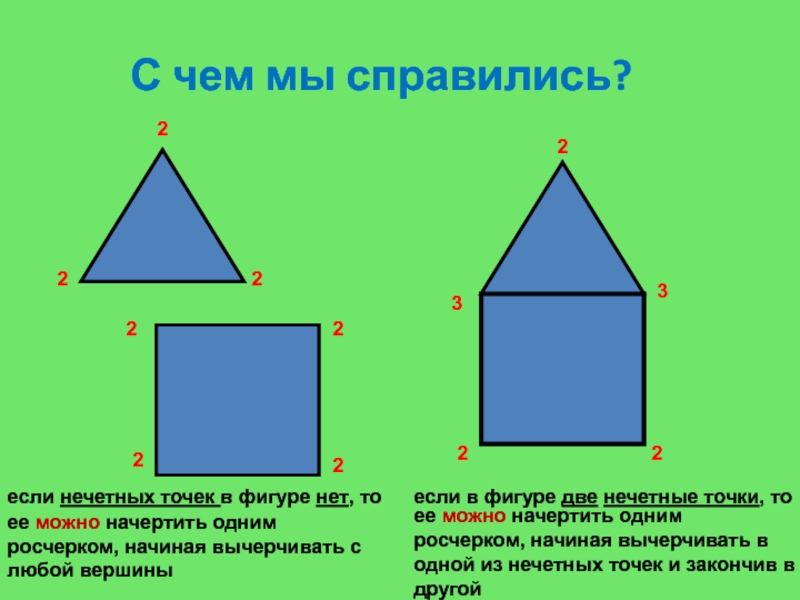
С чем мы справились?
3
3
2
2
2
2
2
2
2
2
2
2
если нечетных точек в фигуре нет, то
ее можно начертить одним росчерком, начиная вычерчивать с любой вершины
если
в фигуре две нечетные точки, то ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой
Слайд 13Не отрывая карандаша от бумаги и не проводя по одной
линии дважды, начертить “открытый конверт”:
2
4
4
4
3
3
Слайд 14Выводы:
1. если нечетных точек в фигуре нет, то ее можно
начертить одним росчерком, начиная вычерчивать с любой вершины.
2. если в
фигуре две нечетные точки, то ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой. 3. если в фигуре больше двух нечетных точек, то ?
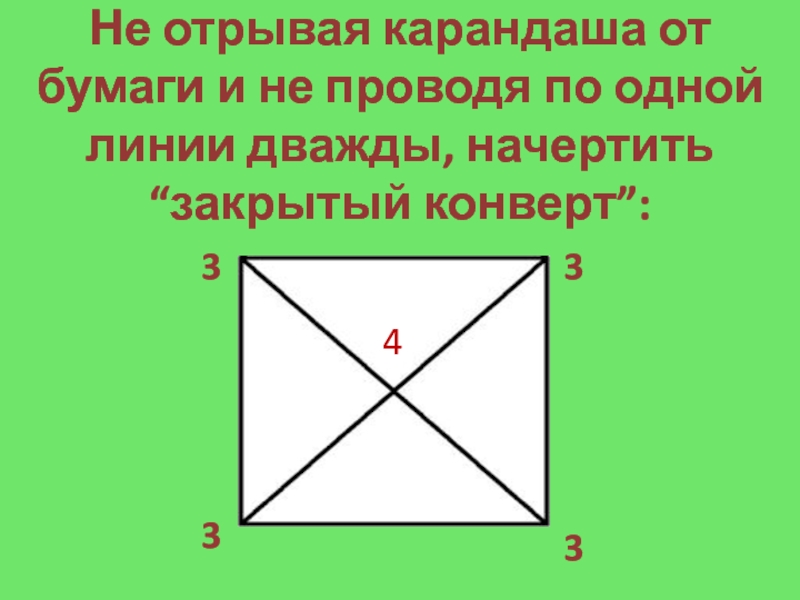
Слайд 15Не отрывая карандаша от бумаги и не проводя по одной
линии дважды, начертить “закрытый конверт”:
3
3
3
3
4
Слайд 16Выводы:
1. если нечетных точек в фигуре нет, то ее можно
начертить одним росчерком, начиная вычерчивать с любой вершины.
2. если в
фигуре две нечетные точки, то ее можно начертить одним росчерком, начиная вычерчивать в одной из нечетных точек и закончив в другой. 3. если в фигуре больше двух нечетных точек, то ее нельзя вычертить одним росчерком.
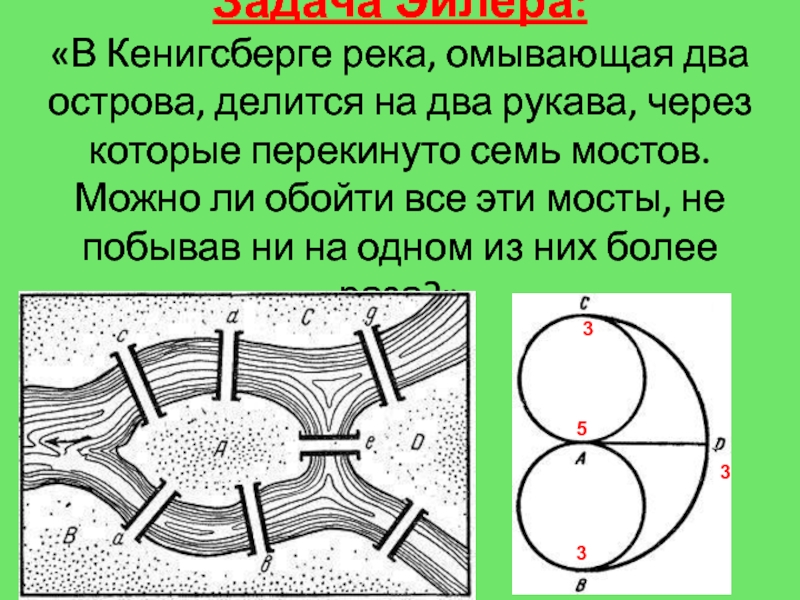
Слайд 20Задача Эйлера: «В Кенигсберге река, омывающая два острова, делится на два
рукава, через которые перекинуто семь мостов. Можно ли обойти все
эти мосты, не побывав ни на одном из них более раза?»3
3
3
5
Слайд 21Мосты
Санкт-
Петербурга
Задача: пройти по 17 мостам, соединяющим участки изображенной здесь
территории Санкт-Петербурга, не побывав ни на одном мосту два раза.
Слайд 23Спасибо за внимание!
«Мышление начинается с удивления»,- заметил 2500 лет
назад Аристотель.
«Чувство удивления – могучий источник желания знать:
от удивления к знаниям – один шаг»Сухомлинский
Математика замечательный предмет для удивления!
