Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интеграл. Формула Ньютона-Лейбница
Содержание
- 1. Интеграл. Формула Ньютона-Лейбница
- 2. Исаак Ньютон Великий английский учёный. Одновременно с
- 3. yyyyxxxx1.4.3.2.На каком рисунке изображена криволинейная трапеция?
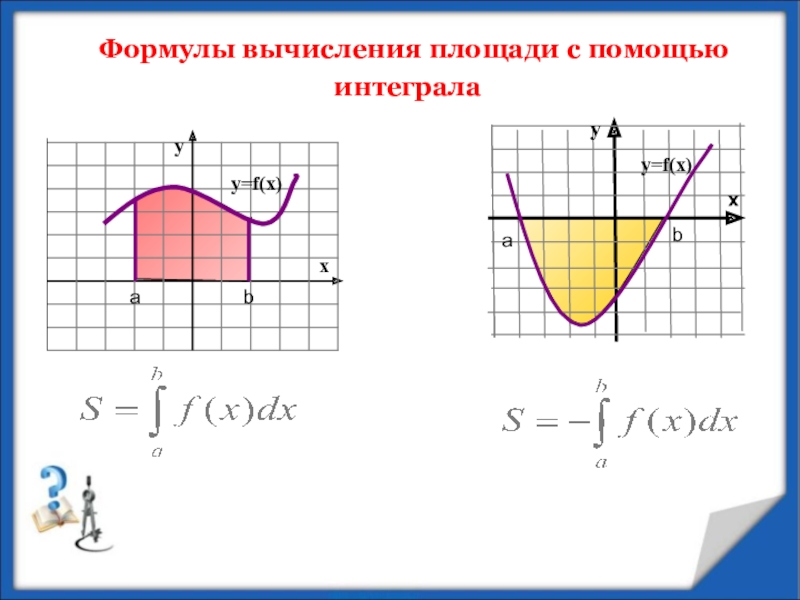
- 4. Формула вычисления площади с помощью интеграла
- 5. ОБ ИНТЕГРАЛЕ МОЖНО СКАЗАТЬ: ИНТЕГРАЛ – ПЛОЩАДЬПлощадь криволинейной
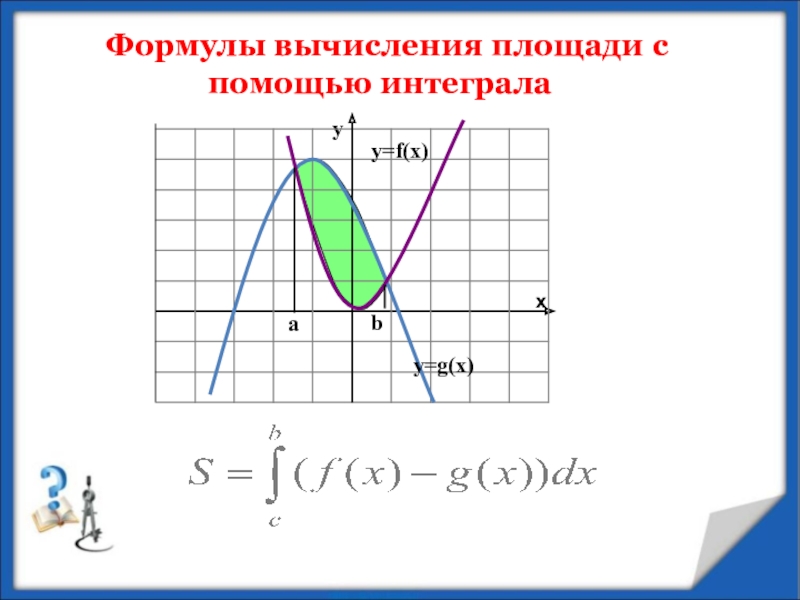
- 6. Формулы вычисления площади с помощью интеграла
- 7. Формулы вычисления площади с помощью интеграла хS= S1+ S2
- 8. Формулы вычисления площади с помощью интеграла x
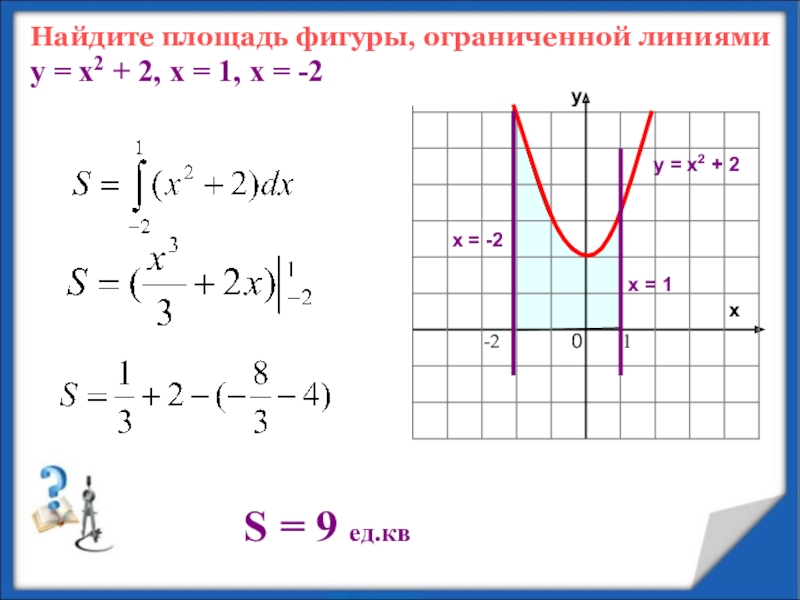
- 9. Найдите площадь фигуры, ограниченной линиями
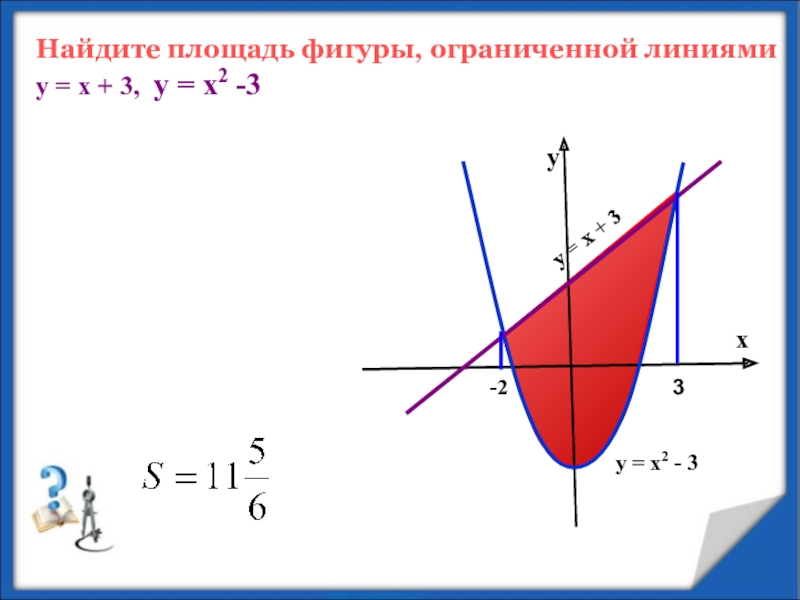
- 10. ху = х2 - 3Найдите площадь фигуры,
- 11. Найдите площадь фигуры, ограниченной линиями
- 12. Еланская ТатьянаСПАСИБО ЗА ВНИМАНИЕ!
- 13. Скачать презентанцию
Исаак Ньютон Великий английский учёный. Одновременно с Лейбницем разработал основы математического анализа. Создатель классической механики. Ньютону принадлежат выдающиеся открытия в оптике, других разделах физики и математики. Главный его труд – «Математические
Слайды и текст этой презентации
Слайд 2Исаак Ньютон
Великий английский учёный. Одновременно с Лейбницем разработал основы математического
Слайд 4Формула вычисления площади с помощью интеграла
Пусть функция
f(x) непрерывна на отрезке [а;b] и пусть F(х) есть какая
– либо её первообразная. Тогда справедливо равенство формула Ньютона-Лейбница
![Формула вычисления площади с помощью интеграла Пусть функция f(x) непрерывна на отрезке [а;b] и пусть](/img/thumbs/1886be14d0fe32b712822045ca594b35-800x.jpg "Интеграл. Формула Ньютона-Лейбница Формула вычисления площади с помощью интеграла Пусть функция f(x) непрерывна")
Слайд 5ОБ ИНТЕГРАЛЕ МОЖНО СКАЗАТЬ:
ИНТЕГРАЛ – ПЛОЩАДЬ
Площадь криволинейной трапеции находится по
формуле
Ньютона-Лейбница
Слайд 11
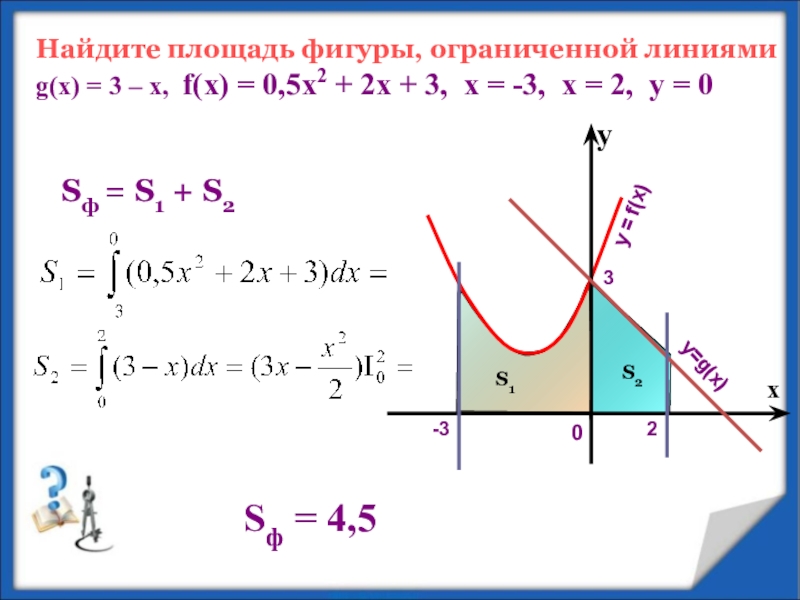
Найдите площадь фигуры, ограниченной линиями
g(x) = 3 –
х, f(x) = 0,5х2 + 2х + 3, х = -3, х = 2, у = 0у
х
S1
S2
Sф = S1 + S2
Sф = 4,5
