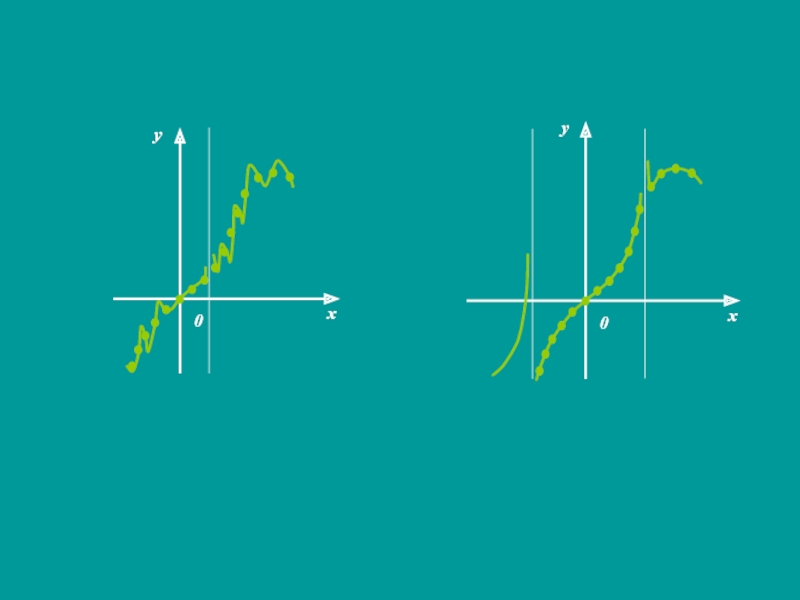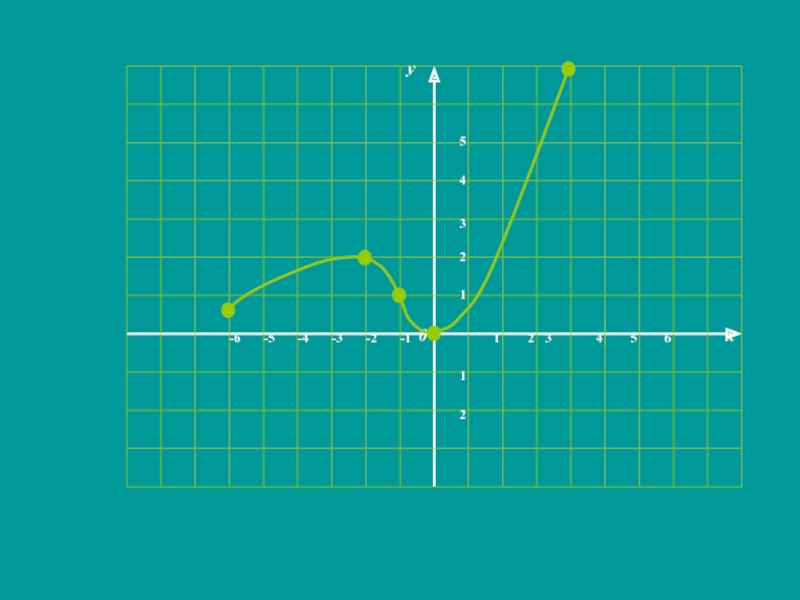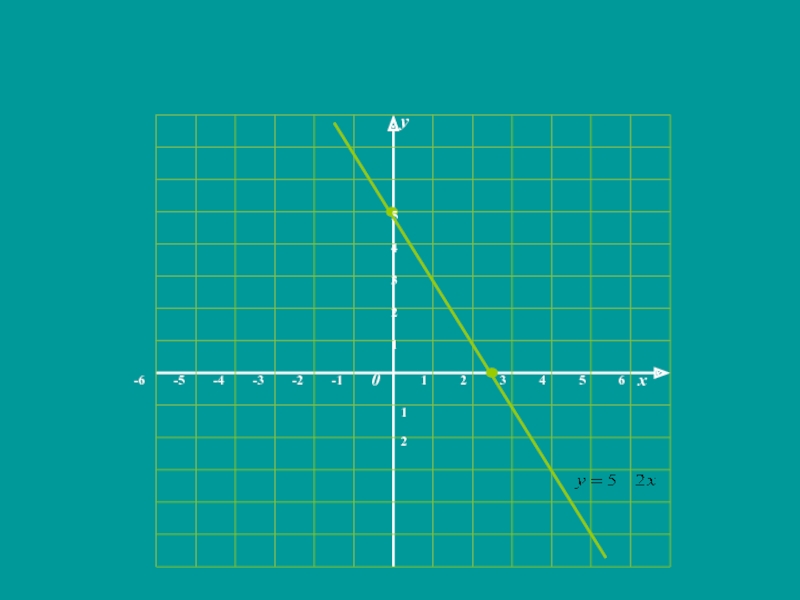Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Исследование функций"
Содержание
- 1. "Исследование функций"
- 2. Цель урока: способствовать развитию навыков чтения графиков и построения графиков функций , используя схему исследования функций.
- 3. Слайд 3
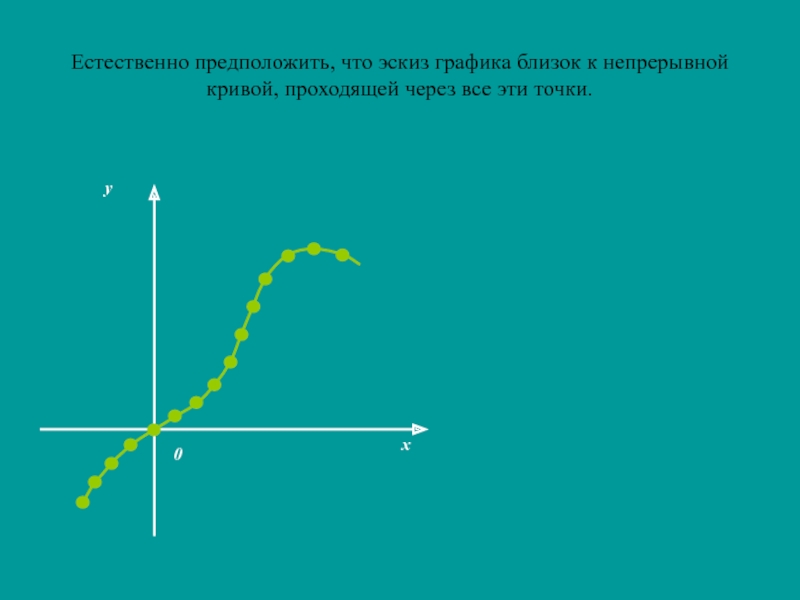
- 4. Естественно предположить, что эскиз графика близок к непрерывной кривой, проходящей через все эти точки.
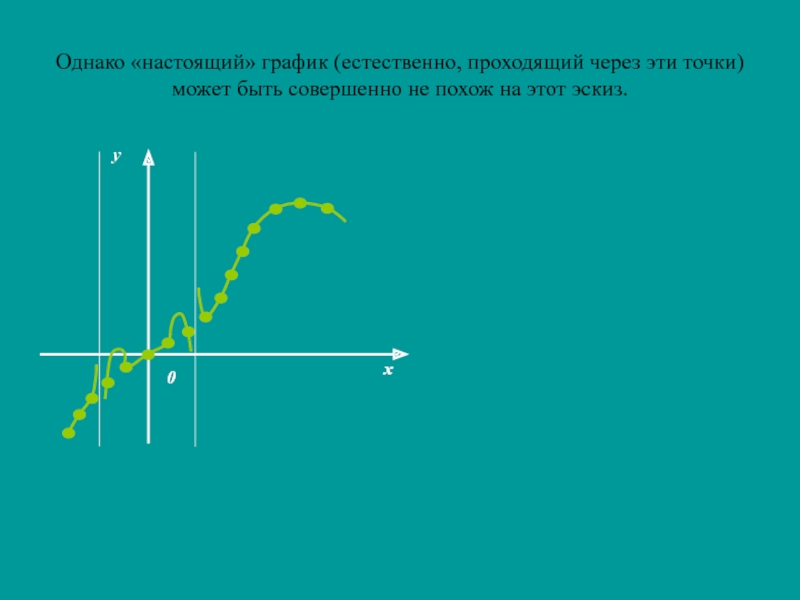
- 5. Однако «настоящий» график (естественно, проходящий через эти точки) может быть совершенно не похож на этот эскиз.
- 6. Слайд 6
- 7. Чтобы избежать ошибок, надо научиться выявлять характерные
- 8. При любом
- 9. Схема исследования функций.1. Найти область определения и
- 10. Графики среднесуточного хода температур по Московской области
- 11. II. Закрепление изученного материала.1.Устно № 93 по рис.57(а,б)Проведите по общей схеме исследование функции, заданной графиком.
- 12. Слайд 12
- 13. 2.№ 94(а; б) Используя приведенные в таблице
- 14. Слайд 14
- 15. Слайд 15
- 16. №95(а).Проведите по общей схеме исследование функции и
- 17. Слайд 17
- 18. III. Домашнее задание:№94(в,г); №95(б;в;г);Стр.290, стр292 №95 и №101.
- 19. Спасибо за внимание.
- 20. Скачать презентанцию
Цель урока: способствовать развитию навыков чтения графиков и построения графиков функций , используя схему исследования функций.
Слайды и текст этой презентации
Слайд 2Цель урока: способствовать развитию навыков чтения графиков и построения графиков
функций , используя схему исследования функций.
Слайд 3
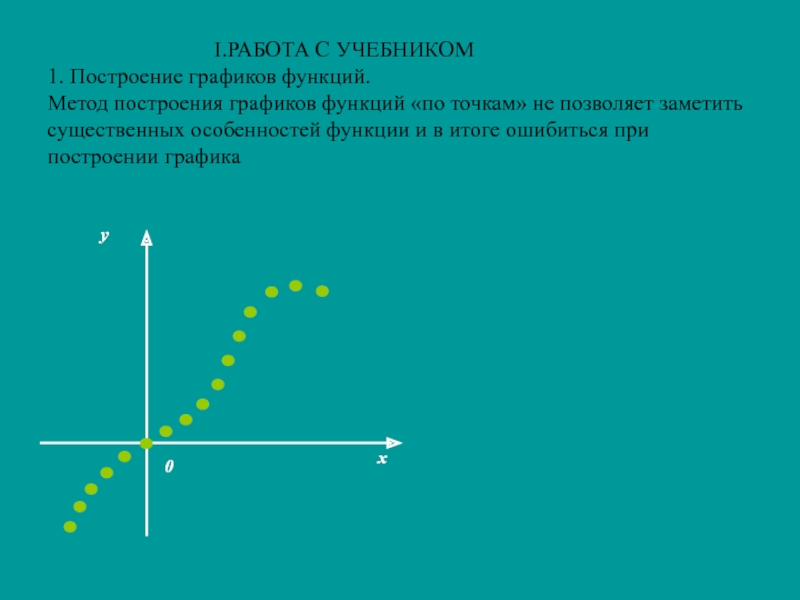
I.РАБОТА С УЧЕБНИКОМ 1. Построение графиков
функций. Метод построения графиков функций «по точкам» не позволяет заметить существенных особенностей функции и в итоге ошибиться при построении графикаСлайд 4Естественно предположить, что эскиз графика близок к непрерывной кривой, проходящей
через все эти точки.
Слайд 5Однако «настоящий» график (естественно, проходящий через эти точки) может быть
совершенно не похож на этот эскиз.
Слайд 7Чтобы избежать ошибок, надо научиться выявлять характерные особенности функции, т.
е. предварительно провести её исследование.
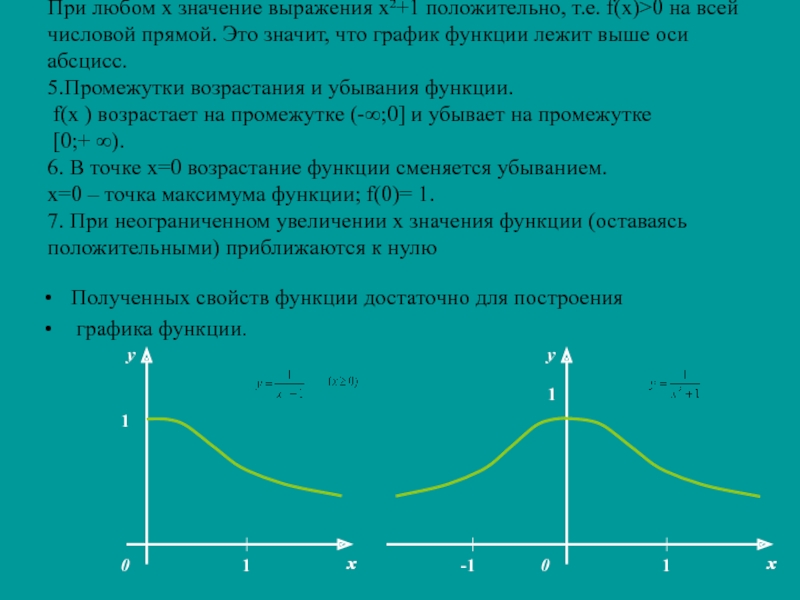
Исследуем функцию
1. Область определения функции вся
числовая прямая, т.к. знаменатель не обращается в нуль.2. Функция чётная, поэтому достаточно исследовать функцию и построить её график при х ≥ 0
3. Точки пересечения с осями координат:
а) с осью ординат (0;1);
б) с осью абсцисс точек пересечения нет, т.к. уравнение f(х)=0
( его корни называют нулями функции) не имеет корней.
4. Найдём промежутки, на которых функция принимает только положительные или только отрицательные значения; их называют промежутками знакопостоянства функции
Слайд 8 При любом х значение выражения х²+1 положительно, т.е. f(х)>0 на
всей числовой прямой. Это значит, что график функции лежит выше
оси абсцисс. 5.Промежутки возрастания и убывания функции. f(х ) возрастает на промежутке (-∞;0] и убывает на промежутке [0;+ ∞). 6. В точке х=0 возрастание функции сменяется убыванием. х=0 – точка максимума функции; f(0)= 1. 7. При неограниченном увеличении х значения функции (оставаясь положительными) приближаются к нулюПолученных свойств функции достаточно для построения
графика функции.
Слайд 9Схема исследования функций.
1. Найти область определения и область значений данной
функции.
2.Выяснить, является ли функция:
а) чётной или нечётной;
б) периодической.
3. Вычислить координаты
точек пересечения графика с осями координат.4. Найти промежутки знакопостоянства функции.
5. Выяснить, на каких промежутках функция возрастает и на каких убывает.
6.Найти точки экстремума, вид экстремума и вычислить значения функции в этих точках.
7. Исследовать поведение функции в окрестности характерных точек и больших ( по модулю) значениях аргумента.
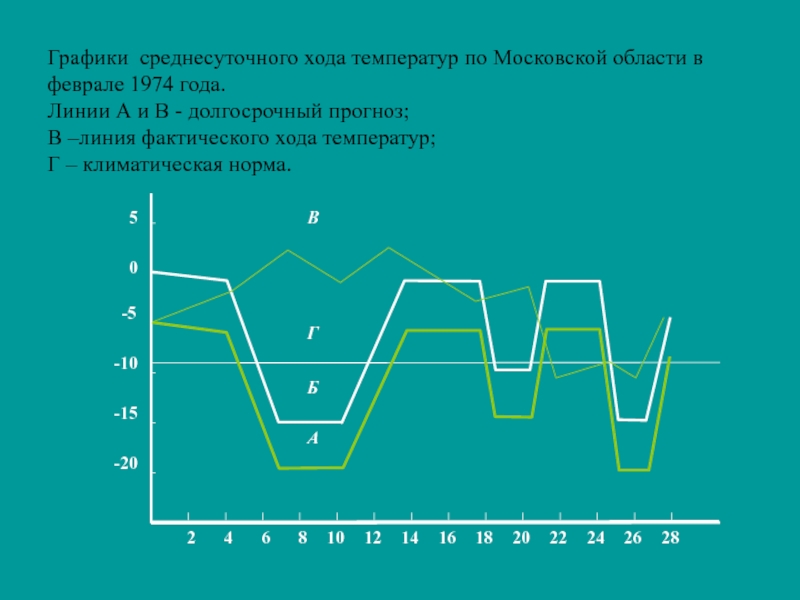
Слайд 10Графики среднесуточного хода температур по Московской области в феврале 1974
года.
Линии А и В - долгосрочный прогноз;
В –линия фактического хода
температур;Г – климатическая норма.
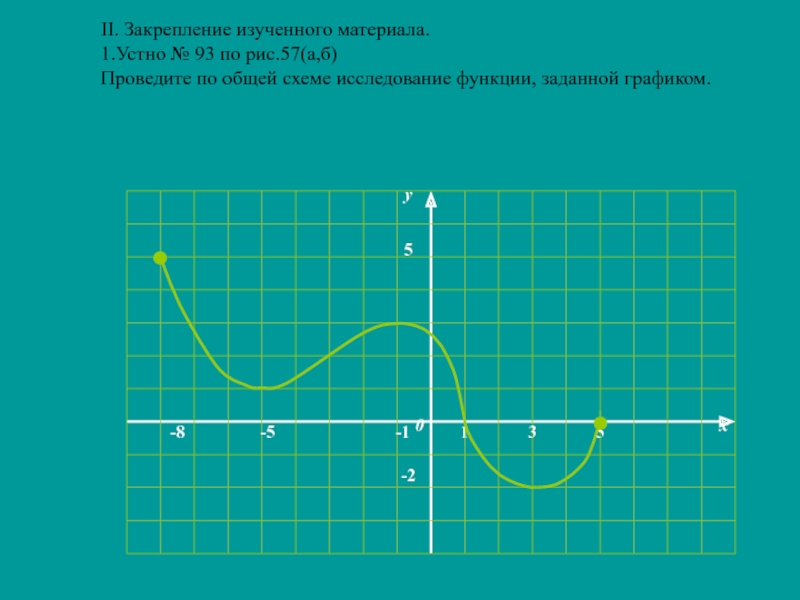
Слайд 11II. Закрепление изученного материала.
1.Устно № 93 по рис.57(а,б)
Проведите по общей
схеме исследование функции, заданной графиком.
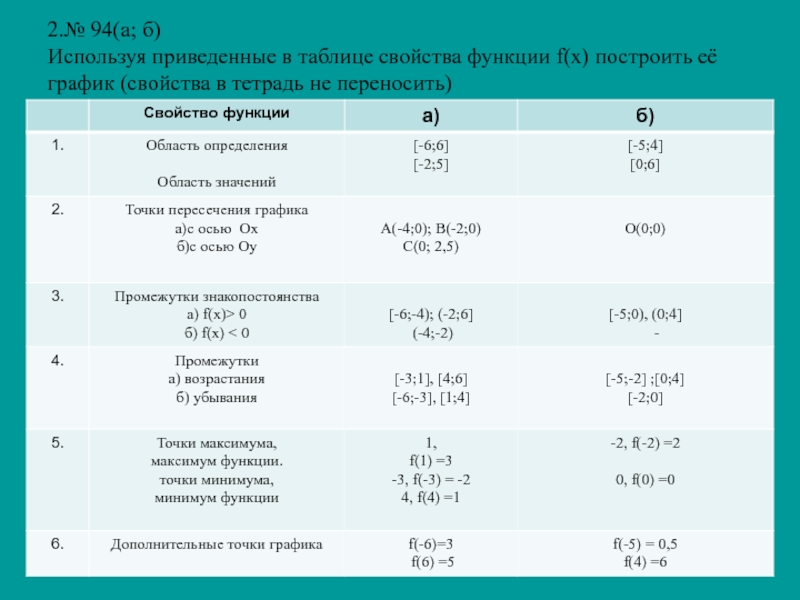
Слайд 132.№ 94(а; б) Используя приведенные в таблице свойства функции f(х) построить
её график (свойства в тетрадь не переносить)
Слайд 16№95(а).Проведите по общей схеме исследование функции и постройте её график f(х)
= 5 – 2х
Решение:
1.D(f) = (-∞;+∞);
2. f(-х)= 5- 2∙ (-х)
=5+ 2х=-(-5 – 2х) – функция ни чётная ни нечётная; непериодическая.3.пересечение с осью Ох:
у = 0; х = 2,5;
пересечение с осью Оу:
х = 0; у = 5.
4. f(х) > 0 при х € (- ∞;2,5)
f(х) < 0 при х € (2,5;+∞)
5.функция убывает на (-∞;+ ∞);
точек экстремума нет;
6.Е(у) =(-∞;+ ∞)