Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование тригонометрических функций
Содержание
- 1. Исследование тригонометрических функций
- 2. СодержаниеОбласть определения функцииОбласть значения функцииПериодичностьПромежутки знакопостоянстваЧетность и нечетность функцийВозрастание и убывание функцийПлан исследования функцииЭкстремумы
- 3. Областью определения функции f(x) называют множество всех
- 4. Задание Найдите область определения функции: ƒ(x)=1+ ctg x ƒ(x)=1+ sin² x ƒ(x)=2cos(x-¶/3)
- 5. Множество, состоящее из всех чисел f(x), таких,
- 6. ЗаданиеНайдите область значений функции: ƒ(x)=3 + 0,5 sin
- 7. Функцию f называют периодической с периодом Т
- 8. ЗаданиеНайдите наименьший положительный период каждой из функций:y=1/2 sin x/4y=4 cos 2xy=3 tg 1,5x
- 9. При каких значениях х функция принимает положительные (отрицательные) значения?f(x)0, если х, принадлежитпромежутку(-П/2+2Пk;П/2+2Пk)
- 10. ЗаданиеНайдите промежутки знакопостоянcтва: y=-sin 3x y=cos x/2 y=tg 2x/3
- 11. График четной функции симметричен относительно оси ординат.
- 12. График нечетной функции симметричен относительно начала координат. (f(-x)=-f(x))На рисункеИзображен график нечетной функции. Достройте графикна промежутке(-П/2;0).
- 13. Функция f возрастает на множестве Р, если
- 14. Функция f убывает на множестве Р, если
- 15. ЗаданиеНайдите промежутки возрастания и убывания функции: y=4 cos 3x y= 2 tg x/2 y= 0,2 sin 4x
- 16. Экстремумы функцииmax f(x): f(П/4+Пk)=1min f(x) определи самостоятельно
- 17. ЗаданиеНайдите экстремумы функции: y=cos (x + ¶/4) y=sin (x + ¶/6) y=1 - sin (x - ¶/3)
- 18. “Чтение” графикаОбласть определения функцииОбласть значений функцииЧетность (нечетность)
- 19. Если что-то не усвоил, вернись на нужную
- 20. Скачать презентанцию
СодержаниеОбласть определения функцииОбласть значения функцииПериодичностьПромежутки знакопостоянстваЧетность и нечетность функцийВозрастание и убывание функцийПлан исследования функцииЭкстремумы
Слайды и текст этой презентации
Слайд 2Содержание
Область определения функции
Область значения функции
Периодичность
Промежутки знакопостоянства
Четность и нечетность функций
Возрастание и
убывание функций
Слайд 3Областью определения функции f(x) называют множество всех значений, которые может
принимать независимая переменная x.
f(x)=2sin x+1
D(f): (- ;+
)f(x)=tg x
D(f): x
Слайд 5Множество, состоящее из всех чисел f(x), таких, что х принадлежит
области определения функции f, называют областью значений функции F.
f(x)=1,5cosx+
E(f)=[-1,5;1,5]
f(x)=tg x
E(f)=(-
;+ )
Слайд 6Задание
Найдите область значений функции:
ƒ(x)=3 + 0,5 sin (x + ¶/4)
ƒ(x)=1,5
– 0,5 cos² x
ƒ(x)=1 + 2 sin x
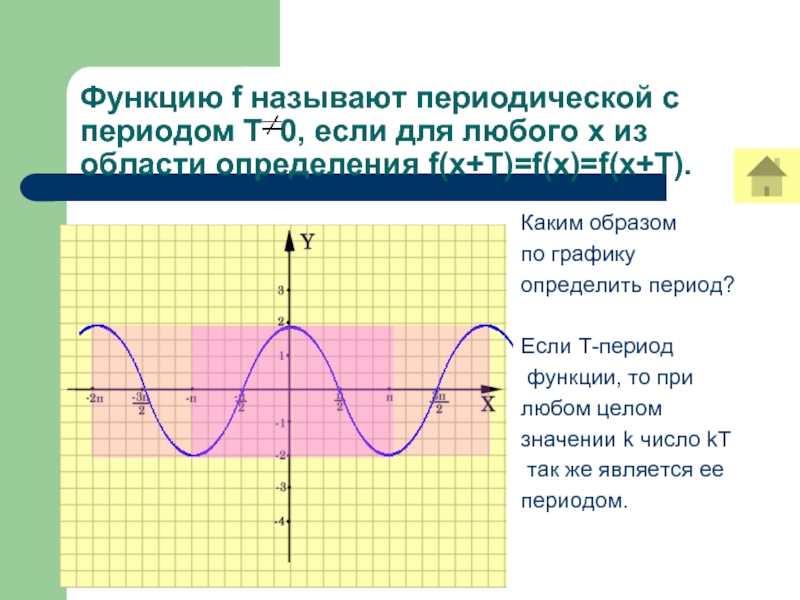
Слайд 7Функцию f называют периодической с периодом Т 0, если для
любого х из области определения f(х+Т)=f(x)=f(x+T).
Каким образом
по графику
определить период?
Если
Т-периодфункции, то при
любом целом
значении k число kT
так же является ее
периодом.
Слайд 8Задание
Найдите наименьший положительный период каждой из функций:
y=1/2 sin x/4
y=4 cos
2x
y=3 tg 1,5x
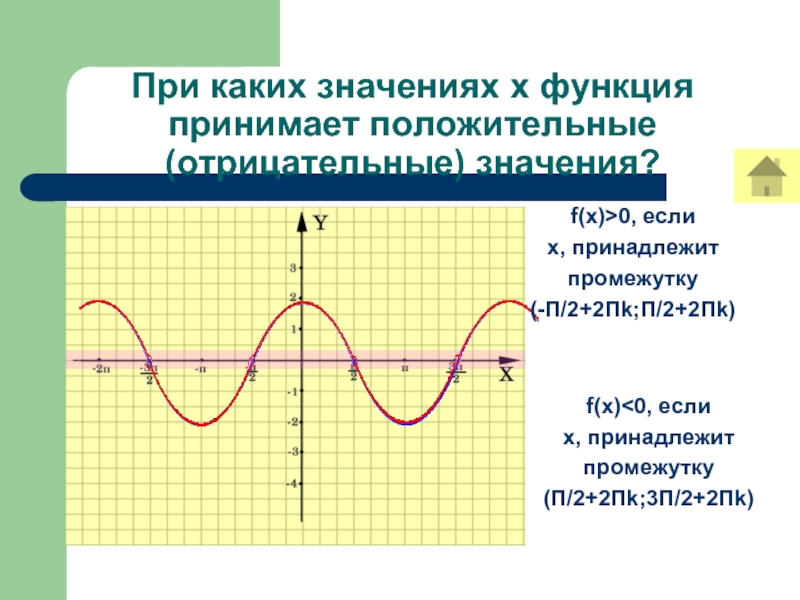
Слайд 9При каких значениях х функция принимает положительные (отрицательные) значения?
f(x)
принадлежит
промежутку
(П/2+2Пk;3П/2+2Пk)
f(x)>0, если
х, принадлежит
промежутку
(-П/2+2Пk;П/2+2Пk)
Слайд 11График четной функции симметричен относительно оси ординат.
(f(-x)=f(x))
На рисунке
изображен график
четной
функции.
Достройте график
на промежутке
(-П/2;0).
График какой
функции
получился?
f(x)=2sin|x|
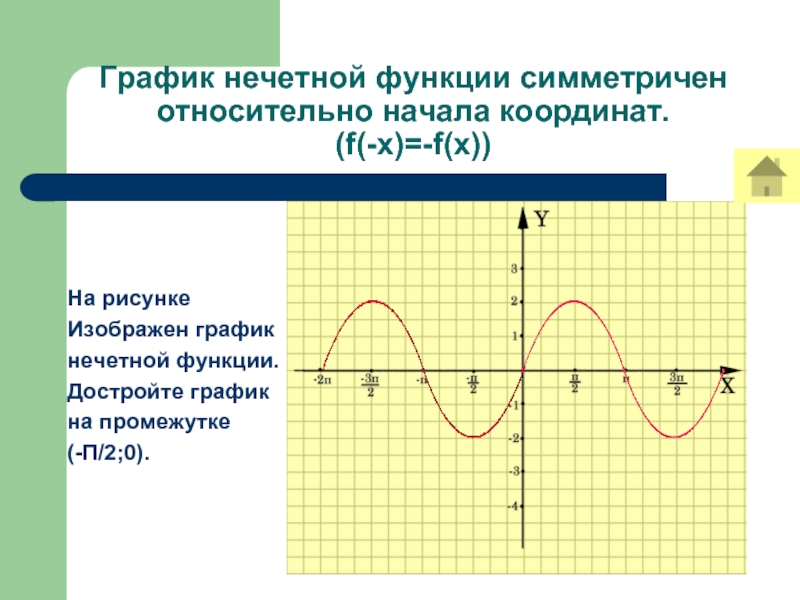
Слайд 12График нечетной функции симметричен относительно начала координат.
(f(-x)=-f(x))
На рисунке
Изображен график
нечетной
функции.
Достройте график
на промежутке
(-П/2;0).
Слайд 13Функция f возрастает на множестве Р, если для любых х1
и х2 из множества Р, таких, что х1>х2, выполнено неравенство
f(x1)>f(x2).Определите
промежутки
возрастания
функции.
[Пk;3П/2k]
f(x)=-cosx
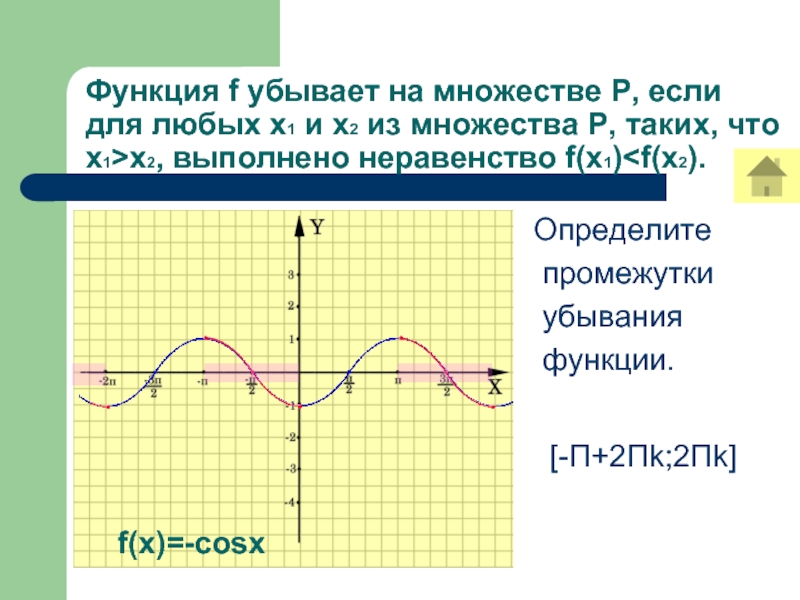
Слайд 14Функция f убывает на множестве Р, если для любых х1
и х2 из множества Р, таких, что х1>х2, выполнено неравенство
f(x1)Определите
промежутки
убывания
функции.
[-П+2Пk;2Пk]
f(x)=-cosx
Слайд 15Задание
Найдите промежутки возрастания и убывания функции:
y=4 cos 3x
y= 2 tg
x/2
y= 0,2 sin 4x
Слайд 18“Чтение” графика
Область определения функции
Область значений функции
Четность (нечетность) функции
Периодичность (наименьший положительный
период) функции
Точки пересечения графика с осями
Промежутки знакопостоянства
Промежутки возрастания (убывания) функции
Максимумы
(минимумы)
Слайд 19Если что-то не усвоил, вернись на нужную страницу.
Область определения функции
Область
значения функции
Периодичность
Промежутки знакопостоянства
Четность и нечетность функций
Возрастание и убывание функций
Максимумы (минимумы)
План
исследования функции
Теги
