Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Содержание
- 1. Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
- 2. Вводная беседаГеометрия в переводе с греческого«землемерие» («гео»-
- 3. Вводная беседаНаибольшее влияние на все последующее развитие
- 4. Вводная беседаШкольный курс геометрии делится на планиметрию
- 5. Вводная беседаВ геометрии изучаются формы, размеры, взаимное
- 6. СодержаниеПонятие прямойСвойства прямойОтрезокЛучУголСамостоятельная работа
- 7. Понятие прямойПостройте две пары точек. Итог:Линейка -
- 8. Свойства прямойПостройте две точки А и В,
- 9. Свойства прямойВопрос:Как далеко уходит прямая АВ влево? Вправо? Замкнута ли прямая?АВВстретятся ли крокодил и пчела?
- 10. Свойства прямой1. Через две различные точки проходит
- 11. ОтрезокПостройте прямую АВ и точки М и
- 12. Решение задачЗадача № 5a Проведите
- 13. Решение задачЗадача № 7А) отрезки АС, ВС,
- 14. ЛучПостройте прямую АВ, точку О, О
- 15. Решение задачЗадача № 8А) ВА и ВС,
- 16. УголПостройте два различных луча ОА и ОВОАВОкажутся
- 17. Решение задачПоставьте знак или :C… MNKD… MNKB… MNK
- 18. 1. Постройте два угла так, чтобы их пересечением был угол.Решение задач2. Найдите решение.
- 19. Решение задачПостройте два угла так, чтобы их
- 20. Самостоятельная работаПо рисунку 1 ответьте на вопросы:1.
- 21. Проверь себя!1. AB, BD, AD, DC, BC,
- 22. Домашнее заданиеПункты 1, 3, 4 читать, выучить введенные понятия, № 2, 6, 10, 16.
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1«Начальные понятия планиметрии. Прямая и отрезок. Луч и угол»
Разработка урока
по геометрии 7 класса
Слайд 2Вводная беседа
Геометрия в переводе с греческого
«землемерие»
(«гео»- по-гречески земля, а
«метрео» - мерить)
Первым, кто начал получать геометрические факты при помощи
рассуждений (доказательств), был древнегреческий математик Фалес (6 в. до н. э.), который в своих исследованиях применял перегибание чертежа, поворот части фигуры и так далее, то есть то, что на современном геометрическом языке называется движением.Слайд 3Вводная беседа
Наибольшее влияние на все последующее развитие геометрии оказали труды
греческого ученого Евклида, жившего в Александрии в 3 в. до
н. э.Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой изучали геометрию. В «Началах» были систематизированы известные к тому времени геометрические сведения, и геометрия впервые предстала как математическая наука.
Слайд 4Вводная беседа
Школьный курс геометрии делится на планиметрию и стереометрию.
Раздел
геометрии, изучающий свойства фигур на плоскости, называется планиметрией (от латинского
слова «планум» - плоскость и греческого «метрео» - измеряю).В стереометрии изучаются свойства фигур в пространстве, таких как параллелепипед, шар, цилиндр, пирамида.
Слайд 5Вводная беседа
В геометрии изучаются формы, размеры, взаимное расположение предметов независимо
от их других свойств: массы, цвета и т. д. Отвлекаясь
от этих свойств и беря во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.На уроках математики вы познакомились с некоторыми геометрическими фигурами и представляете себе, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга.
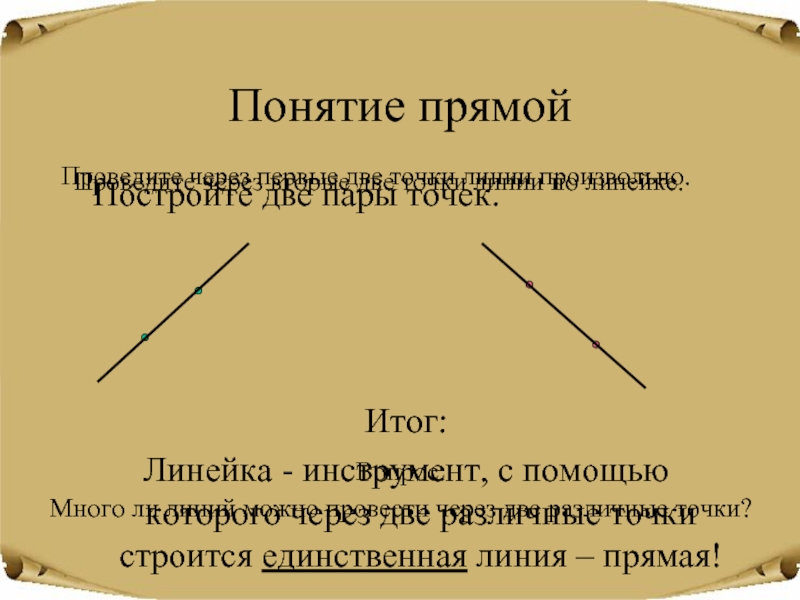
Слайд 7Понятие прямой
Постройте две пары точек.
Итог:
Линейка - инструмент, с помощью
которого через две различные точки строится единственная линия – прямая!
Проведите
через первые две точки линии произвольно.Проведите через вторые две точки линии по линейке.
Вопрос:
Много ли линий можно провести через две различные точки?
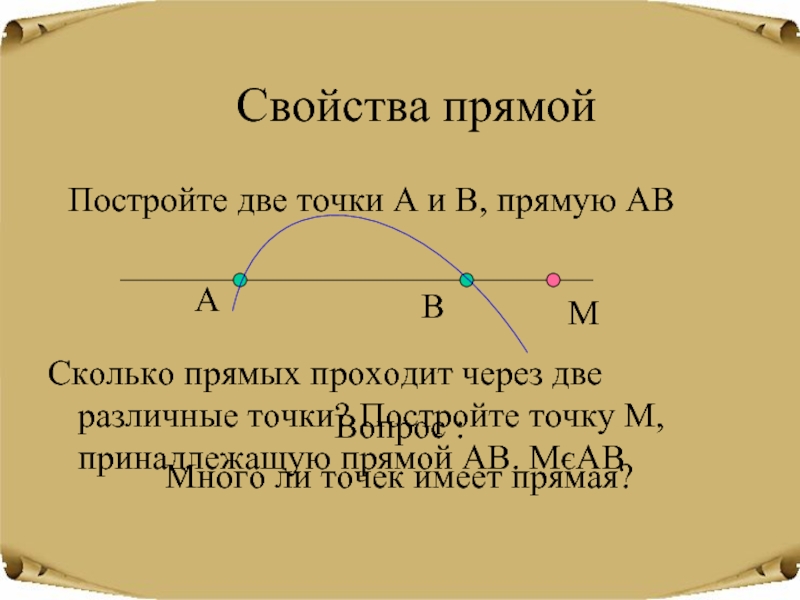
Слайд 8Свойства прямой
Постройте две точки А и В, прямую АВ
А
В
Сколько прямых
проходит через две различные точки? Постройте точку М, принадлежащую прямой
АВ. МєАВМ
Вопрос :
Много ли точек имеет прямая?
Слайд 9Свойства прямой
Вопрос:
Как далеко уходит прямая АВ влево? Вправо?
Замкнута ли
прямая?
А
В
Встретятся ли крокодил и пчела?
Слайд 10Свойства прямой
1. Через две различные точки проходит единственная прямая.
2. Прямая
имеет бесконечно много точек.
3. Прямая бесконечна.
4. Прямая незамкнута.
5. Прямая делит
плоскость на двеполуплоскости
Слайд 11Отрезок
Постройте прямую АВ и точки М и К, М
АВ, К АВ
М
К
Если объединить две точки прямой и все
точки между ними, то получим отрезок.Отрезок МК.
Измерьте длину отрезка МК : МК=
Слайд 12Решение задач
Задача № 5
a
Проведите прямую а и
отметьте на ней точки А и В. Отметьте: а) точки
М и N, лежащие на отрезке АВ; б) точки P и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.Слайд 13Решение задач
Задача № 7
А) отрезки АС, ВС, СD, BD, AD.
Б)
отрезок CD.
На рисунке изображена прямая, на ней отмечены точки А,
В, С и D. Назовите все отрезки : а) на которых лежит точка С. Б) на которых не лежит точка В.
Слайд 14Луч
Постройте прямую АВ, точку О, О АВ
А
О
В
Если точку объединить
с одной из частей, на которые она разделила прямую, то
получим луч. Луч ОВ.
Луч ОА
Точка О – начало луча
Слайд 15Решение задач
Задача № 8
А) ВА и ВС,
АС и АВ.
Б) СВ.
Проведите прямую, отметьте
на ней точки А и В и на отрезке АВ отметьте точку С. А) Среди лучей АВ, ВС, СА, АС и ВА найдите пары совпадающих лучей.
Б) назовите луч, который является продолжением луча СА.
Слайд 16Угол
Постройте два различных луча ОА и ОВ
О
А
В
Окажутся ли вместе кошка
и рыбка, если нельзя переходить лучи?
Если два луча, имеющие общее
начало, объединить с одной из областей, на которые они делят плоскость, то получим угол. AOB или BOA
Слайд 19Решение задач
Постройте два угла так, чтобы их пересечением был луч.
Постройте
два угла так, чтобы их пересечением был отрезок.
Решение ли это?
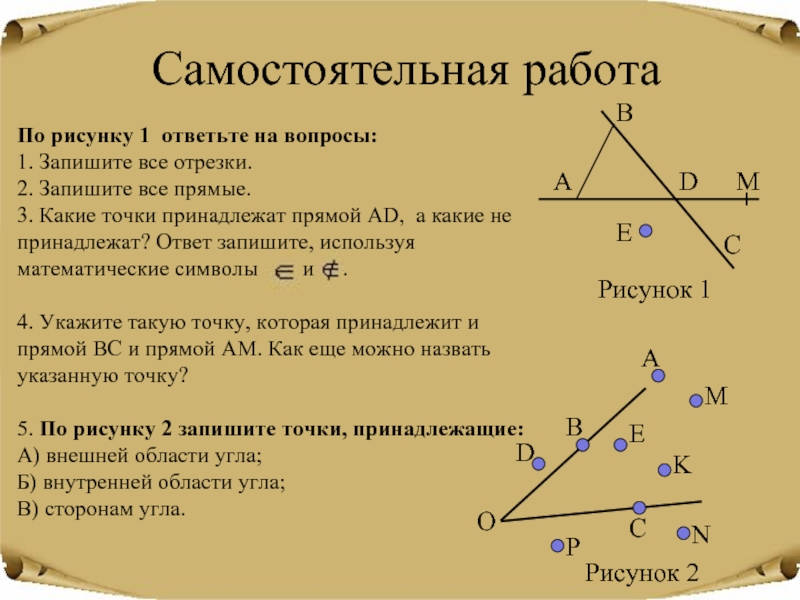
Слайд 20Самостоятельная работа
По рисунку 1 ответьте на вопросы:
1. Запишите все отрезки.
2.
Запишите все прямые.
3. Какие точки принадлежат прямой AD, а какие
не принадлежат? Ответ запишите, используя математические символы и .4. Укажите такую точку, которая принадлежит и прямой ВС и прямой АМ. Как еще можно назвать указанную точку?
5. По рисунку 2 запишите точки, принадлежащие:
А) внешней области угла;
Б) внутренней области угла;
В) сторонам угла.
О
D
B
A
E
M
K
C
P
N
Рисунок 2
A
B
D
M
C
E
Рисунок 1
Слайд 21Проверь себя!
1. AB, BD, AD, DC, BC, DM, AM.
2. AМ,
BC.
3. A AD, D AD,
M AD, B AD, E AD, C AD.
4. D, точка пересечения прямых ВС и АМ.
5. А) D, P, N
Б) E, K, M
В) A, B, O, C