Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Касательная к параболе. Оптическое свойство параболы.
Содержание
- 1. Касательная к параболе. Оптическое свойство параболы.
- 2. ПараболаПара́бола (греч. Παραβολή - приложение) — геометрическое место точек,
- 3. Касательная к параболеОпределение. Прямая, имеющая с параболой
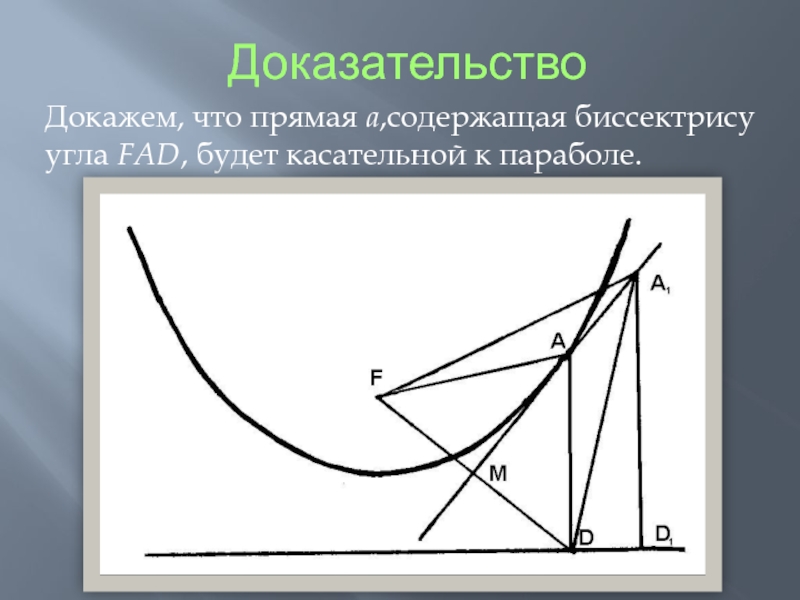
- 4. ДоказательствоДокажем, что прямая a,содержащая биссектрису угла FAD, будет касательной к параболе.
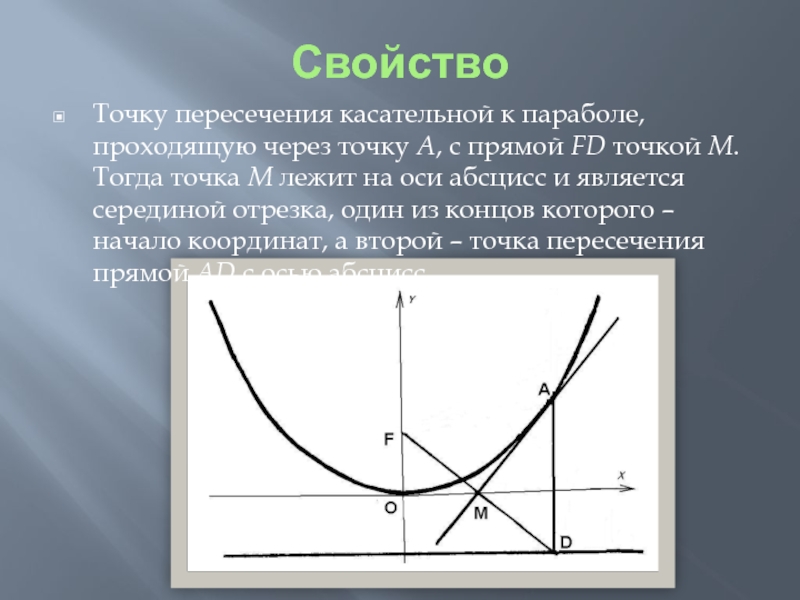
- 5. СвойствоТочку пересечения касательной к параболе, проходящую через
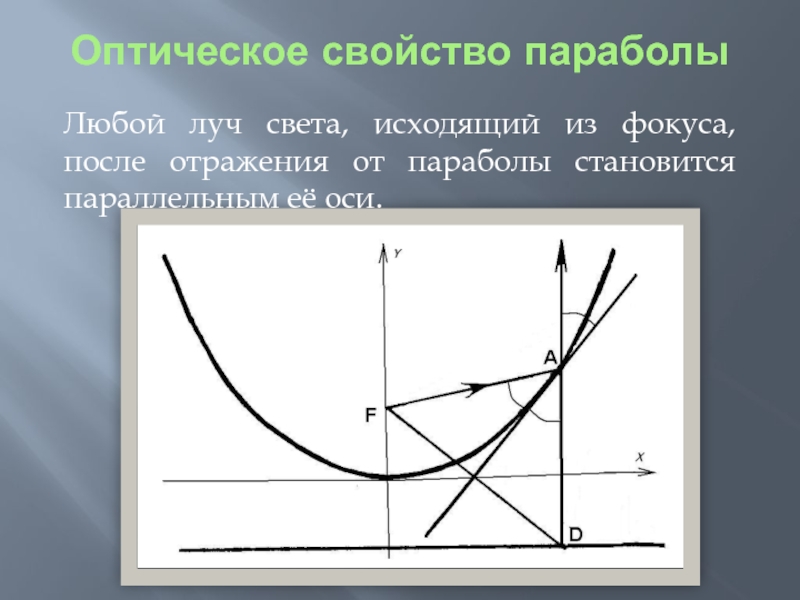
- 6. Оптическое свойство параболы Любой луч света, исходящий
- 7. Применение оптического свойства параболы
- 8. Скачать презентанцию
ПараболаПара́бола (греч. Παραβολή - приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы)
Слайды и текст этой презентации
Слайд 1Касательная к параболе.
Оптическое свойство параболы
Учитель математики
ГОУ РК «ФМЛИ»
Рубцова О.М.
Слайд 2Парабола
Пара́бола
(греч. Παραβολή - приложение) —
геометрическое место точек, равноудалённых от данной
прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы)
Слайд 3Касательная к параболе
Определение. Прямая, имеющая с параболой только одну общую
точку и не перпендикулярная её директрисе, называется касательной к параболе.
Теорема.
Пусть A – точка на параболе с фокусом F и директрисой d, AD – перпендикуляр, опущенный на директрису. Тогда касательная к параболе, проведенная через точку А будет прямая, содержащая биссектрису угла FAD. 
Слайд 4Доказательство
Докажем, что прямая a,содержащая биссектрису угла FAD, будет касательной к
параболе.
Слайд 5Свойство
Точку пересечения касательной к параболе, проходящую через точку А, с
прямой FD точкой М. Тогда точка М лежит на оси
абсцисс и является серединой отрезка, один из концов которого – начало координат, а второй – точка пересечения прямой AD с осью абсцисс
Слайд 6Оптическое свойство параболы
Любой луч света, исходящий из фокуса, после отражения
от параболы становится параллельным её оси.
