Пифагор Самосский

= 1,35   
Ф 0,6156:1,9= 0,324 
И 121,4-29,7= 91,7 
 П 132,96+21,4 =154,36 
 А

(8,75+3,6) *6,9= 85,215 
 Р 7,04:5 +5,624:9,5 = 2
 О (11,76-9,36)*0,5051, =1,21224   1,212
 
154,36     91,7     0,324    85,215     1,35      1,212      2
П и ф а г о р

Что открыл Пифагор?

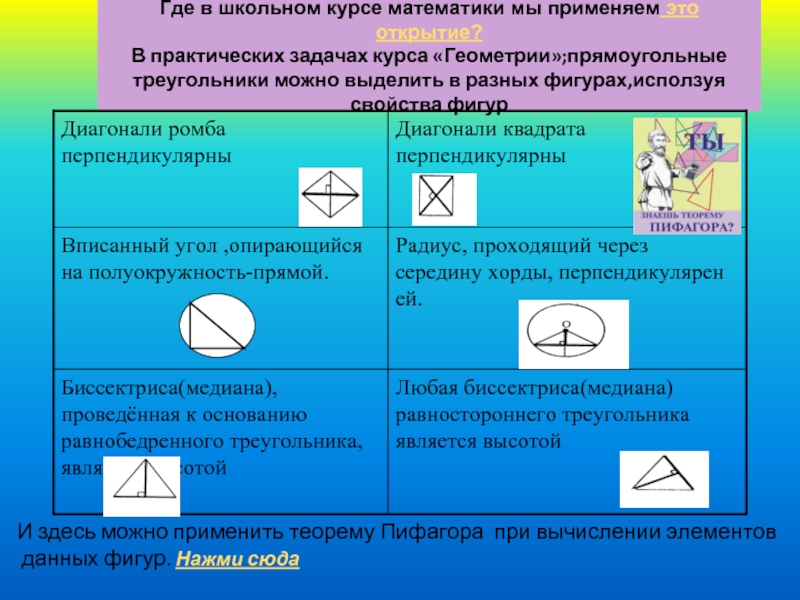
Где в школьном курсе математики мы применяем это открытие?
Когда впервые заговорили об этом открытии?

На самосском острове Я посетил множество стран и учился у

многих мыслителей того времени.

.

мифов, с моим именем связано многое в математике, и в

первую очередь, конечно, теорема носящая моё имя, которая занимает важнейшее место в школьном курсе геометрии.

Нажми сюда

Пифагор первый дал полноценное доказательство теоремы, носящей его имя.

К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают,
а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа.
В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают,
что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге.
Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал"

Нажми сюда

Формулировки теоремы Пифагора различны. Общепринятой считается следующая:
     
Во времена Пифагора формулировка

теоремы звучала так:

и называлось:
Сейчас известно около 150 различных доказательств этой теоремы

(геометрических, алгебраических, механических и т.д.)

а сама теорема –

«Dons asinorum»-
«ослиный мост»

или

“elefuga” -
«бегство убогих»

«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»

практических задачах курса «Геометрии»;прямоугольные треугольники можно выделить в разных фигурах,исползуя

свойства фигур

И здесь можно применить теорему Пифагора при вычислении элементов
данных фигур. Нажми сюда

теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких

доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса». Самостоятельное «открытие» доказательства теоремы Пифагора будет полезно и современным школьникам.