Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Классическое определение вероятности"
Содержание
- 1. "Классическое определение вероятности"
- 2. Ответьте на вопросы, выберите номер правильного ответа, запишите эти номера в таблицу.
- 3. 1. Событие «Из 25 студентов группы
- 4. 2. Назовите случайное событие _____. слово
- 5. 3. Достоверным является событие __. два попадания
- 6. 4. Среди пар событий, найдите несовместные _____.
- 7. 5. Охарактеризуйте случайное событие: новая электролампа не загорится. Это событие ___. менее вероятноеравновероятноеболее вероятное
- 8. 6. В колоде карт лежат четыре туза
- 9. 7. При бросании кубика выпало не больше
- 10. 8. Два стрелка делают по одному выстрелу
- 11. Ответы:
- 12. А. Н. Колмогоров (1903 – 1987)
- 13. Пьер-Симон Лаплас (1749-1827)
- 14. Классическое определение вероятности
- 15. Вероятностью P наступления случайного
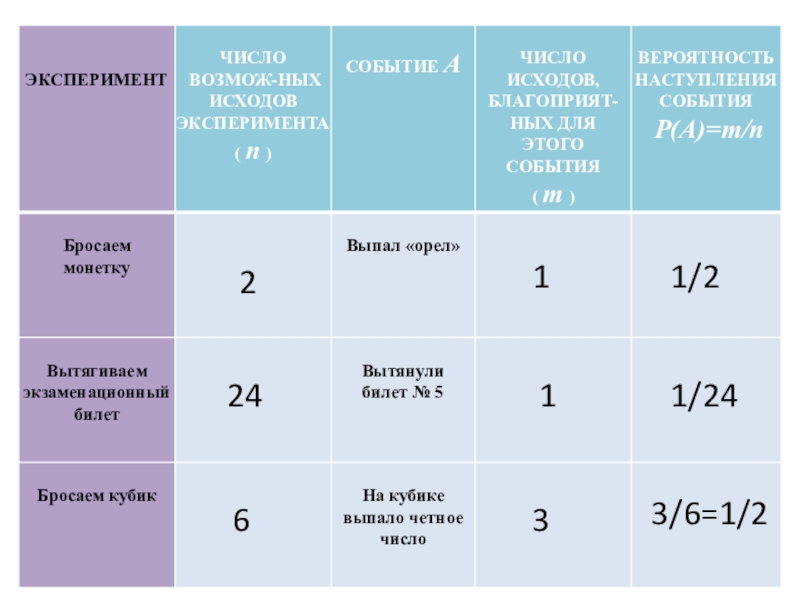
- 16. 211/22411/24633/6=1/2
- 17. Опишите все возможные исходы опыта, придумайте
- 18. Пример 2. При игре в нарды бросают
- 19. P(A)=6/36=1/6Решение:112233445566
- 20. Пример 3. Из карточек составили слово «статистика».
- 21. Решение: Всего 10 букв.Буква «с» встречается 2
- 22. Пример 4. В классе 20 студентов. Из
- 23. Решение: Число всех возможных исходов
- 24. Свойства вероятностиВероятность достоверного события равна 1. P(U)=1
- 25. Домашнее задание: 1. Найти вероятность того, что
- 26. 4. В клетки таблицы 2х2 ставят крестики
- 27. Скачать презентанцию
Ответьте на вопросы, выберите номер правильного ответа, запишите эти номера в таблицу.
Слайды и текст этой презентации
Слайд 3 1. Событие «Из 25 студентов группы двое справляют
день рождения 30 февраля» является ____.
достоверное
невозможное
случайное
Слайд 42. Назовите случайное событие _____.
слово начинается с буквы «ъ»
студенту второго курса 10 лет
бросили две игральные кости: сумма
выпавших на них очков равна 8Слайд 53. Достоверным является событие __.
два попадания при трех выстрелах
наугад выбранное
число, составленное из цифр 1,2,3 без повторений, меньше 400
подкинули монету,
и онаупала на «орла»
Слайд 64. Среди пар событий, найдите несовместные _____.
В сыгранной Катей и
Славой партии шахмат, Катя проиграла и Слава проиграл
Наступило лето; на
небе ни облачкаПри бросании кубика «выпало четное число», «выпало 2 очка»
Слайд 75. Охарактеризуйте случайное событие: новая электролампа не загорится. Это событие
___.
менее вероятное
равновероятное
более вероятное
Слайд 86. В колоде карт лежат четыре туза и четыре короля
разных мастей. Достают карту наугад. Противоположными являются события _____.
достанут трефового
тузадостанут туза любой масти
достанут любую карту, кроме трефового туза.
Слайд 97. При бросании кубика выпало не больше 5 очков. Количество
благоприятных исходов равно _____.
1
5
6
Слайд 108. Два стрелка делают по одному выстрелу в мишень. Количество
исходов двух совместных выстрелов равно _____.
2
3
4
Слайд 15 Вероятностью P наступления случайного события называется отношение
m/n , где n - число всех равновозможных
исходов эксперимента, а m - число всех благоприятных исходов:P(A)=m/n (1)
Слайд 17 Опишите все возможные исходы опыта, придумайте для них названия,
попробуйте их перечислить и убедитесь, что их конечное число.
Обоснуйте
равновозможность перечисленных исходов (здесь можно опираться на симметрию объекта, участвующего в опыте; использовать прямые указания в тексте задачи: «случайно», «наугад», «не глядя» и т.д.)Подсчитайте общее число исходов n .
Опишите благоприятные для события A исходы.
Подсчитайте число благоприятных для события A исходов m .
Вычислите вероятность по формуле P(A)=m/n .
Проверьте, согласуется ли полученная вероятность со «здравым смыслом».
Слайд 18Пример 2. При игре в нарды бросают 2 игральных кубика.
Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?
Слайд 20Пример 3. Из карточек составили слово «статистика». Какую карточку с
буквой вероятнее всего вытащить? Какие события равновероятные?
Слайд 21Решение:
Всего 10 букв.
Буква «с» встречается 2 раза – P(с) =
2/10 = 1/5;
буква «т» встречается 3 раза – P(т) =
3/10;буква «а» встречается 2 раза – P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза – P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз – P(к) = 1/10.
Слайд 22Пример 4. В классе 20 студентов. Из них 12 юношей,
остальные девушки. Известно, что к доске должны быть вызваны два
студента. Какова вероятность, что это девушки?Слайд 23Решение:
Число всех возможных исходов равно количеству способов,
которыми можно выбрать двух студентов из 30, т.е. n =
C230 = 435.Число благоприятных исходов равно m = C218 = 153.
Тогда P(A) = m/n = 51/145 .
А теперь сформулируем свойства вероятности.
- Чему равна вероятность достоверного (невозможного) события?
- Может ли быть, что вероятность
события равна 2, -1?
Слайд 24Свойства вероятности
Вероятность достоверного события равна 1. P(U)=1 (2)
Вероятность
невозможного события равна 0. P(V)=0 (3)
Вероятность события
A не меньше нуля,и не больше единицы.
0 ≤ P(A) ≤ 1 (4)
Слайд 25Домашнее задание:
1. Найти вероятность того, что при двукратном бросании кубика
произведение очков
а) кратно 5,
б) кратно 6.2. Из колоды в 36 карт случайным образом вытаскивают 3 карты. Найти вероятность того, что
а) нет пиковой дамы,
б) есть пиковая дама.
3. Случайно выбрали двузначное число.
Найдите вероятность того, что оно
а) оканчивается 0; б) состоит из одинаковых цифр; в) больше 27 и меньше 46; г) не является квадратом числа.
Слайд 264. В клетки таблицы 2х2 ставят крестики и нолики. Найдите
вероятность того, что
а) будет поставлен ровно один крестик,
б) будут поставлены ровно 2 нолика,в) в левой нижней клетке будет стоять крестик.
5. Эта задача – одна из первых по теории вероятностей – была предложена Галилею одним игроком в кости (Галилей дал правильное решение). Три кости подбрасываются одновременно. Что более вероятно – появление на трёх костях суммы 10 или 9?