Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классификация и свойства правильных многогранников
Содержание
- 1. Классификация и свойства правильных многогранников
- 2. Свойства многогранников Многогранники представляют собой
- 3. Исследуем возможность существования правильных многогранников. При этом
- 4. б) Пусть грани правильного многогранника – квадраты.
- 5. Доказал это соотношение один из величайших математиков
- 6. Теорема Эйлера. Пусть В - число вершин
- 7. ГЕКСАЭДР(КУБ)Куб составлен из шести квадратов. Каждая его
- 8. ДОДЕКАЭДРДодекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая
- 9. ТЕТРАЭДРТетраэдр составлен из четырех равносторонних треугольников. Каждая
- 10. ОКТАЭДРОктаэдр составлен из восьми равносторонних треугольников. Каждая
- 11. ИКОСАЭДРИкосаэдр составлен из двадцати равносторонних треугольников. Каждая
- 12. Слайд 12
- 13. Скачать презентанцию
Свойства многогранников Многогранники представляют собой простейшие тела в пространстве. Многогранные формы мы видим ежедневно: спичичный коробок, книга, комната, многоэтажный дом, граненый карандаш, гайка. С чисто геометрической точки зрения многогранник
Слайды и текст этой презентации
Слайд 1Классификация и свойства правильных многогранников
Теорема Эйлера
Автор работы :Кононов Саша 10в
Зинченко Вадим 10б
Слайд 2Свойства многогранников
Многогранники представляют собой простейшие тела в
пространстве. Многогранные формы мы видим ежедневно: спичичный коробок, книга, комната,
многоэтажный дом, граненый карандаш, гайка. С чисто геометрической точки зрения многогранник - это часть пространства, ограниченная плоскими многоугольниками - гранями. Грани образуют так называемую многогранную поверхность. На многогранную поверхность обычно накладывают следующие ограничения:1) каждое ребро должно являться общей стороной двух, и только двух, граней, называемых смежными;2) каждые две грани можно соединить цепочкой последовательно смежных граней;
3) для каждой вершины углы прилежащих к этой вершине граней должны ограничивать некоторый многогранный угол.
Многогранник называют выпуклым, если он лежит по одну сторону от плоскости любой из его граней. Это условие эквивалентно каждому из двух других: 1) отрезок с концами в любых двух точках многогранника целиком лежит в многограннике, 2) многогранник можно представить как пересечение нескольких полупространств.
Самые простые многогранники - четырехвершинники или четырехгранники - всегда ограничены четырьмя треугольными гранями. Но уже пятигранники могут быть совершенно разных типов. Как и многоугольники, многогранники характеризуются также по степени их симметричности. Среди пирамид выделяют правильные: в основании у них лежит правильный многоугольник, а высота-перпендикуляр, проведенный из вершины к плоскости основания, - попадает в центр основания пирамиды.
Слайд 3Исследуем возможность существования правильных многогранников. При этом будем опираться на
свойство плоских углов многогранного угла.
Теорема: Сумма плоских углов выпуклого многогранника
угла меньше 4d (3600).а) Пусть грани правильного многогранника – правильные треугольники. L = 600.
Если при вершине многогранного угла n плоских углов, то
600 n < 3600 ,
n < 6,
n = 3, 4, 5, т.е. существует 3 вида правильных многогранников с треугольными гранями. Это тетраэдр, октаэдр, икосаэдр.
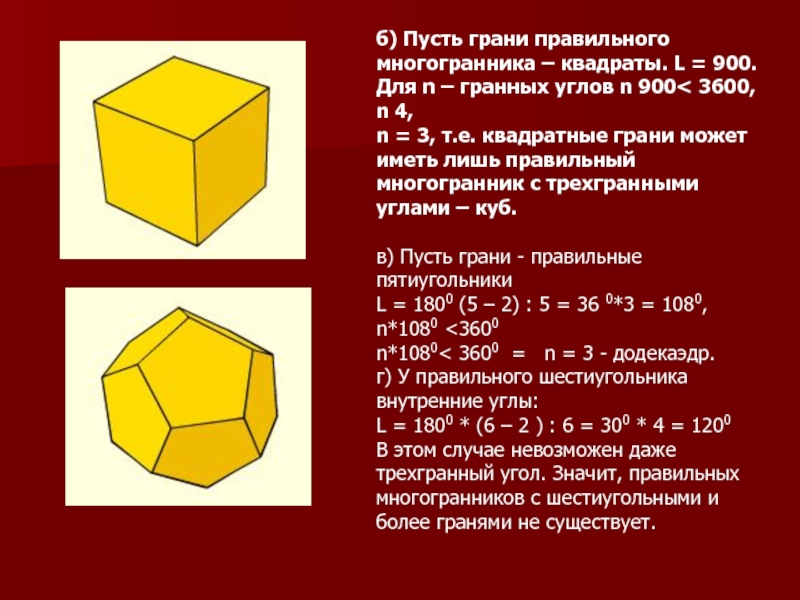
Слайд 4б) Пусть грани правильного многогранника – квадраты. L = 900.
Для
n – гранных углов n 900< 3600,
n 4,
n =
3, т.е. квадратные грани может иметь лишь правильный многогранник с трехгранными углами – куб.в) Пусть грани - правильные пятиугольники
L = 1800 (5 – 2) : 5 = 36 0*3 = 1080, n*1080 <3600
n*1080< 3600 = n = 3 - додекаэдр.
г) У правильного шестиугольника внутренние углы:
L = 1800 * (6 – 2 ) : 6 = 300 * 4 = 1200
В этом случае невозможен даже трехгранный угол. Значит, правильных многогранников с шестиугольными и более гранями не существует.
Слайд 5Доказал это соотношение один из величайших математиков Леонард Эйлер (1707
– 1783 гг.), поэтому формула названа его именем. Этот гениальный
ученый, родившийся в Швейцарии, почти всю жизнь прожил в России. Современная теория многогранников берет свое начало с его работ,Все эти примеры являются выводом теоремы Эйлера
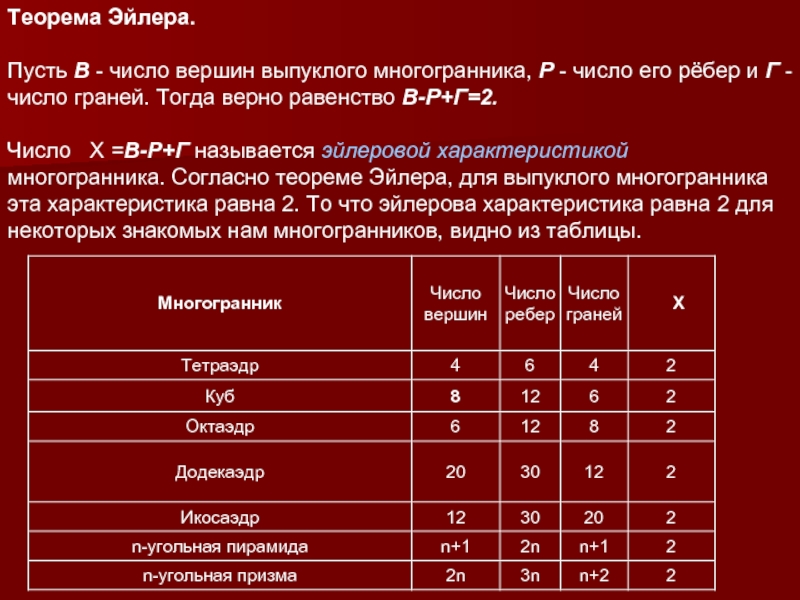
Слайд 6Теорема Эйлера.
Пусть В - число вершин выпуклого многогранника, Р
- число его рёбер и Г - число граней. Тогда
верно равенство В-Р+Г=2.Число X =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы.
Слайд 7ГЕКСАЭДР(КУБ)
Куб составлен из шести квадратов. Каждая его вершина является вершиной
трех квадратов. Сумма плоских углов при каждой вершине равна 270
градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.Слайд 8ДОДЕКАЭДР
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является
вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна
324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 реберСлайд 9ТЕТРАЭДР
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является
вершиной трех треугольников. Сумма плоских углов каждой при вершине равна
180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.Слайд 10ОКТАЭДР
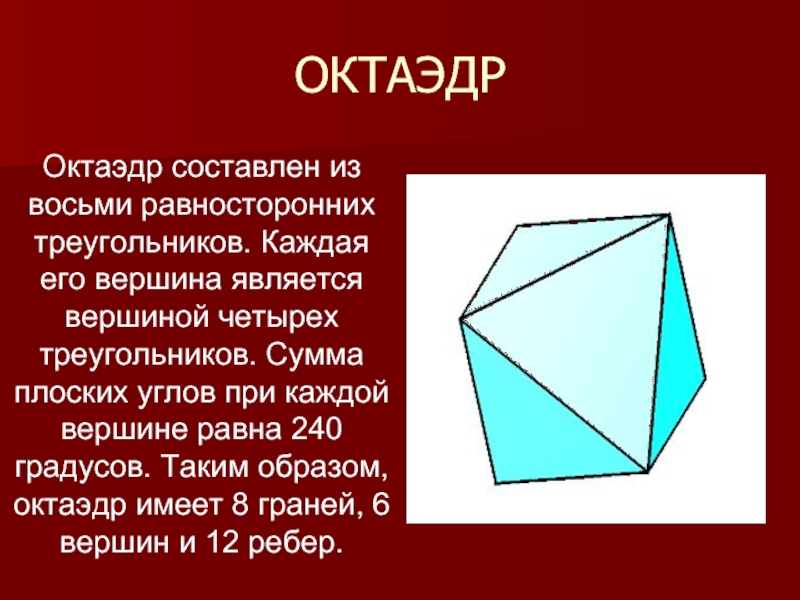
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является
вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна
240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.Слайд 11ИКОСАЭДР
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является
вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна
300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Теги