Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множество. Элемент множества
Содержание
- 1. Множество. Элемент множества
- 2. Слайд 2
- 3. Множество:множество четных чисел;множество двузначных чисел;множество правильных дробей
- 4. Объекты или предметы, составляющие множество, называют элементами множества. Например: число 89 – элемент множества двузначных чисел.
- 5. Слайд 5
- 6. Множества бывают конечные и бесконечные. Например: множество двузначных
- 7. Слайд 7
- 8. Пустое множество
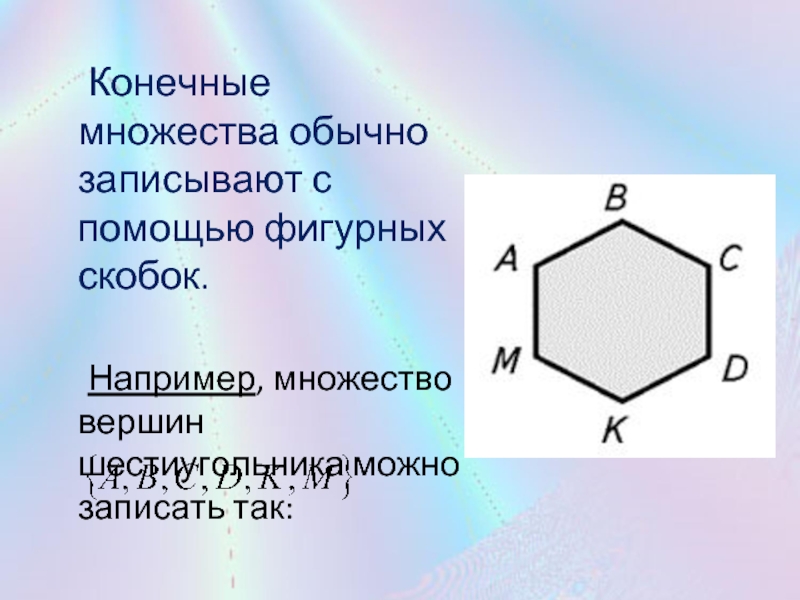
- 9. Конечные множества обычно записывают с помощью фигурных скобок. Например, множество вершин шестиугольника можно записать так:
- 10. Множества принято обозначать большими буквами латинского алфавита. Например, можно записать так
- 11. Для основных числовых множеств введены специальные обозначения:
- 12. В тех случаях, когда задание множества перечислением
- 13. множество всех натуральных чисел от 1 до
- 14. Скачать презентанцию
Множество:множество четных чисел;множество двузначных чисел;множество правильных дробей со знаменателем 5;множество диагоналей многоугольника;множество точек координатной плоскости;множество прямых, проходящих через данную точку.
Слайды и текст этой презентации
Слайд 3Множество:
множество четных чисел;
множество двузначных чисел;
множество правильных дробей со знаменателем 5;
множество
диагоналей многоугольника;
Слайд 4 Объекты или предметы, составляющие множество, называют элементами множества.
Например: число 89
– элемент множества двузначных чисел.
Слайд 6 Множества бывают конечные и бесконечные.
Например: множество двузначных чисел – конечное
множество (оно содержит 90 элементов),
а множество четных чисел – бесконечное
множество.Слайд 9 Конечные множества обычно записывают с помощью фигурных скобок.
Например, множество вершин
шестиугольника можно записать так:
Слайд 10 Множества принято обозначать большими буквами латинского алфавита.
Например, можно записать так
Слайд 11 Для основных числовых множеств введены специальные обозначения: множество натуральных чисел
обозначают буквой N (от латинского слова natural – «естественный», множество
целых чисел – буквой Z (от немецкого слова zahl – «число», множество рациональных чисел – буквой Q (от латинского слова quotient – «отношение»).Слайд 12 В тех случаях, когда задание множества перечислением элементов невозможно (как
для бесконечного множества) или громоздко (как для конечного множества с
большим числом элементов), множество задают описанием, указав его характеристическое свойство, т.е. свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.Слайд 13множество всех натуральных чисел от 1 до 14 включительно;
множество всех
натуральных чисел, меньших 15;
множество значений х, где и
Тот
факт, что множество А состоит из элементов х, удовлетворяющих этим условиям, будем записывать так:
Теги