Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конус
Содержание
- 1. Конус
- 2. Конусом называется тело, ограниченное кругом (основание конуса),
- 3. Конус – тело вращенияКонус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.
- 4. Боковая поверхность конуса – круговой сектор, радиус
- 5. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:Боковая поверхность конуса
- 6. Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:Полная поверхность конуса
- 7. Задача 1. Высота конуса равна 12, а
- 8. Сечения конуса различными плоскостямиСекущая плоскость проходит через
- 9. Сечения конуса различными плоскостямиЕсли секущая плоскость перпендикулярна
- 10. Вписанная пирамидаПирамида называется вписанной в конус, если
- 11. Описанная пирамидаПирамида называется описанной около кону-са, если
- 12. Задача 2Вокруг конуса описана правильная четырехугольная пирамида.
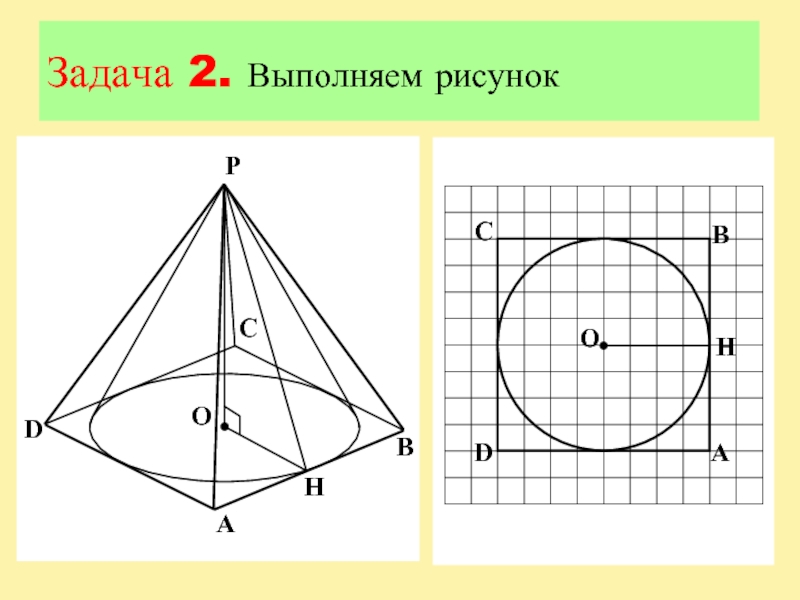
- 13. Задача 2. Выполняем рисунок
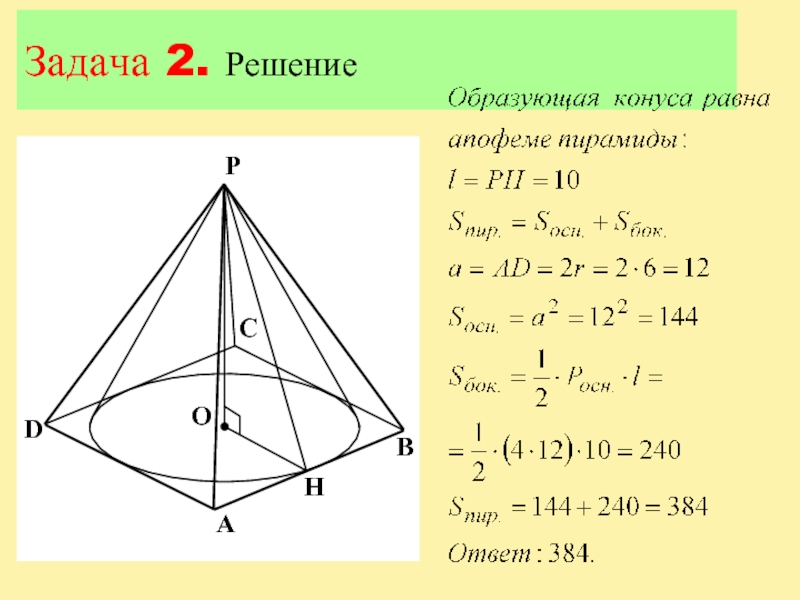
- 14. Задача 2. Решение
- 15. Задача 3В конус вписана правильная четырехугольная пирамида.
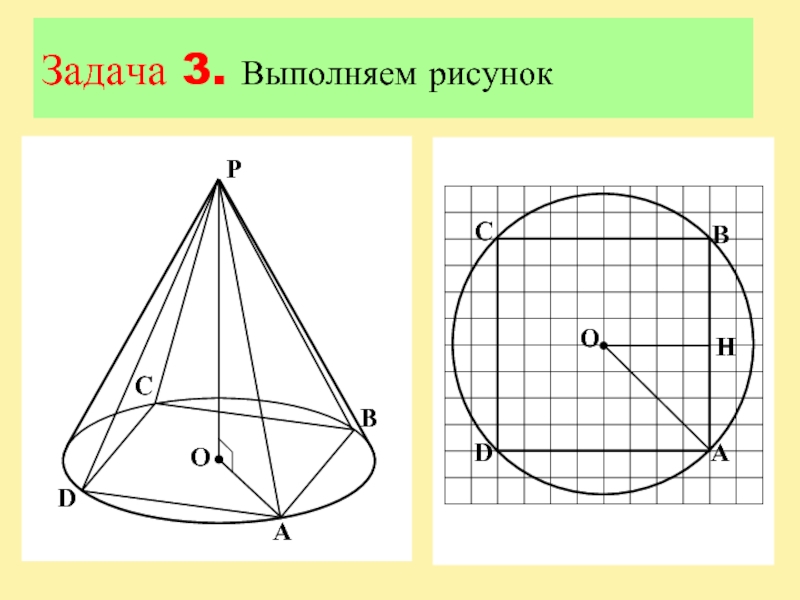
- 16. Задача 3. Выполняем рисунок
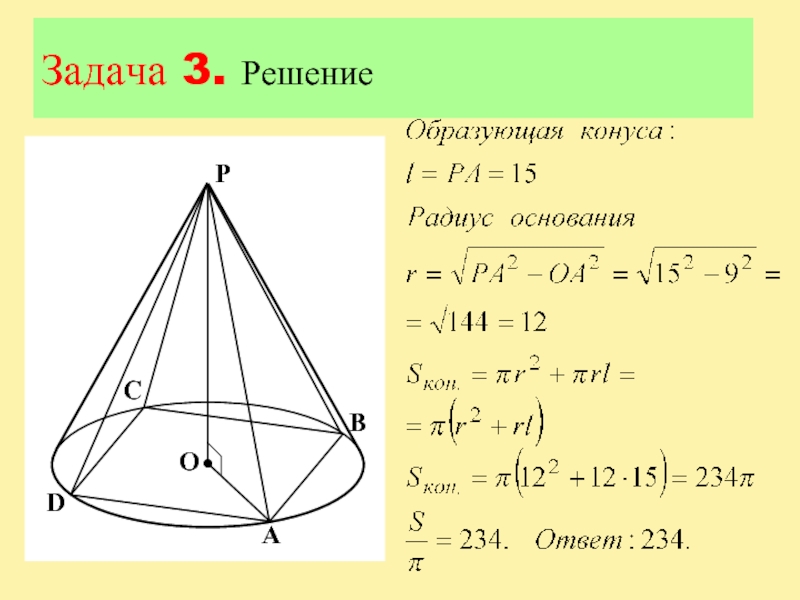
- 17. Задача 3. Решение
- 18. Аннотация:Данная презентация разработана для уроков геометрии в
- 19. Источники информации:1. Геометрия: учеб. для 10 –
- 20. Скачать презентанцию
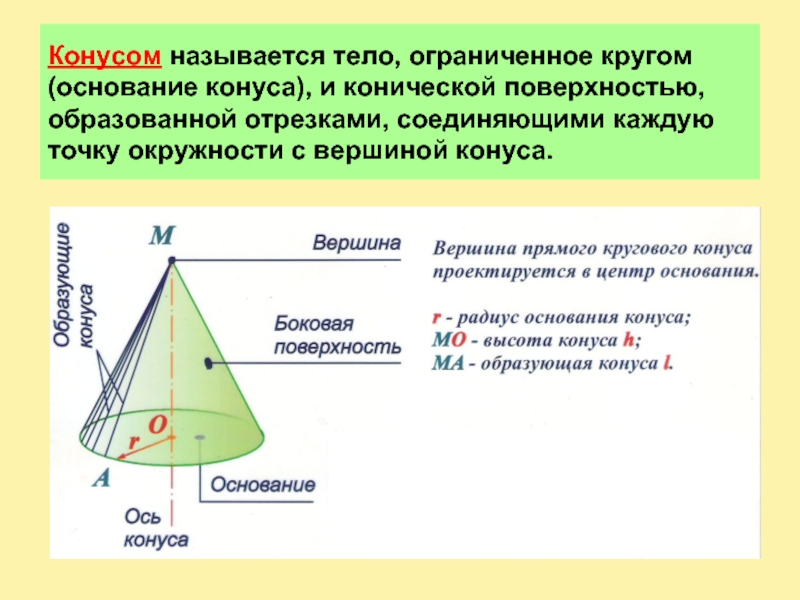
Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной отрезками, соединяющими каждую точку окружности с вершиной конуса.
Слайды и текст этой презентации
Слайд 1КОНУС
Стереометрия
11 класс
Выполнила:
учитель математики МБОУ СОШ №5
Приморско-Ахтарского района Краснодарского
края
Слайд 2Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью,
образованной отрезками, соединяющими каждую точку окружности с вершиной конуса.
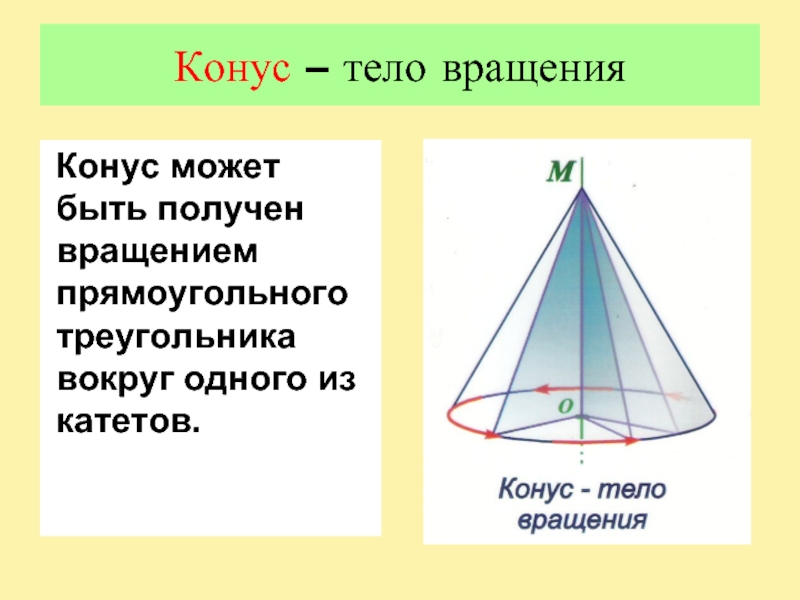
Слайд 3Конус – тело вращения
Конус может быть получен вращением прямоугольного треугольника
вокруг одного из катетов.
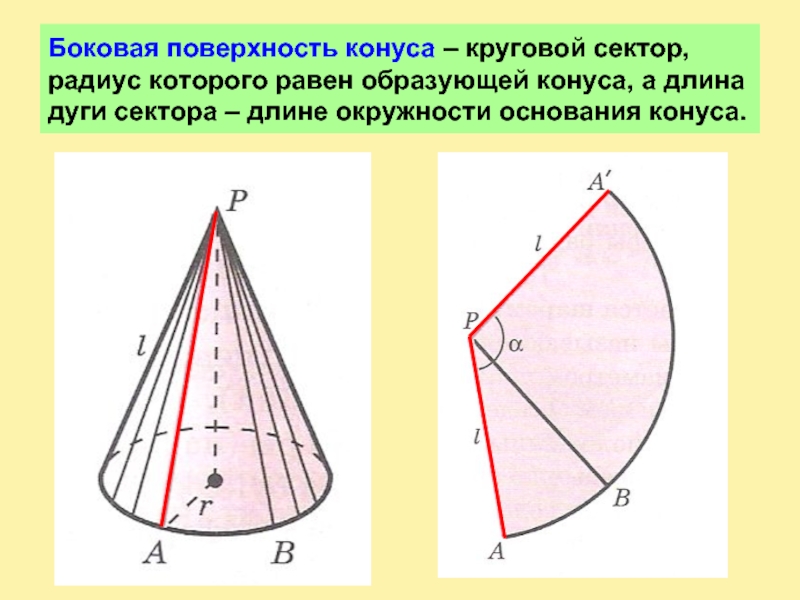
Слайд 4Боковая поверхность конуса – круговой сектор, радиус которого равен образующей
конуса, а длина дуги сектора – длине окружности основания конуса.
Слайд 5
Площадь боковой поверхности конуса равна произведению половины длины окружности основания
на образующую:
Боковая поверхность конуса
Слайд 6
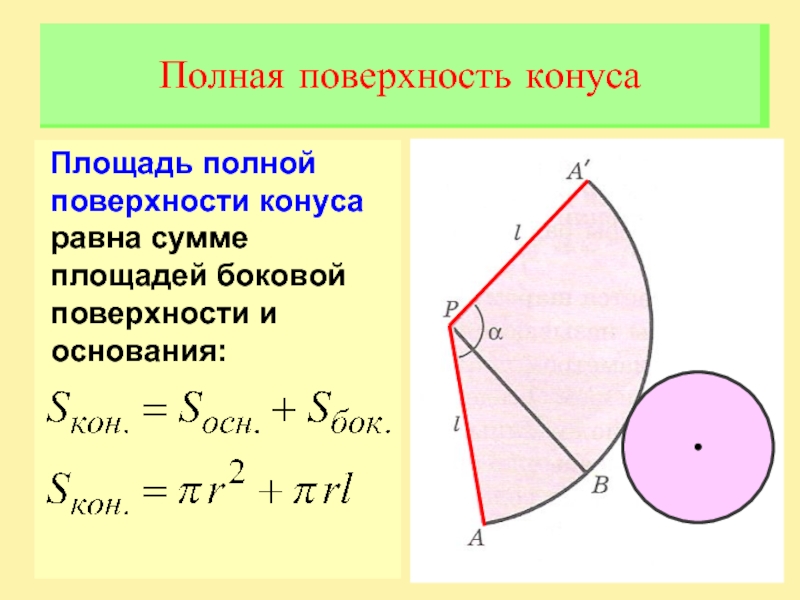
Площадь полной поверхности конуса равна сумме площадей боковой поверхности и
основания:
Полная поверхность конуса
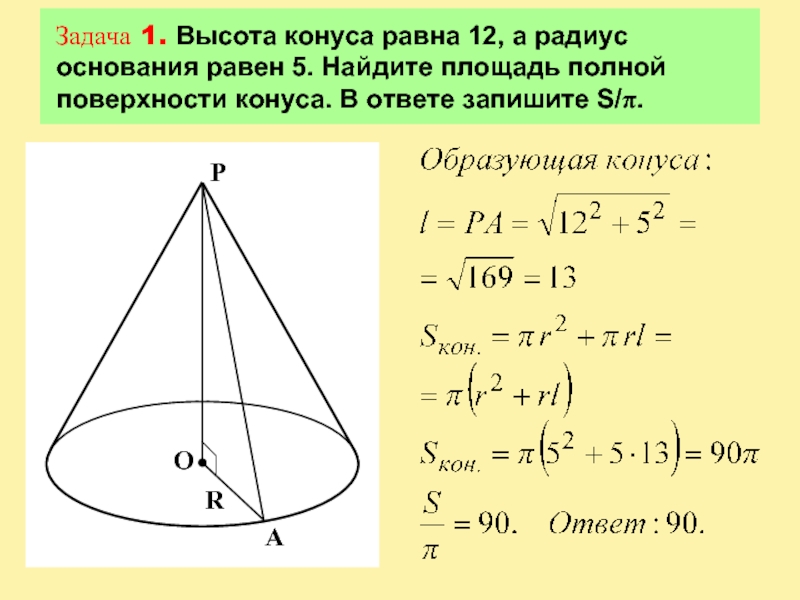
Слайд 7Задача 1. Высота конуса равна 12, а радиус основания равен
5. Найдите площадь полной поверхности конуса. В ответе запишите S/π.
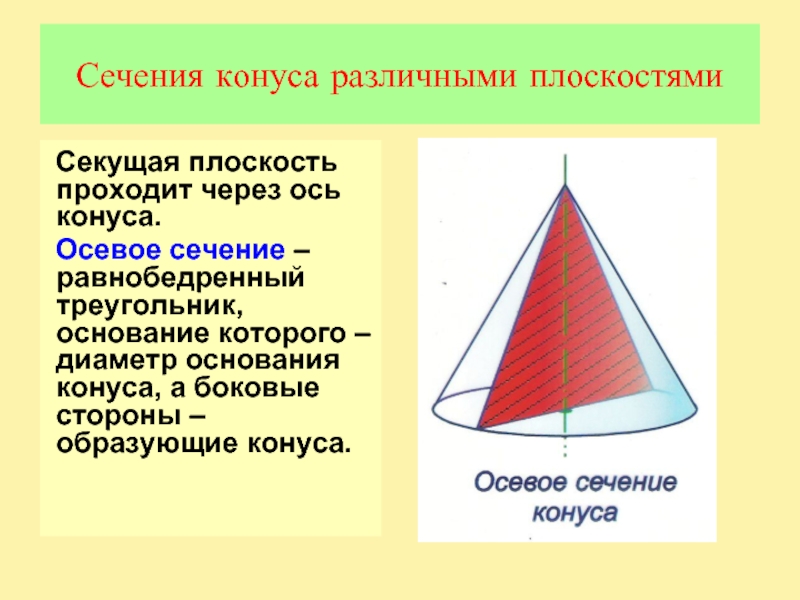
Слайд 8Сечения конуса различными плоскостями
Секущая плоскость проходит через ось конуса.
Осевое
сечение – равнобедренный треугольник, основание которого – диаметр основания конуса,
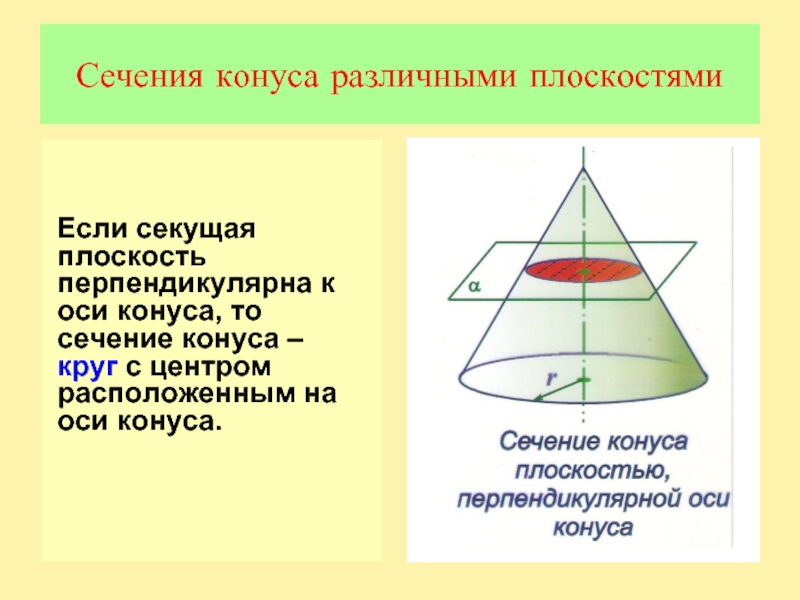
а боковые стороны – образующие конуса.Слайд 9Сечения конуса различными плоскостями
Если секущая плоскость перпендикулярна к оси конуса,
то сечение конуса – круг с центром расположенным на оси
конуса.
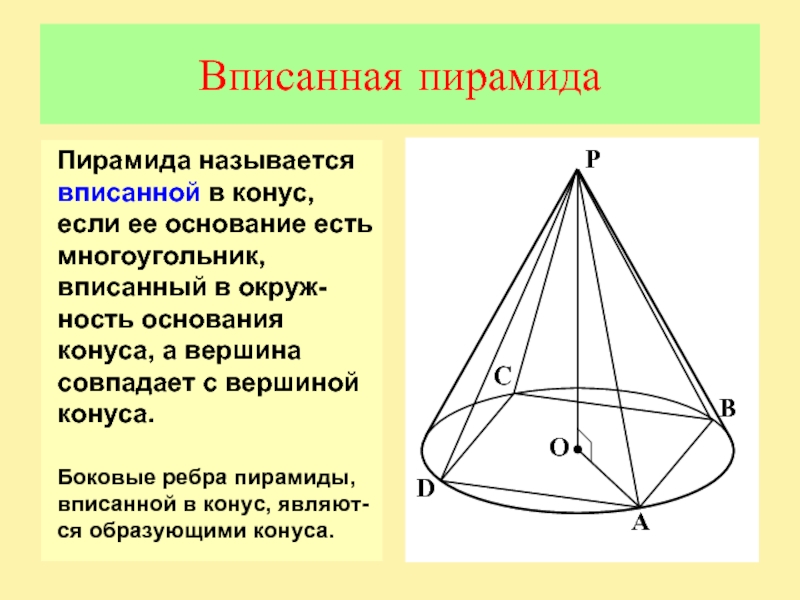
Слайд 10Вписанная пирамида
Пирамида называется вписанной в конус, если ее основание есть
многоугольник, вписанный в окруж-ность основания конуса, а вершина совпадает с
вершиной конуса.Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
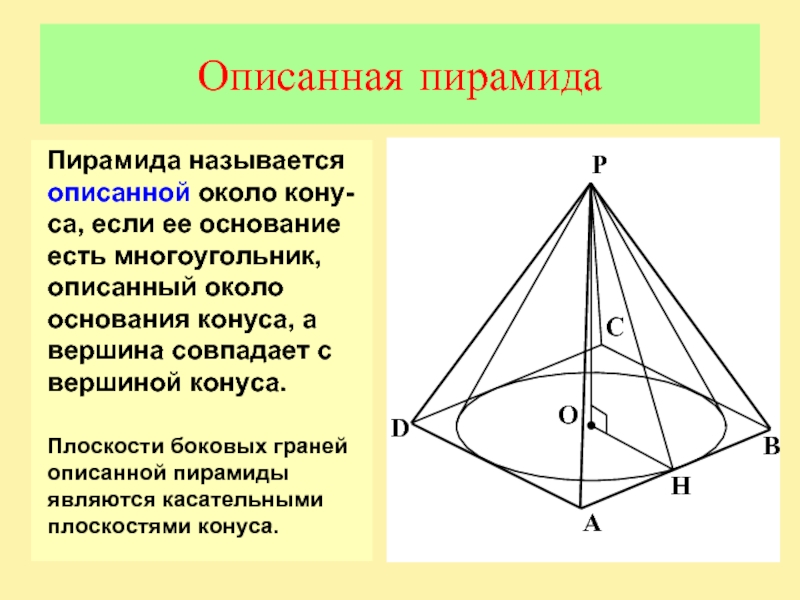
Слайд 11Описанная пирамида
Пирамида называется описанной около кону-са, если ее основание есть
многоугольник, описанный около основания конуса, а вершина совпадает с вершиной
конуса.Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
Слайд 12Задача 2
Вокруг конуса описана правильная четырехугольная пирамида. Найдите полную поверхность
пирамиды, если радиус основания конуса равен 6, а образующая конуса
равна 10.Слайд 15Задача 3
В конус вписана правильная четырехугольная пирамида. Найдите полную поверхность
конуса, если боковое ребро пирамиды равно 15, а ее высота
равна 9. В ответе запишите S/π.Слайд 18Аннотация:
Данная презентация разработана для уроков геометрии в 11 классе по
теме «Конус». В работе рассмотрены понятия конуса и его элементов,
«поверхность конуса», формула поверхности конуса, сечения конуса плоскостями. Рассмотрены так же понятия пирамиды, описанной около конуса, пирамиды, вписанной в конус. В презентации рассмотрены задачи из «Открытого банка заданий по математике», для закрепления рассмотренных понятий.Слайд 19Источники информации:
1. Геометрия: учеб. для 10 – 11 кл. общеобразовательных
учреждений / А.В. Погорелов. – М.: Просвещение, 2010.
2. Открытый банк
заданий по математике:http://mathege.ru
Теги
























![Сложение и вычитание вида []+4, []-4](/img/thumbs/605739bbda80b8f279b676f7db1e2062-800x.jpg)
