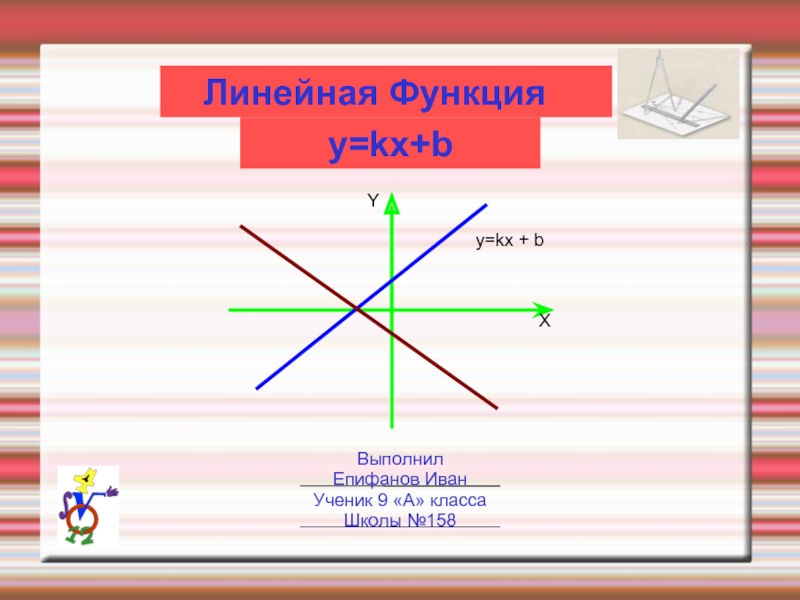
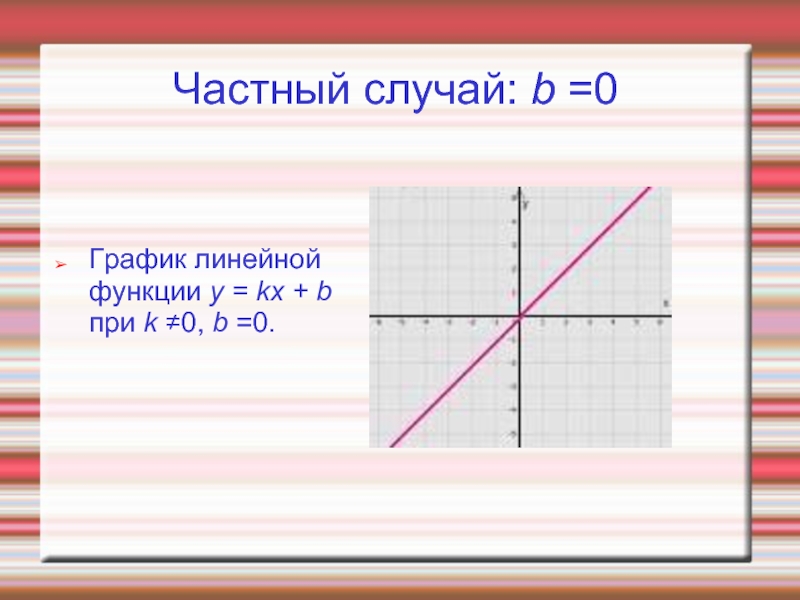
kx является прямая, проходящая через начало координат.
Коэффициент k называется
угловым коэффициентом этой прямой. Он равен тангенсу угла наклона этой прямой к оси X: k = tgα.
При положительных k этот угол острый, при отрицательных - тупой.