Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика
Содержание
- 1. Математическая логика
- 2. Правила пользования презентациейВыход в содержаниеВозврат к предыдущему слайдуПереход к следующему слайдуПодчёркнутое словоГиперссылка
- 3. СодержаниеПредисловиеЧто такое логика? - История
- 4. Предисловие
- 5. Предмет логики Логика (др.-греч. «λογική» — «искусство рассуждения») — наука, изучающая законы и формы мышления.
- 6. ИсторияКак самостоятельная наука логика оформилась в трудах
- 7. ВысказыванияВысказывание – утвердительное предложение, относительно которого можно
- 8. Алгебра высказыванийДизъюнкцияИмпликация ЭквиваленцияСтрогая дизъюнкцияКонъюнкцияДействия над высказываниямиОтрицание
- 9. Приоритет выполнения операцийАν(В ~С) ∧ А →
- 10. Законы математической логикиКоммутативность АВνАссоциативностьА ν В
- 11. Слайд 11
- 12. ОтрицаниеОтрицанием высказывания А называется такое высказывание, что
- 13. ДизъюнкцияДизъюнкцией высказываний А и В называется такое
- 14. импликацияИмпликацией высказываний А и В называется такое
- 15. конъюнкция Конъюнкцией высказываний А и В называется
- 16. эквиваленцияЭквиваленцией высказываний А и В называется такое
- 17. Строгая дизъюнкцияСтрогой дизъюнкцией высказываний А и В
- 18. Тогда, слушайте загадку!Да, капитан!Так точно, капитан!Я не
- 19. Разгадали? Давайте проверимПусть А≡{Капитан присутствует на судне},
- 20. ПредикатыУтверждение, зависящее от переменной, заданной на определенном
- 21. Множеством истинности предиката Р(х), заданного на множестве
- 22. Для предикатов характерны те же
- 23. Кванторы Одним из способов получения
- 24. квантор существования « ∃» Квантор существования
- 25. квантор всеобщности «∀» Квантор всеобщности
- 26. ЗаключениеТаким образом, мы познакомились с основными понятиями
- 27. Использованная литератураШабунин М.И. Математика. Алгебра. Начала анализа.http://ru.wikipedia.org
- 28. Работу выполнили Ученицы 11 А класса:Баженова НатальяЛуценко КсенияМасленникова ЛюдмилаСаяпина ЮлияПод руководством учителя математикиМигунова Фёдора Юрьевича
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Правила пользования презентацией
Выход в содержание
Возврат к предыдущему слайду
Переход к следующему
слайду
Слайд 3Содержание
Предисловие
Что такое логика?
- История изучения
- Высказывания
Алгебра логики
- Действия над высказываниями
- Приоритет выполнения операций- Законы алгебры логики
Примеры решения задач
Предикаты
Заключение
Слайд 4 Предисловие
В повседневной жизни
мы часто сталкиваемся с ситуациями, когда не знаем, как прийти
к выводу из предпосылок и получить истинное знание о предмете размышления. Логика служит одним из инструментов почти любой науки. Пример тому школьный курс математики.Слайд 5Предмет логики
Логика
(др.-греч. «λογική» — «искусство рассуждения») —
наука, изучающая законы и формы мышления.
Слайд 6История
Как самостоятельная наука логика оформилась в трудах греческого философа Аристотеля
(384-322 г.г до н.э.). Он систематизировал известные до него сведения,
и эта система стала впоследствии называться формальной или Аристотелевой логикой.Впервые в истории идеи о построении логики на математической основе были высказаны немецким математиком Г. Лейбницем (1646-1716) в конце XVII века. Он считал, что основные понятия логики должны быть обозначены символами, которые соединяются по особым правилам. Это позволит всякое рассуждение заменить вычислением.
Реализация идеи Лейбница принадлежит английскому учёному Д. Булю. Он создал алгебру, в которой буквами обозначены высказывания. Введение символических обозначений в логику имело для этой науки такое же решающее значение, как и введение буквенных обозначений для математики. Именно благодаря введению символов в логику была получена основа для создания новой науки – МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Слайд 7Высказывания
Высказывание – утвердительное предложение, относительно которого можно сказать истинно оно
или ложно.
Обычно высказывания обозначаются заглавными латинскими буквами, а само
предложение заключается в фигурные скобки.Понятие высказывания является исходным понятием математической логики.
Слайд 8Алгебра высказываний
Дизъюнкция
Импликация
Эквиваленция
Строгая дизъюнкция
Конъюнкция
Действия над высказываниями
Отрицание
Слайд 9Приоритет выполнения операций
Аν(В ~С) ∧ А → (ВνС)
1. Действия
в скобках
1
1
2
3
4
5
5. Импликация, эквиваленция, строгая дизъюнкция
4. Дизъюнкция
3. Конъюнкция
2. Отрицание
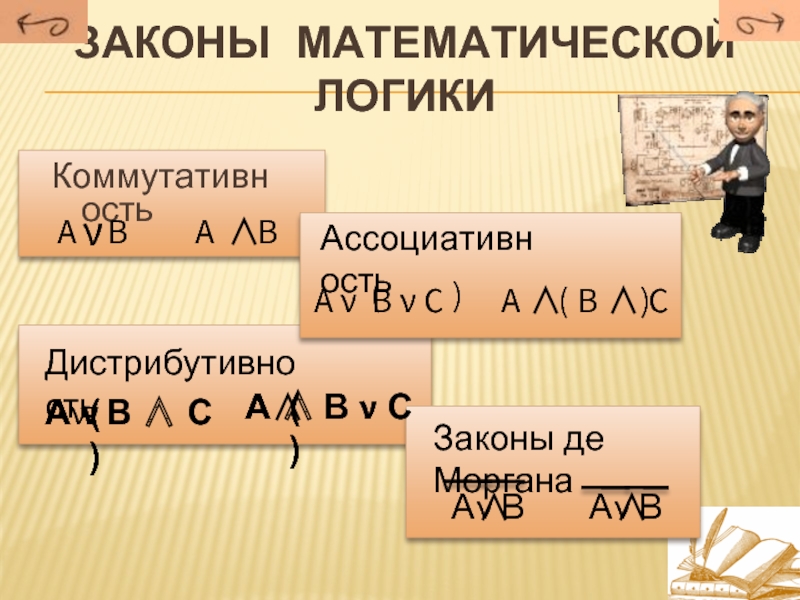
Слайд 10Законы математической логики
Коммутативность
А
В
ν
Ассоциативность
А ν В ν С
(
)
А ∧ В ∧ С
(
)Дистрибутивность
А
В
∧
А ν В ∧ С
( )
А
ν
( )
А ∧ В ν С
( )
А
∧
( )
Законы де Моргана
А
В
ν
∧
А
В
ν
∧
Слайд 11 Законы алгебры
логики
1. А = А
2. А ν А = А
3. А
∧ А = А4. А ν А = I
5. A ν (A ν A) = I
6. A ∧ (A ∧ A) = A
7. L = I
8. A ν L = A
9. A ∧ L = A
10. A ∧ A = L
I – тождественно-истинное высказывание
L – тождественно-ложное высказывание
Слайд 12Отрицание
Отрицанием высказывания А называется такое высказывание, что В ложно, когда
А истинно и В истинно, когда А ложно.
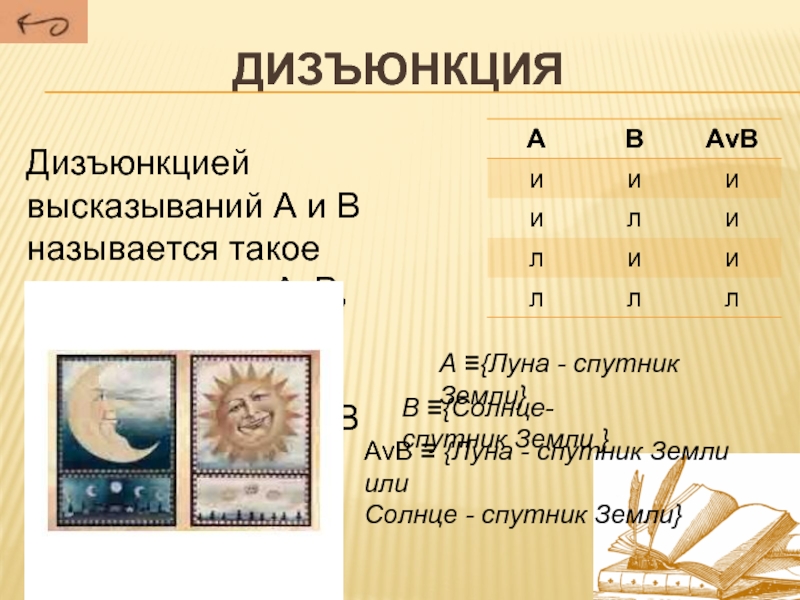
Слайд 13Дизъюнкция
Дизъюнкцией высказываний А и В называется такое высказывание АνВ, ложное
лишь в том случае, если оба высказывания А и В
ложные.АνВ ≡ {Луна - спутник Земли или
Солнце - спутник Земли}
A ≡{Луна - спутник Земли}
В ≡{Солнце- спутник Земли }
Слайд 14импликация
Импликацией высказываний А и В называется такое высказывание А→В, ложное
лишь в том случае, когда высказывание А – истинное и
В – ложное.A ≡ {Лето жаркое},
B ≡ {Зима будет холодной}
А→В ≡ {Eсли лето жаркое, то зима будет холодной.}
Слайд 15конъюнкция
Конъюнкцией высказываний А и В называется такое высказывание А∧В,
истинное лишь в том случае, если оба высказывания А и
В истинные.A ≡{Наталья учится в
11 а классе}
В ≡{Людмила учится в
11 а классе}
А∧В ≡ {Наталья и Людмила учатся вместе в 11 а классе}
Слайд 16эквиваленция
Эквиваленцией высказываний А и В называется такое высказывание А~В, истинное
когда А и В – оба истинные или оба ложные
высказывания.A ≡{Убийство раскрыто},
B ≡{Есть свидетели}
Для того чтобы раскрыть убийство необходимо и достаточно найти свидетелей.
Слайд 17Строгая дизъюнкция
Строгой дизъюнкцией высказываний А и В называют высказывание А⊕В,
истинное лишь в случаях, когда А – истинное и В
– ложное высказывание или А – ложное и В – истинное высказывание.А ≡ {Сейчас Ксюша в Москве}
В ≡ {Сейчас Ксюша в Лондоне}
А ⊕ В ≡ {Сейчас Ксюша в Москве или Лондоне}
Слайд 18Тогда, слушайте загадку!
Да, капитан!
Так точно, капитан!
Я не слышу!!
Согласно инструкции я
должен находиться на судне всегда, за исключением случаев, когда с
судна выгружают груз, если же груз не выгружают, то рулевой никогда не отсутствует, если не отсутствую и я. В каких случаях рулевой обязан присутствовать на судне?Вы готовы дети?
Слайд 19Разгадали? Давайте проверим
Пусть А≡{Капитан присутствует на судне},
В≡{С судна выгружают груз},
С≡{Рулевой присутствует на судне}, тогда (В → А) и (B→ (A→C)) – истинные высказывания.
Конъюнкция истинных высказываний истинна, т.е.
(B→A)∧(B→ (A→C))=(BvA)(B→(AvС))= (BvA)(Bv (AvС))= BvA(AvС)= BvLvAC= BvAC= B→AC.
Проанализировав полученное, выяснили, что рулевой присутствует на судне, если с судна не выгружают груз.
Ответ: рулевой присутствует на судне,
если с судна не выгружают груз.
Слайд 20Предикаты
Утверждение, зависящее от переменной, заданной на определенном множестве и обращающееся
в верное высказывание при конкретном значении переменной, называется неопределенным высказыванием
или предикатом.A(х) ≡ {d=x+34}
d
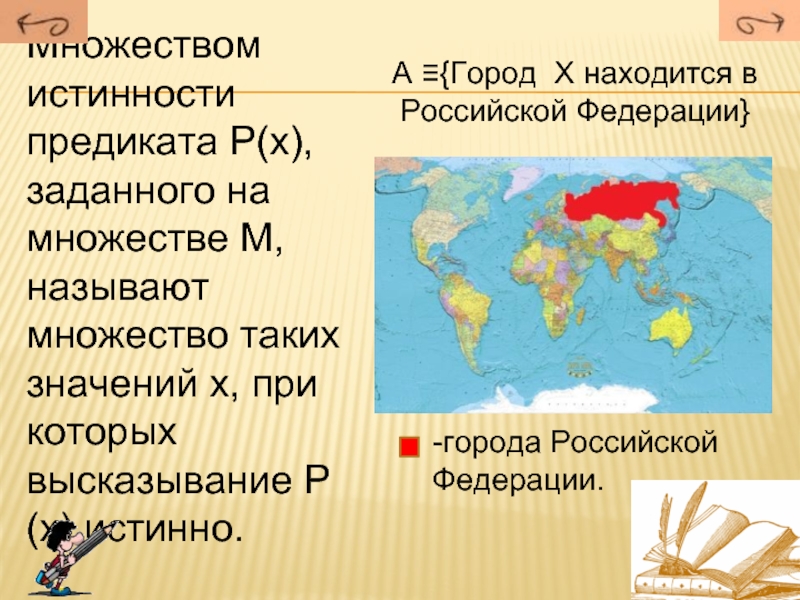
Слайд 21Множеством истинности предиката Р(х), заданного на множестве М, называют множество
таких значений х, при которых высказывание Р(х) истинно.
-города Российской
Федерации.A ≡{Город Х находится в Российской Федерации}
Слайд 22 Для предикатов характерны те же действия, что и
для высказываний, а именно:
Конъюнкция
Дизъюнкция
ИмпликацияЭквиваленция и др.
ПРЕДИКАТЫ
Слайд 23Кванторы
Одним из способов получения высказываний из предикатов
является навешивание кванторов. Для этого перед предикатом пишут кванторы –
слова, описывающие его множество истинности.А
Е
Квантор
существования
Квантор всеобщности
Слайд 24квантор существования « ∃»
Квантор существования — это символ,
обозначающий единственное существование и читается как «существует» или «для некоторого».
Из
предиката {Ученик X Лицея №1 сдал ЕГЭ по математике на 100 баллов } получаются высказывание:{Найдется такой ученик Лицея №1, который сдаст ЕГЭ по математике на 100 баллов}
Слайд 25квантор всеобщности «∀»
Квантор всеобщности — это символ,
обозначающий всеобщность и читается как «для любого» или «для всех».
Из предиката {Ученик X Лицея №1 сдал ЕГЭ по математике на 100 баллов } получаются высказывание:
{Все ученики Лицея №1 сдали ЕГЭ по математике на 100 баллов}