Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое описание случайных явлений (часть 1)
Содержание
- 1. Математическое описание случайных явлений (часть 1)
- 2. пункт 26. Элементарные события
- 3. Пункт 26 №1. Андрей и Борис решили
- 4. Вопрос : Сколько всего получилось элементарных событий?
- 5. РешениеРассмотрим все варианты событий какой вкус могут
- 6. Пункт 26 №3. Андрей, Борис и Владимир
- 7. Пункт 26 №3. Андрей, Борис и Владимир
- 8. Пункт 26 №4. В ящике четыре
- 9. Пункт 26 №4. В ящике четыре
- 10. Пункт 26 №4. В ящике четыре
- 11. Пункт 26 №5. Игральную кость подбрасывают
- 12. Подбросим монету два раза. Появление двух орлов
- 13. * Сколько элементарных событий при четырех бросаниях
- 14. Пункт 26 №7.Из закрепленного ружья стреляют по
- 15. А) При двух выстрелах, элементарных событий 10х10=100,
- 16. Пункт 26 №8. Спортивная команда «Математик» проводит
- 17. Пункт 26 №8. Спортивная команда «Математик» проводит
- 18. Пункт 26 №9. Красная Шапочка идет от
- 19. Пункт 26 №10. Красная Шапочка идет от
- 20. Пункт 26 №11. Игральную кость подбрасывают трижды.
- 21. Пункт 26 №12. Игральную кость подбрасывают трижды.
- 22. Пункт 26 №13. Игральную кость подбрасывают трижды.
- 23. Авторы решения задач №1 Носовкина Лиза№2 Александров
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическое описание случайных явлений
Часть 1
пункт 26.
Элементарные события
Решения задач
Проект
учащихся 8А класса
Афанасьева Светлана ВикторовнаСлайд 3Пункт 26 №1. Андрей и Борис решили купить мороженое и встали
в очередь. Сколькими способами они могут расположиться друг за другом?
Выпишите эти способы.Обозначим:
Андрея- буквой А, а Бориса- Б.
Друг за другом они могут расположиться только двумя способами
АБ или БА.
Слайд 4Вопрос :
Сколько всего получилось элементарных событий?
Условие
В киоске продаётся три сорта мороженого:
сливочное, шоколадное и клубничное. Андрей и Борис покупают по одной порции мороженого. Пункт 26 №2.
Слайд 5Решение
Рассмотрим все варианты событий какой вкус могут купить Борис и
Андрей.
Предположим, что Борис любит только шоколадное мороженное, тогда Андрей может
купить любое из трех видов. Если Борис любит клубничное, то Андрей снова может купить все три вкуса.
То же произойдет и с ванильным мороженным для Бориса.
Но если предположить, что Андрей любит только шоколадное мороженное, то тогда Борис может попробовать все три вкуса. Но это уже есть в нашей таблице.
Ответ: всего получилось 9 элементарных событий.
Слайд 6Пункт 26 №3. Андрей, Борис и Владимир решили купить мороженое и
встали в очередь за покупкой. Сколькими способами они могут расположиться
друг за другом? Выпишите все эти способы.Первый способ решения
Обозначим :
Андрея- буквой А,
Бориса- буквой Б,
Владимира- буквой В.
Следовательно, получается :
АБВ,АВБ, БАВ,БВА,ВАБ,ВБА.
Итого 6 способов.
Слайд 7Пункт 26 №3. Андрей, Борис и Владимир решили купить мороженое и
встали в очередь за покупкой. Сколькими способами они могут расположиться
друг за другом? Выпишите все эти способы.Второй способ решения
Первым может стоять
любой из 3 мальчиков,
следующим любой из 2, оставшийся мальчик будет последним( 1 вариант)
Получим 3!=1·2∙3=6
Итого 6 способов.
Слайд 8Пункт 26 №4. В ящике четыре детали: две исправные детали
а и Ь и две бракованные детали с и d.
Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.cdab не является элементарным событием,
так как все бракованные детали обнаружили
после второго извлечения.
а) Является ли сdаЬ элементарным событием в этом опыте?
б) Какими буквами может заканчиваться запись элементарного события?
запись элементарного события может заканчиваться буквами c или d.
Слайд 9Пункт 26 №4. В ящике четыре детали: две исправные детали
а и Ь и две бракованные детали с и d.
Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.
г) Сколько различных элементарных событий записывается тремя буквами?
в) Выпишите все элементарные события этого опыта.
Мы знаем, что запись элементарного события должна заканчиваться буквами c или d. Сначала запишем все события (элементарные и неэлементарные), а потом вычеркнем те, которые заканчиваются на буквы a и b.
Abcd badc cabd dabc
Abdc bacd cadb dacb
Adbс bdca cbad dbac
Adсb bdac cbda dbca
Acbd bcad cdab dcab
Acdb bcda cdba dcba
Посчитаем оставшиеся события : abcd, bdac, cabd, dabc, abdc, bacd, adbc, cbad, dbac, bdac, acbd,bcad, acdb.
Слайд 10Пункт 26 №4. В ящике четыре детали: две исправные детали
а и Ь и две бракованные детали с и d.
Из ящика наугад извлекают по одной детали, пока не обнаружат все бракованные. Элементарные события этого опыта будем записывать в виде последовательности букв. Например, аЬсd, саd и т. д.г) Сколько различных элементарных событий записывается тремя буквами?
Сначала составим все события:
Вычеркнем неэлементарные:
abc abd acd bcd
acb adb adc bdc
bac bad cad cbd
bca bda cda cdb
cab dba dac dbc
cba dab dca dcb
Остались события: acd, adc, cad, dac, bcd, bdc, cbd, dbc.
Всего: 8
Слайд 11Пункт 26 №5. Игральную кость подбрасывают дважды. Нарисуйте в тетради
таблицу элементарных событий этого эксперимента. Выделите в таблице элементарные события,
при которых в сумме выпало:г) четное число очков.
а) менее 4 очков
б) ровно 7 очков
в) ровно 11 очков
Слайд 12Подбросим монету два раза. Появление двух орлов записывается как ОО.
Это одно из элементарных событий этого опыта.
Подбросим монету три раза.
Выпишите все элементарные события этого опыта.Во сколько раз больше число элементарных событий при трёх бросаниях монеты, чем при двух бросаниях монеты?
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 1:
Элементарные события: ОО, РР,ОР, РО.
Опыт 2:
Элементарные события:
ООО,ООР, ОРО, ОРР, РРР, РОО, РОР, РРО.
Опыт 3:
В 2 раза.
Слайд 13* Сколько элементарных событий при четырех бросаниях монеты?
Опыт 4*:
16, т.к.
при подбрасывании выпадает 16
разных комбинаций:
2 варианта на первое подбрасывание (О
или Р)2 варианта на второе подбрасывание (О или Р)
2 варианта на третье подбрасывание (О или Р)
2 варианта на четвертое подбрасывание (О или Р) Всего: 2 ∙2 ∙2 ∙2 ∙2=16
* Сколько элементарных событий при десяти бросаниях монеты?
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 5*:
1024, т.к. при подбрасывании выпадает 1024 различных
комбинаций. Это можно узнать, возведя 2 в 10 степень.
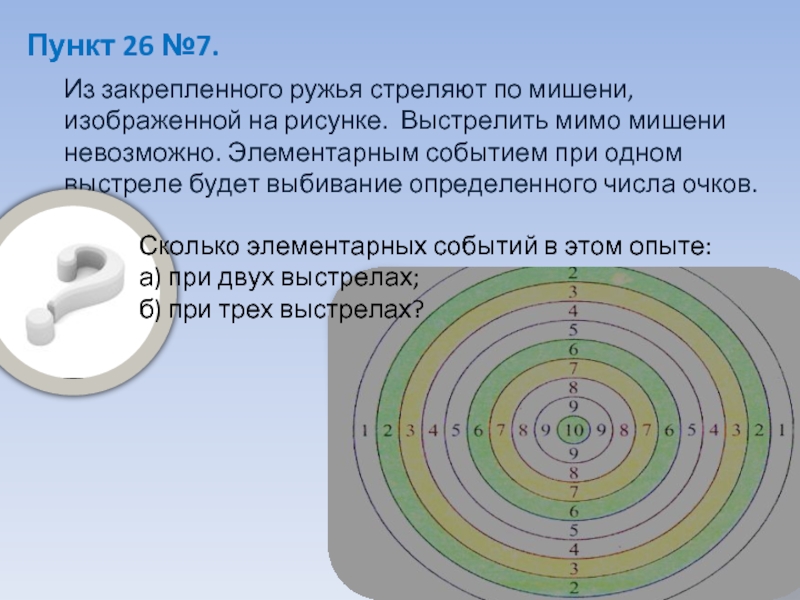
Слайд 14Пункт 26 №7.
Из закрепленного ружья стреляют по мишени, изображенной на
рисунке. Выстрелить мимо мишени невозможно. Элементарным событием при одном выстреле
будет выбивание определенного числа очков.Сколько элементарных событий в этом опыте:
а) при двух выстрелах;
б) при трех выстрелах?
Слайд 15А) При двух выстрелах, элементарных событий 10х10=100, к каждому из
десяти возможных элементарных событий при первом выстреле может присоединиться любое
из десяти событий при втором выстреле. Все эти 100 элементарных событий записаны в таблице.Б) При трёх выстрелах, элементарных событий 10х10х10=1000, к каждому из десяти возможных элементарных событий при первом выстреле может присоединиться любое из десяти событий при втором выстреле и может присоединиться любое из десяти событий при третьем выстреле.
а) При двух выстрелах 100 элементарных событий
б) При трёх выстрелах 1000 элементарных событий.
Слайд 16Пункт 26 №8. Спортивная команда «Математик» проводит товарищескую встречу по
волейболу с командой «Физик». Ничья невозможна. Встреча проводится до двух
побед одной из команд. Победу «Математика» обозначим буквой М, а победу «Физика»— буквой Ф. Одним из элементарных событий является ММ.а) Запишите все возможные элементарные события.
б) Запишите все элементарные события, при которых встречу выигрывает команда «Физик».
Элементарные события :
ММ,ФФ,МФМ, ФММ, ФМФ,МФФ
ФФ,ФМФ,МФФ
Две буквы Ф, одна из которых является последней
Слайд 17Пункт 26 №8. Спортивная команда «Математик» проводит товарищескую встречу по
волейболу с командой «Физик». Ничья невозможна. Встреча проводится до двух
побед одной из команд. Победу «Математика» обозначим буквой М, а победу «Физика»— буквой Ф. Одним из элементарных событий является ММ.в) Предположим, что во встрече победила команда «Математик». Какой буквой оканчивается запись соответствующих элементарных событий?
г) Какое наибольшее количество матчей может состояться?
Запись оканчивается буквой М
3 матча
Если после первых двух игр победитель не определился,
то победитель третьего матча станет победителем встречи
Слайд 18Пункт 26 №9. Красная Шапочка идет от домика мамы до
домика бабушки. Красная Шапочка может идти только по дорожкам слева
направо. Схема дорожек показана на рисунке. Каждая дорожка обозначена буквой. Например, один из возможных путей записывается как ах, другой — как bz. Перечислите все возможные пути Красной Шапочки в домик бабушки. Сколько получилось таких путей?
Слайд 19Пункт 26 №10. Красная Шапочка идет от домика мамы до
домика бабушки. Красная Шапочка может идти только по дорожкам слева
направо. Схема дорожек показана на рисунке. Каждая дорожка обозначена буквой. Сколько элементарных событий в этом опыте записывается одной, двумя, тремя буквами?1) Одной буквой может быть записано 2 элементарных события: d и w.
2) Двумя буквами может быть записано 2 элементарных события: ax и bx.
3) Тремя буквами может быть записано 4 элементарных события: auw, buw, avw, bvw
Слайд 20Пункт 26 №11. Игральную кость подбрасывают трижды. Сколько элементарных событий
в этом эксперименте?
У кости 6 граней, следовательно
количество элементарных
событий равно6·6·6=216
Слайд 21Пункт 26 №12. Игральную кость подбрасывают трижды. Найдите число элементарных
событий, при которых в сумме выпало: а) 2 очка; б)
З очка; в) 4 очка.а) 0, т.к это невозможное событие.
б)1, при выпадении 111
в)3, при выпадении 112,121,211
Слайд 22Пункт 26 №13. Игральную кость подбрасывают трижды. Найдите число элементарных
событий, при которых в сумме выпало более: а) 17 очков;
б) 16 очков; в) 15 очков.а) «выпало более17 очков»
элементарное событие: 6+6+6
Всего 1 элементарное событие.
б) «выпало более16 очков»
элементарные события: 5+6+6, 6+6+5, 6+5+6, 6+6+6.
Всего 4 элементарных события.
в) «выпало более15 очков».
элементарные события:
4+6+6, 6+6+4, 6+4+6,
5+5+6, 5+6+5, 6+5+5,
5+6+6, 6+5+6, 6+6+5,
6+6+6. Всего 10 элементарных событий.
Слайд 23Авторы решения задач
№1 Носовкина Лиза
№2 Александров Лев
№3 Низамова Наташа
№4 Соколова
Даша
№5 Зюбан Полина
№6 Жучкова Мария
№7 Синицын Дима
№8 Русин Илья
№9 Колягин
Влад№10 Носовкина Лиза
№11 Носовкина Лиза №12 Корякина Таня
№13 Корякина Таня
На фотографиях учащиеся нашего класса на уроке компьютерного эксперимента по теории вероятностей