Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Золотое сечение" в нашей жизни
Содержание
- 1. "Золотое сечение" в нашей жизни
- 2. Геометрия владеет двумя сокровищами: одно из них
- 3. Построим золотое сечениеАВАВСАВСВС=- АВ12АВСДАВСДЕ СД = ВСАЕ
- 4. Принято считать, что понятие о золотом делении
- 5. Внимание людей издавна привлекала совершенство формы пятиконечная
- 6. Слайд 6
- 7. Из книги Д. Брауна «Код да Винчи»…Мысленно
- 8. Слайд 8
- 9. Начиная с вирусов и растений, и заканчивая
- 10. Биение сердца –около 60 уд/мин.Давление крови наибольшей
- 11. Еще в древности основу скульптуры составляли теории
- 12. Измерения нескольких тысяч человеческих тел
- 13. Великий древнегреческий скульптор Фидий часто использовал “золотое
- 14. Рассмотрим размеры пирамиды Хеопса:Длина стороны основания- 500
- 15. Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари)
- 16. Долгое время считали, что зодчие Древней
- 17. Слайд 17
- 18. ЗОЛОТОЕ СЕЧЕНИЕМатематика в живописи
- 19. В особый вид изобразительного искусства Древней Греции
- 20. Переходя к примерам “золотого сечения” в живописи,
- 21. Слайд 21
- 22. Нет живописи более поэтичней,чем живопись Боттичелли Сандро,
- 23. Слайд 23
- 24. Рафаэль Санти не был ученым-математиком, но подобно
- 25. Золотое сечение в картине И. И. Шишкина"Сосновая
- 26. И.Е.Репин «А.С.Пушкин на акте в Лицее8 января
- 27. Н.Ге «А.С.Пушкин в селе Михайловском»Фигура А.С.Пушкина поставлена художником слева на линии золотого сечения
- 28. В.Суриков «Боярыня Морозова»Роли боярыни отведена средняя часть
- 29. Максимальная громкость звука , которая начинает вызывать
- 30. музыка есть арифметическое упражнение души,которая исчисляет
- 31. Алгебра музыкиВ композиции многих музыкальных произведений отмечается
- 32. Наибольшее количество музыкальных произведений, в которых имеется
- 33. ученый М.А.Марутаев подсчитал количество тактов в знаменитой
- 34. Поэзия А.С.Пушкина- образец наиболее выдающихся творений мировой
- 35. Примеры из поэзии бесчисленны. Особенно ими изобилует
- 36. Представляет несомненный интерес анализ романа "Евгений Онегин",
- 37. Слайд 37
- 38. Поверить алгеброй гармониюЗнаменитое стихотворение Лермонтова "Бородино" делится
- 39. Сенсационное открытие сделал петербургский поэт и переводчик
- 40. Золотое сечение в фотографииПринято считать, что
- 41. Т.е.расположение основных компонентов кадра в особых точках-зрительных
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Геометрия владеет двумя сокровищами: одно из них – это теорема
Пифагора, а другое- деление отрезка в крайнем и среднем отношении… Первое
можно сравнить с мерой золота; второе же больше напоминает драгоценный камень. Иоганн Кеплер Золотое сечение –это такое деление
целого на две неравные части, при
котором целое так относится к большей
части, как большая к меньшей.
Ф-такое обозначение принято в честь
древнегреческого скульптора Фидия
(V век до н.э.)
«Золотое сечение» - это иррациональное
число, оно приблизительно равно 1, 618.
Слайд 3
Построим золотое сечение
А
В
А
В
С
А
В
С
ВС=- АВ
1
2
А
В
С
Д
А
В
С
Д
Е
СД = ВС
АЕ = АД
Точка Е
делит отрезок АВ в соотношении ЗОЛОТОЙ ПРОПОРЦИИ
Просмотри, продумай показанный этап
Слайд 4Принято считать, что понятие о золотом делении ввел в научный
обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.).
Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.Пифагор
Античный циркуль золотого сечения
Слайд 5Внимание людей издавна привлекала совершенство формы пятиконечная звезда.
АD:АС
= АС:СD=АВ:ВС=Ф.
Пятиконечной звезде - около 3000 лет. Ее первые изображения
донесли до нас вавилонские глиняные таблички. Из древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком. Сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира. Чем же объясняется такая популярность? Тем, что совершенная форма этой фигуры радует глаз. Звездчатый пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции.
Одной из причин, по которой пифагорейцы избрали пентаграмму, или пятиконечную звезду, символом своего тайного ордена, является то обстоятельство, что любой отрезок в этой фигуре находится в золотом отношении к наименьшему соседнему отрезку.
Слайд 6
Итальянский
математик, монах Леонардо из Пизы, более известен под именем Леонардо
Фибоначчи (сын Боначчи).Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими ) цифрами.В 1202 году вышел в свет его труд «Книга об абаке» (счетной доске), в котором были собраны все известные в то время задачи.Одна из задач гласила: «Сколько пар кроликов в один год от одной пары родится?»
Размышляя на эту тему, Фибоначчи выстроил такой ряд чисел:
месяцы 0 1 2 3 4 5 6 7 8 910 ...
пары кроликов
0 1 1 2 3 5 8 13 21 …
Ряд чисел 0 1 1 2 3 5 8 13 21 34 55 89… стал известен как ряд Фибоначчи.
Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих: 2+3=5; 3+5=8; 5+8=13…,
а отношение смежных чисел ряда приближается отношению золотого сечения.Так 21:34 =0,617, а 89:55 =0,618
В дальнейшем мы увидим, что
числа Фибоначчи часто появляются в самых неожиданных местах, при этом неотступно сопровождая золотую пропорцию.
Числа Фибоначчи
Слайд 7Из книги Д. Брауна «Код да Винчи»
…Мысленно он перенесся в
Гарвард, увидел себя перед аудиторией. Вот он поворачивается к доске,
где мелом выведена тема «Символизм в искусстве». И пишет под ней свое любимое число 1, 618А затем оборачивается и ловит любопытные взгляды студентов.
– Кто скажет мне, что это за число?
Сидящий в последнем ряду длинноногий математик Стетнер поднимает руку.
– Это число PHI. – Произносит он его как «фи-и».
. . . число PHI получено из последовательности Фибоначчи, математической прогрессии, известной не только тем, что сумма двух соседних чисел в ней равна последующему числу, но и потому, что частное двух соседствующих чисел обладает уникальным свойством – приближенностью к числу 1, 618, то есть к числу PHI!
И далее Лэнгдон объясняет, что, несмотря на почти мистическое происхождение, число PHI сыграло по-своему уникальную роль. Роль кирпичика в фундаменте построения всего живого на земле. Все растения, животные и даже человеческие существа наделены физическими пропорциями, приблизительно равными корню от соотношения числа PHI к 1.
– Эта вездесущность PHI в природе указывает на связь всех живых существ. Раньше считали, что число PHI было предопределено Творцом вселенной. Ученые древности называли одну целую шестьсот восемнадцать тысячных «божественной пропорцией».
Слайд 9Начиная с вирусов и растений, и заканчивая организмом человека, всюду
выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое
сечение признано универсальным законом живых систем.Приглядимся к побегу цикория. От оси его стебля образовался отросток. Тут же расположился первый листок. Отросток делает выброс, выпускает листок, но уже короче первого, снова делает выброс, но уже меньшей силы и т.д.
Если первый выброс принять за 100 единиц, то второй равен 62, третий-38 и т. д. Длина лепестков тоже подчинена золотой пропорции.
У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции
У стрекозы отношение длины хвоста и корпуса равно отношению общей длины к длине хвоста.
Золотое сечение в биологии
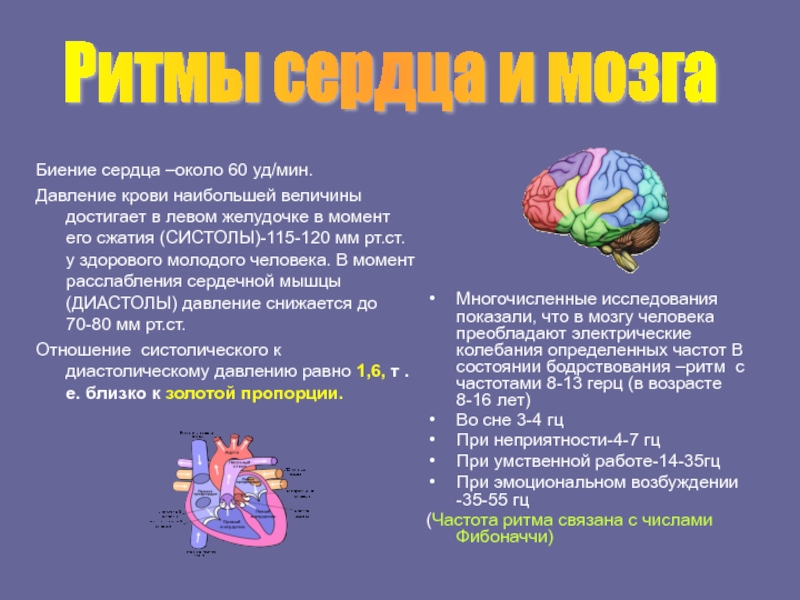
Слайд 10Биение сердца –около 60 уд/мин.
Давление крови наибольшей величины достигает в
левом желудочке в момент его сжатия (СИСТОЛЫ)-115-120 мм рт.ст. у
здорового молодого человека. В момент расслабления сердечной мышцы (ДИАСТОЛЫ) давление снижается до 70-80 мм рт.ст.Отношение систолического к диастолическому давлению равно 1,6, т . е. близко к золотой пропорции.
Многочисленные исследования показали, что в мозгу человека преобладают электрические колебания определенных частот В состоянии бодрствования –ритм с частотами 8-13 герц (в возрасте 8-16 лет)
Во сне 3-4 гц
При неприятности-4-7 гц
При умственной работе-14-35гц
При эмоциональном возбуждении -35-55 гц
(Частота ритма связана с числами Фибоначчи)
Ритмы сердца и мозга
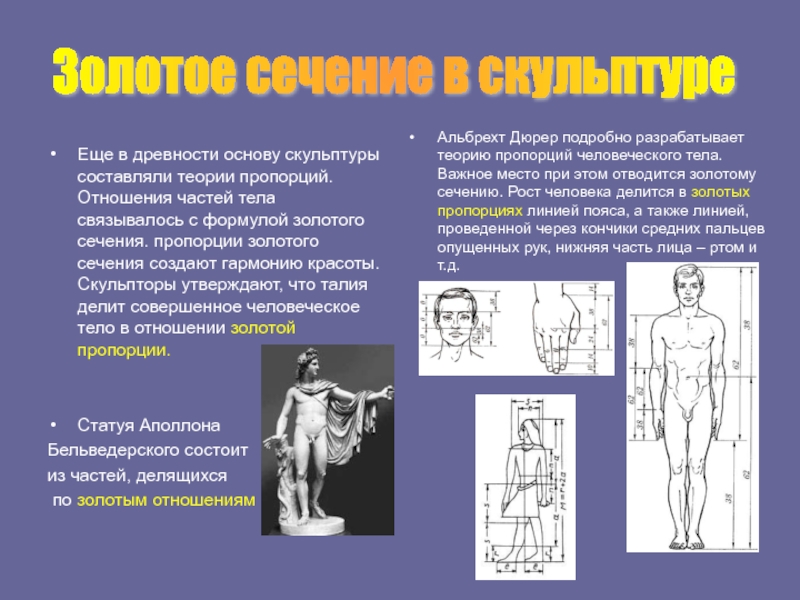
Слайд 11Еще в древности основу скульптуры составляли теории пропорций. Отношения частей
тела связывалось с формулой золотого сечения. пропорции золотого сечения создают
гармонию красоты. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении золотой пропорции.Статуя Аполлона
Бельведерского состоит
из частей, делящихся
по золотым отношениям
Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место при этом отводится золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д.
Золотое сечение в скульптуре
Слайд 12 Измерения нескольких тысяч человеческих тел позволило обнаружить
что для взрослых мужчин это отношение равно 13:8=1,625,
а
взрослых женщин оно составляет 8:5 = 1,6.Так что пропорции мужчин ближе к “золотому сечению”.
Слайд 13Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих
произведениях.
Самая знаменитая из них была статуя Зевса Олимпийского, которая
считалась одним из чудес света и статуя Афины Парфенос.Слайд 14
Рассмотрим размеры пирамиды Хеопса:
Длина стороны основания- 500 локтей
Высота пирамиды –
примерно 318 локтей
Апофема боковой грани – 404, 5 локтя
Длина боковых
ребер – 475, 5 локтяS основания пирамиды-250000кв.локтей
S бок.грани- 101125 кв.локтей
Отношение поверхности граней к площади основания равно 1.6…, т.е.золотой пропорции
Зодчие Древней Греции оставили нам великолепные памятники архитектуры. И среди них первое место по праву принадлежит Парфенону.
Отношение длины здания Парфенона к его высоте равно Ф
КВ:АВ=СВ:АС=АВ:ВС= Ф
Золотая пропорция в архитектуре
Загадки
египетских
пирамид
Слайд 15Золотое соотношение мы можем увидеть и в здании собора Парижской
Богоматери (Нотр-дам де Пари)
Слайд 16 Долгое время считали, что зодчие
Древней Руси строили все
«на глазок»,
без особых математических расчетов.
Однако новейшие исследования
показали, что русские архитекторы хорошо знали математические пропорции, о чем свидетельствует анализ геометрии
древних храмов
Слайд 17
Золотые пропорции
широко использовалв своем творчестве
М.Ф.Казаков
Петровский дворец
Дом Пашкова
Золотые пропорции в архитектуре
Слайд 19В особый вид изобразительного искусства Древней Греции следует выделить изготовление
и роспись всевозможных сосудов. В изящной форме легко угадываются пропорции
золотого сечения .Слайд 20Переходя к примерам “золотого сечения” в живописи, нельзя не остановить
своего внимания на творчестве Леонардо да Винчи.
Сам термин “золотое сечение”
ввел Леонардо да Винчи. Он говорил о пропорции человеческого тела.“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Слайд 22Нет живописи более поэтичней,чем живопись Боттичелли Сандро, и нет у
великого Сандро картины более знаменитой, чем его “Венера”. Для Боттичелли
его Венера – это воплощение идеи универсальной гармонии “золотого сечения”, господствующего в природе.Пропорциональный анализ Венеры убеждает нас в этом
Слайд 23
Рафаэль Санти «Афинская школа»
При построении комбинации треугольников использовано золотое сечение.
Рафаэль Санти «Афинская школа»При построении комбинации треугольников использовано золотое сечение.
Слайд 24Рафаэль Санти не был ученым-математиком, но подобно многим художникам эпохи
Возрождения, обладал немалыми познаниями в геометрии. В знаменитой фреске «Афинская
школа», где в храме науки собралось общество великих философов древности, наше внимание привлекает группа Евклида – крупнейшего древнегреческого математика, разбирающего хитроумный чертеж.Хитроумная комбинация двух треугольников также построена в соответствии с пропорцией золотого сечения: она может быть вписана в треугольник с соотношением сторон 5/8. Это удивительно легко вставляется в верхний участок живописной архитектуры. Верхний угол треугольника упирается в замковый камень арки на ближнем к зрителю участке, нижний - в точку схода перспектив, а боковой участок обозначает пропорции пространственного разрыва между двумя частями арок. И не случайно в облике живописного Эвклида обнаруживается портрет друга Рафаэля, известного архитектора Браманте, участвовавшего в разработке проекта Сикстинской капеллы. Это здание создавалось согласно тем математическим и художественным законам, которые установлены персонажами фрески - учёными античного мира.
Слайд 25Золотое сечение в картине И. И. Шишкина"Сосновая роща"
На этой знаменитой
картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения.
Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.Слайд 26И.Е.Репин «А.С.Пушкин на акте в Лицее
8 января 1815 года»
Фигура Пушкина
помещена
художником в правой части
картины по линии золотого
сечения.
Левая
часть картины тоже разделена в пропорциях золотого сечения: от головы Пушкина до головы Державина и от нее до левого края картины.Слайд 27 Н.Ге «А.С.Пушкин в селе Михайловском»
Фигура А.С.Пушкина поставлена
художником слева
на линии
золотого сечения
Слайд 28В.Суриков «Боярыня Морозова»
Роли боярыни отведена
средняя часть картины.
Она окована
точкой высшего
взлета и точкой низшего
спадания сюжета картины.
Это
взлет руки Морозовойс двуперстным крестным
знамением как высшая точка
2)Это беспомощно протянутая
к боярыне рука старухи-нищей
странницы.
Сечение А1В1, отстоящее на 0.168… от правого края картины проходит не через руку, а оказывается где-то перед
ртом боярыни!
Золотое сечение А1В1 проходит по слову, которое летит из уст боярыни Морозовой.
Ибо не рука, не горящие глаза, не рот — здесь главное. Но огненное слово фанатического убеждения.
В нём, и именно в нём, — величайшая сила Морозовой.
Слайд 29Максимальная громкость звука , которая начинает вызывать болевые ощущения, равна
130 децибелам.
Разделим 130:1,618= 80 децибел? Которые характерны для громкости человеческого
крика80:1,618= 50 –соответствует громкости человеческой речи
50:2,618 (квадрат золотой пропорции) =20 –соответствует шепоту человека
Громкость звука
Слайд 30музыка есть арифметическое упражнение души,которая исчисляет себя, не зная об
этом
ЛейбницМатематическая теория музыки пифагорейцев явилась первой теорией музыки у греков. Пифагор видел в музыке могучее средство воспитания. Пифагорейский музыкальный строй, определивший на столетия судьбу европейской музыки – это математика. Создание логарифмически равномерной 12-тонной музыкальной шкалы – итог совместной деятельности музыкантов и математиков. В 17в. в теории сохранялась точка зрения, что музыка – это теория о числах. т.е. раздел математики.
Слайд 31Алгебра музыки
В композиции многих музыкальных произведений отмечается наличие высшей
точки, некоторого
«кульминационного взлета», причем это характерно не только для произведения в
целом, но и для отдельных его частей. Такая точка крайне редко расположена в центре произведения, обычно она смещена, ассиметрична. Во многих произведениях Бетховена, Шопена, Скрябина эта высшая точка приходится на сильную долю шестого такта или на последнюю мелкую долю пятого такта, т .е. находится в точке золотого сечения.Слайд 32Наибольшее количество музыкальных произведений, в которых имеется
золотое сечение у
Аренского (95%)
Шопена (92%)Бетховена (97%)
Шуберта (91%)
Гайдна (97%)
Скрябина(90%)
Моцарта (91%)
Слайд 33ученый М.А.Марутаев подсчитал количество тактов в знаменитой сонате "Аппассионата" и
нашел ряд интересных числовых соотношений.
В частности, в разработке –
центральной структурной единице сонаты, где интенсивно развиваются темы и сменяют друг друга тональности, - два основных раздела. В первом 43,25 такта, во втором – 26,75.Отношение 43,25:26,75=0,618:0,382=1,618 дает золотое сечение.
Бетховен "Аппасионата"
Слайд 34Поэзия А.С.Пушкина- образец наиболее выдающихся творений мировой культуры, образец высочайшего
уровня гармонии
Чувство гармонии у Пушкина было развито необычайно, что объективно
подтверждает гениальность великого поэта и писателя.Для анализа метрики стихотворений А.С.Пушкина рассмотрены его стихи периода 1829-1836гг. Сюда вошло 109 произведений. Число строк в стихотворениях этого периода изменялось от 4 до 116. Средний размер этих стихотворений составил 88 строк.
Но размеры стихов распределены не равномерно. В них отчетливо выделяются несколько максимумов - наиболее встречающихся размеров. Они тяготеют к числам 5,8,13,21, 34. Автор явно предпочитает стихи, размер которых близок к числам Фибоначчи.
Музыка стихов
Слайд 35Примеры из поэзии бесчисленны. Особенно ими изобилует Пушкин. Беру наугад
два любимых наиболее ярких образца: в них попадания золотого сечения
в самих стихах отбиты знаком полной остановки — точкой, которая попадается внутри стиха только в месте золотого сечения.Пример взят из второй песни «Руслана и Людмилы»:
С порога хижины моей
Так видел я, средь летних дней,
Когда за курицей трусливой
Султан курятника спесивый,
Петух мой по двору бежал
И сладострастными крылами
Уже подругу обнимал;
Над ними хитрыми кругами
Цыплят селенья старый вор,
Прияв губительные меры,
Носился, плавал коршун серый
И пал как молния на двор.
Взвился, летит. || В когтях ужасных
Во тьму расселин безопасных
Уносит бедную злодей.
Напрасно, горестью своей
И хладным страхом пораженный,
Зовет любовницу петух...
Он видит лишь летучий пух,
Летучим ветром занесенный.
(«Руслан и Людмила», 1817—1820. Песнь вторая)
Золотое сечение проходит по тринадцатому стиху (из двадцати), разрезая его на два массива словесного материала, из которых больший — точно 0,62 всего объёма (золотое сечение: 0,618).
Слайд 36Представляет несомненный интерес анализ романа "Евгений
Онегин", сделанный Н. Васютинским.
Этот роман состоит из 8 глав, в каждой из них
в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава.
В ней 51 стих.
Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!
Н. Васютинский констатирует:
"Кульминацией главы является объяснение Евгения в любви к Татьяне - строка "Бледнеть и гаснуть ... вот блаженство!".
Эта строка делит всю восьмую главу на две части - в первой 477 строк, а во второй - 295 строк.
Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!".
Золотое сечение в поэзии
Слайд 37
Кульминационный момент
- сцена в спальне графини, куда проник Германн в надежде
узнать тайну трех карт.В повести 853 строки.
Кульминация – смерть графини -535 строка.
853:535=1,6 –точное
место золотого сечения повести
Вторая глава повести содержит 219 строк. Золотое сечение приходится в ней на 135 строку –это кульминация главы- Лиза увидела в окне стоящего Германна- отсюда и начался новый отсчет времени
219:135=1,62.
Третья глава -212 строк.Кульминация усилий Германна проникнуть в дом старой графини приходится на 131 строку
212:131= 1.63
В четвертой главе 113 строк золотая пропорция приходится на 70 строку –трагический момент для Лизы
В пятой главе(75 строк) –посещение Германном похорон графини, 46 строка делит повествование на похороны графини и сон Германна
75:46= 1.63
В последней главе золотая пропорция приходится на 77 строку –завершение описания первого дня игры Германна в карты и первого его выигрыша
Композиция "Пиковой дамы" А.С.Пушкина
Слайд 38Поверить алгеброй гармонию
Знаменитое стихотворение Лермонтова "Бородино" делится на две части:
вступление, обращенное к рассказчику и занимающее лишь одну строфу ("Скажите,
дядя, ведь недаром..."), и главную часть, представляющее самостоятельное целое, которое распадается на две равносильные части.В первой из них описывается с нарастающим напряжением ожидание боя, во второй - сам с постепенным снижением напряжения к концу стихотворения.
Граница между этими частями является кульминационной точкой произведения и приходится как раз на точку деления его золотым сечением.
Главная часть стихотворения состоит из 13 семистиший, то есть из 91 строки. Разделив ее золотым сечением (91:1,618 = 56,238), убеждаемся, что точка деления находится в начале 57-го стиха, где стоит короткая фраза: "Ну ж был денек!".
Именно эта фраза представляет собой "кульминационный пункт возбужденного ожидания", завершающей первую часть стихотворения (ожидание боя) и открывающий вторую его часть (описание боя).
Таким образом, золотое сечение играет в поэзии весьма осмысленную роль, выделяя кульминационный пункт стихотворения.
Слайд 39Сенсационное открытие сделал петербургский поэт и переводчик “Слова о полку
Игореве” Андрей Чернов. Он нашел, что построение стихов загадочного древнерусского
памятника подчиняется математическим законам. Исследования позволили сделать Чернову заключение о том, что в основу “Слова о полку Игореве”, состоящего из девяти песен, легла круговая композиция.А поводом к тому, чтобы проверить гармонию поэму алгеброй, послужила статья о жизни древнегреческого математика Пифагора. Внимание Чернова привлекли рассуждения о “золотом сечении” и о числе , которые восходят к Пифагору. Возникла неожиданная ассоциация: ведь в композиционном построении поэму тоже круг и, следовательно, должны быть “диаметр” и некая математическая закономерность.
Уже первые расчеты стали подтверждать закономерность, да еще какую! Если число стихов во всех трех частях (их 804) разделить на число стихов в первой и последней части (256), получается 3,14, т.е. число с точностью до третьего знака.
Открытие Чернова приводят к естественному вопросу: как древний автор “Слова о полку Игореве”, ничего не зная о числе , ни о других математических формулах, привнес организующее математическое начало в этот текст? Чернов предполагает, что автор использовал это интуитивно, подчиняясь образам древнегреческих архитектурных памятников. В те времена храм являл собой всеобъемлющий, художественный идеал, поэтому влиял на ритмику поэтического самовыражения.
Слайд 40 Золотое сечение в фотографии
Принято считать, что объекты,
содержащие в
себе золотое сечение,
воспринимаются как наиболее
Гармоничные. Примером использования
правил
золотой пропорции в фотографии может являться
Расположение объекта в особых точках-
«зрительных центрах»
Часто используются точки,
расположенные на расстоянии3/8 и
5/8 от соответствующих краев
плоскости
Слайд 41Т.е.расположение основных компонентов
кадра в особых точках-зрительных центрах.
Зритель всегда акцентирует
свое внимание
на этих точках, независимо от формата кадра
В фотографии
правило золотого сеченияподразумевает расположение объектов
съемки не по центру кадра, а предполагает
соподчинение объектов композиции
с распределением площадей 3:8+5:8 для
2 –х предметов