Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. ЕГЭ - 2017
Содержание
- 1. Математика. ЕГЭ - 2017
- 2. ЗАДАНИЕ №11 - 1Смешав 25 % и
- 3. ЗАДАНИЕ №11 - 2Имеется два сплава. Первый
- 4. ЗАДАНИЕ №11 - 3От пристани А к
- 5. ЗАДАНИЕ №11 - 4 Первая труба пропускает
- 6. ЗАДАНИЕ №11 - 5Изюм получается в процессе
- 7. ЗАДАНИЕ №11 - 6Два гонщика участвуют в
- 8. ЗАДАНИЕ №11 - 7 Из пункта А
- 9. ЗАДАНИЕ №11 - 8 Путешественник переплыл
- 10. ЗАДАНИЕ №11 - 9 Моторная лодка
- 11. ЗАДАНИЕ №11 - 10 Коля и
- 12. ЗАДАНИЕ №11 - 11 Игорь и
- 13. ЗАДАНИЕ №11 - 12 По двум
- 14. РЕШЕНИЕ №11-1 x кг – масса
- 15. РЕШЕНИЕ №11 - 2Пусть x кг –
- 16. РЕШЕНИЕ №11 - 3Х км/ч– скорость первого,
- 17. РЕШЕНИЕ №11-4Пропускную способность первой трубы обозначим через
- 18. РЕШЕНИЕ №11-5 Сухого вещества изюма в
- 19. РЕШЕНИЕ №11-6Пусть х - скорость первого гонщика, а у - скорость
- 20. РЕШЕНИЕ №11-7Обозначим через х скорость первого автомобиля. Через S половину
- 21. РЕШЕНИЕ №11-8 1-й способ. Средняя скорость будет равна,
- 22. РЕШЕНИЕ №11-9Пусть скорость моторной лодки в неподвижной
- 23. РЕШЕНИЕ №11-10Пусть в тесте х вопросов. Тогда общее
- 24. РЕШЕНИЕ №11-11Пусть за х часов красит забор Игорь, за у часов
- 25. РЕШЕНИЕ №11-12 Скорость обгона пассажирским
- 26. ИСТОЧНИКИ: 1. Автор шаблона: Гусева Наталья
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Автор: учитель математики
высшей категории
Молодых Елена Николаевна
МКОУ «Хлопуновская СОШ»
Шипуновский
район
Слайд 2ЗАДАНИЕ №11 - 1
Смешав 25 % и 95 % растворы
кислоты и добавив 20 кг чистой воды, получили 40 %
раствор кислоты. Если бы вместо 20 кг воды добавили 20 кг 30 % раствора той же кислоты, то получили бы 50 % раствор кислоты. Сколько килограммов 25 % раствора использовали для получения смеси?РЕШЕНИЕ
Слайд 3ЗАДАНИЕ №11 - 2
Имеется два сплава. Первый содержит 15% никеля,
второй — 45% никеля. Из этих двух сплавов получили третий
сплав массой 24 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была больше массы второго?РЕШЕНИЕ
Слайд 4ЗАДАНИЕ №11 - 3
От пристани А к пристани В, расстояние
между которыми равно 153 км, отправился с постоянной скоростью первый
теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.Ответ дайте в км/ч.
РЕШЕНИЕ
Слайд 5ЗАДАНИЕ №11 - 4
Первая труба пропускает на 8 литров
воды в минуту меньше, чем вторая. Сколько литров воды в
минуту пропускает первая труба, если резервуар объёмом 180 литров она заполняет на 8 минут дольше, чем вторая труба?РЕШЕНИЕ
Слайд 6ЗАДАНИЕ №11 - 5
Изюм получается в процессе сушки винограда. Сколько
килограммов винограда потребуется для получения 54 килограммов изюма, если виноград
содержит 90% воды, а изюм содержит5% воды?
РЕШЕНИЕ
Слайд 7ЗАДАНИЕ №11 - 6
Два гонщика участвуют в гонках. Им предстоит
проехать 68 кругов по кольцевой трассе протяжённостью 6 км. Оба
гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 15 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 60 минут? Ответ дайте в км/ч.РЕШЕНИЕ
Слайд 8ЗАДАНИЕ №11 - 7
Из пункта А в пункт В
одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь
путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 72 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 45 км/ч. Ответ дайте в километрах в час.РЕШЕНИЕ
Слайд 9ЗАДАНИЕ №11 - 8
Путешественник переплыл океан на яхте
со средней скоростью 26 км/ч. Обратно он летел на самолёте
со скоростью 312 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в километрах в час.РЕШЕНИЕ
Слайд 10ЗАДАНИЕ №11 - 9
Моторная лодка прошла против течения
реки 77 км и вернулась в пункт отправления, затратив на
обратный путь на 4 ч меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в километрах в час.РЕШЕНИЕ
Слайд 11ЗАДАНИЕ №11 - 10
Коля и Митя выполняют одинаковый
тест. Коля отвечает за час на 12 вопросов теста, а
Митя — на 21. Они одновременно начали отвечать на вопросы теста, и Коля закончил свой тест позже Мити на 105 минут. Сколько вопросов содержит тест?РЕШЕНИЕ
Слайд 12ЗАДАНИЕ №11 - 11
Игорь и Паша красят забор
за 18 часов. Паша и Володя красят этот же забор
за 24 часа, а Володя и Игорь — за 36 часов. За сколько часов мальчики покрасят забор, работая втроём?РЕШЕНИЕ
Слайд 13ЗАДАНИЕ №11 - 12
По двум параллельным железнодорожным путям
в одном направлении следуют пассажирский и товарный поезда, скорости которых
равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.РЕШЕНИЕ
Слайд 14РЕШЕНИЕ №11-1
x кг – масса 25% раствора, y
кг – масса 95% раствора.
- суммарная масса. - 40% раствор.Так как масса кислоты после добавления остается прежней, то имеем уравнение
Аналогично . Решаем систему
Ответ : 20
Слайд 15РЕШЕНИЕ №11 - 2
Пусть x кг – масса первого сплава,
а y кг – масса второго сплава. Тогда, масса никеля
в первом сплаве равна 0,15х, а масса никеля во втором сплаве – 0,45у. Сказано, что из этих двух сплавов можно получить третий массой 24 кг с 20% никелем, то есть масса никеля в третьем сплаве равна . Получаем уравнение: При этом: Имеем систему уравнений:Ответ: 16
Слайд 16РЕШЕНИЕ №11 - 3
Х км/ч– скорость первого, тогда (х +
8) км/ч– второго. Вместе прошли 153 км
ч – затратил первый теплоход, а ч – второй. илиРешаем квадратное уравнение,
получим
Ответ: 9
Слайд 17РЕШЕНИЕ №11-4
Пропускную способность первой трубы обозначим через х. Тогда вторая
труба будет пропускать х + 8 литров воды. Время заполнения объема
в 180 литров первой трубы составляет , а тот же объем для второй трубыПо условию задачи сказано, что вторая труба заполняет данный объем на 8 минут быстрее первой. Получаем уравнение
Решаем квадратное уравнение,
получим
Ответ: 10
Слайд 18РЕШЕНИЕ №11-5
Сухого вещества изюма в 54 килограммах равно
Объем винограда обозначим через Х . Тогда сухого
вещества винограда будетСухого вещества винограда и изюма должны быть равны, т.е. получаем уравнение
Ответ: 513.
Слайд 19РЕШЕНИЕ №11-6
Пусть х - скорость первого гонщика, а у - скорость второго гонщика. Они
оба проехали 68 кругов по 6 км каждый круг, т.е.
расстояние 408 км. Время первого гонщика составило , а время второго . Известно, чтопервый гонщик пришел на 15 минут раньше второго, т.е. на 1/4 часа быстрее, получаем уравнение
Также в задаче сказано, что первый гонщик впервые обогнал на круг (на 6 км) второго через 60 минут (1 час), следовательно,
Получаем систему уравнений
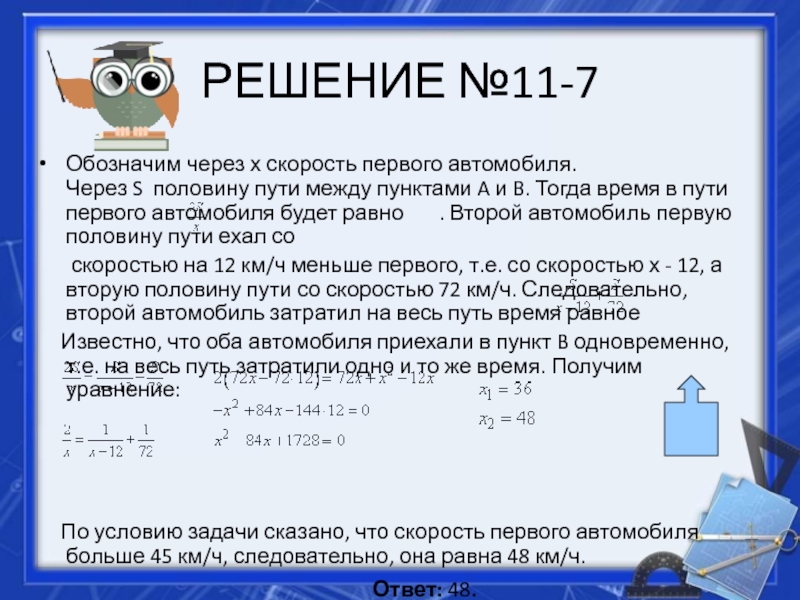
Ответ: 96
Слайд 20РЕШЕНИЕ №11-7
Обозначим через х скорость первого автомобиля. Через S половину пути между пунктами
A и B. Тогда время в пути первого автомобиля будет
равно . Второй автомобиль первую половину пути ехал соскоростью на 12 км/ч меньше первого, т.е. со скоростью х - 12, а вторую половину пути со скоростью 72 км/ч. Следовательно, второй автомобиль затратил на весь путь время равное
Известно, что оба автомобиля приехали в пункт B одновременно, т.е. на весь путь затратили одно и то же время. Получим уравнение:
По условию задачи сказано, что скорость первого автомобиля больше 45 км/ч, следовательно, она равна 48 км/ч.
Ответ: 48.
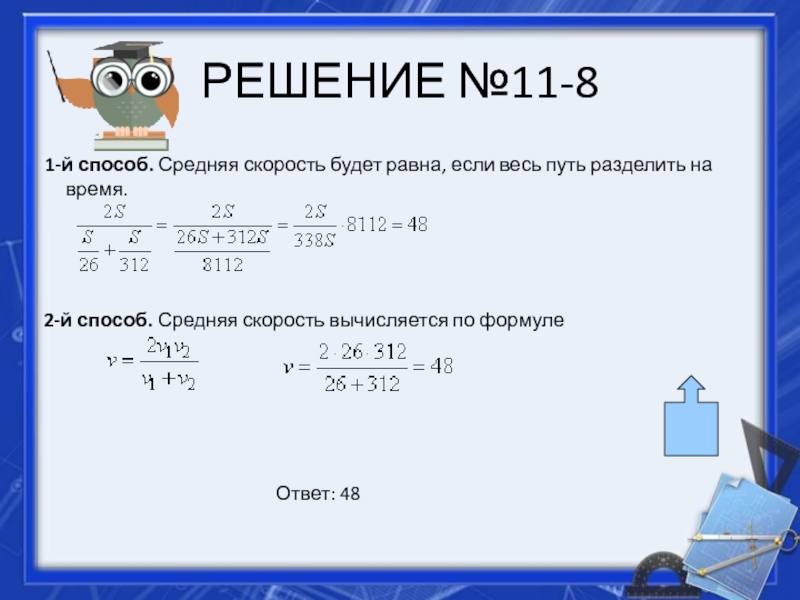
Слайд 21РЕШЕНИЕ №11-8
1-й способ. Средняя скорость будет равна, если весь путь
разделить на время.
2-й способ. Средняя скорость вычисляется по формуле
Ответ: 48Слайд 22РЕШЕНИЕ №11-9
Пусть скорость моторной лодки в неподвижной воде равна х км/ч. Тогда
скорость лодки против течения будет равна (х – 2) км/ч. Расстояние в
77 км лодка преодолеет с такой скоростью за часа. На обратном пути лодка шлапо течению, следовательно, со скоростью (х + 2) км/ч и прошла 77 км за часа.
В задаче сказано, что на обратный путь было потрачено на 4 часа меньше, получаем уравнение
Ответ: 9
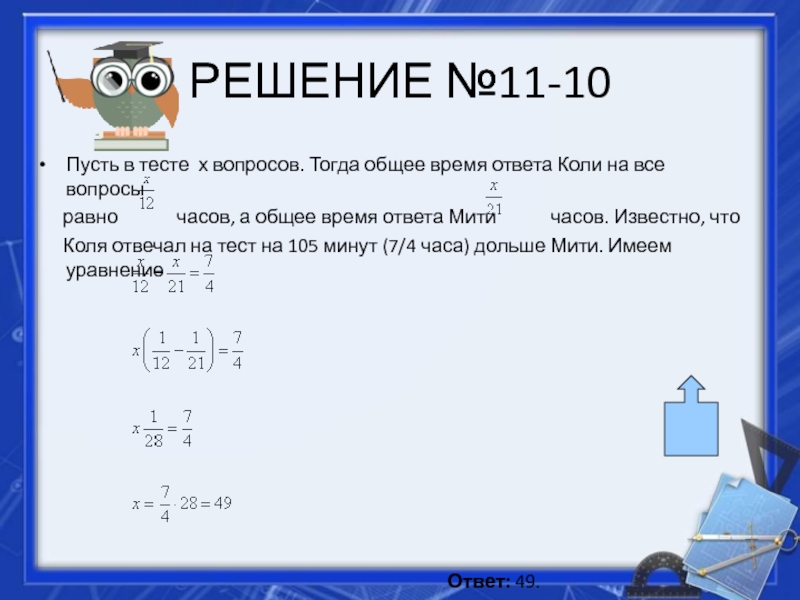
Слайд 23РЕШЕНИЕ №11-10
Пусть в тесте х вопросов. Тогда общее время ответа Коли
на все вопросы
равно
часов, а общее время ответа Мити часов. Известно, что Коля отвечал на тест на 105 минут (7/4 часа) дольше Мити. Имеем уравнение
Ответ: 49.
Слайд 24РЕШЕНИЕ №11-11
Пусть за х часов красит забор Игорь, за у часов - Паша, а
за z часов Володя. Весь забор условно примем за одну целую часть,
т.е. за 1. В задаче сказано, что Игорь и Паша вместе красят забор за 18 часов, т.е. можем записать уравнениеАналогично для Паши и Володи
и Володи и Игоря
Получаем систему из трех уравнений
Ответ: 16.
Слайд 25РЕШЕНИЕ №11-12
Скорость обгона пассажирским поездом товарного составляет
80-50=30 км/ч. Товарный поезд имеет длину 1200 метров или 1,2
км. В задаче сказано, что пассажирский поезд прошел мимо товарного за 3 минуты (за 1/20 часа) со скоростью 30 км/ч. То есть была пройдена вся длина товарного поезда и еще длина самого пассажирского поезда. Обозначим через х длину пассажирского поезда, тогда расстояние равное х + 1,2 было пройдено за 1/20 часа со скоростью 30 км/ч. Получаем уравнениеТо есть длина пассажирского поезда равна 0,3 км или 300 метров.
Ответ: 300
Слайд 26ИСТОЧНИКИ:
1. Автор шаблона: Гусева Наталья Андреевна зам. директора
по ВР
школа – лицей №4 г.Рудный http://pedsovet.su/load/412-1-0-45829
2. ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под ред. И. В. Ященко. — М. : Издательство «Национальное образование», 2017.
3. Рисунки: ЕГЭ http://teplystan.mos.ru/upload/medialibrary/c52/egeh.png
Сова http://sch-53.ru/files/teacher_24/sova.png