Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Медиана, биссектриса,высота треугольника"
Содержание
- 1. "Медиана, биссектриса,высота треугольника"
- 2. Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны. AK = KC , BK-медиана треугольника ABC ,
- 3. В любом треугольнике можно провести 3 медианы. Все они пересекаются в одной точке, в центре (центре тяжести) треугольника.
- 4. Биссектриса треугольника — отрезок биссектрисы угла треугольника, соединяющий
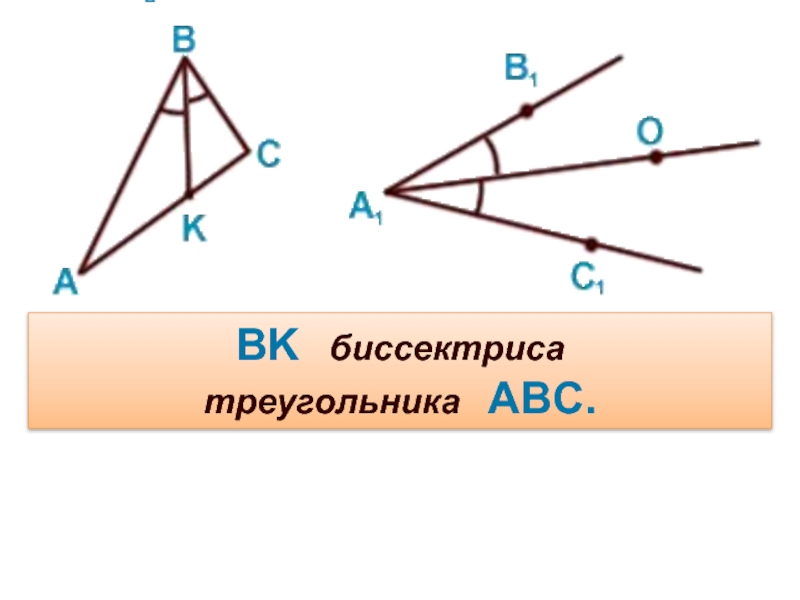
- 5. BK биссектриса треугольника ABC.
- 6. В каждом треугольнике можно провести 3 биссектрисы, которые
- 7. Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
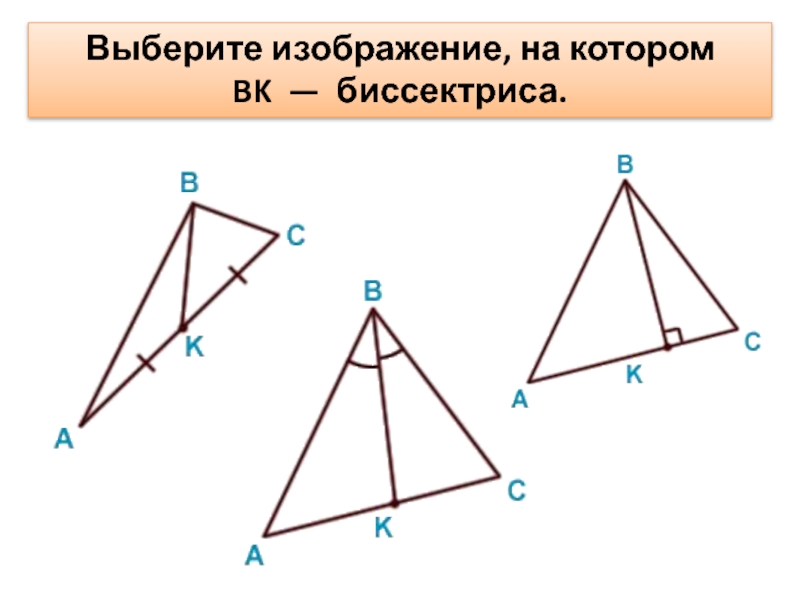
- 8. Выберите изображение, на котором BK — биссектриса.
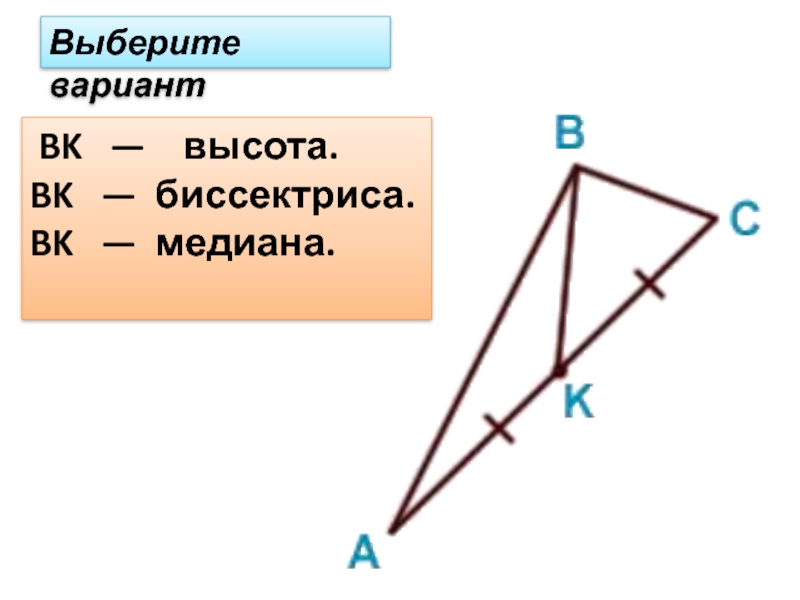
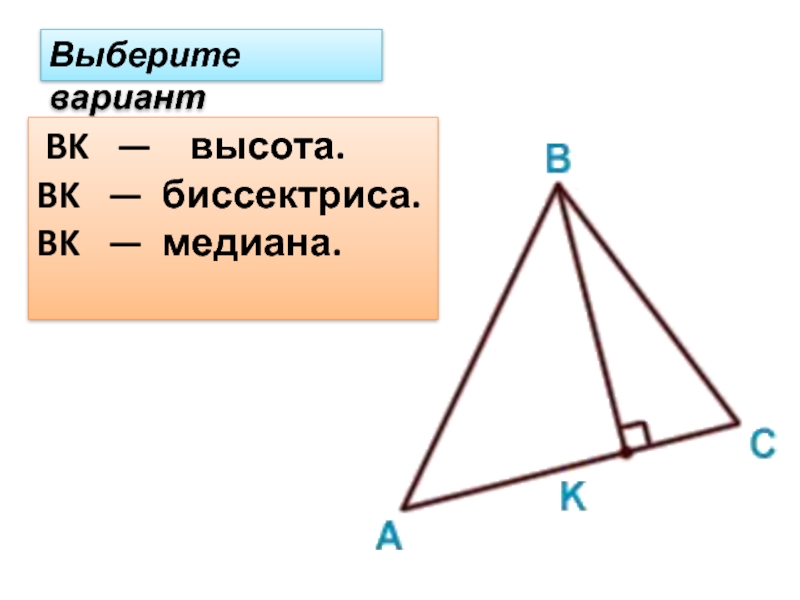
- 9. Выберите вариант BK — высота. BK — биссектриса. BK — медиана.
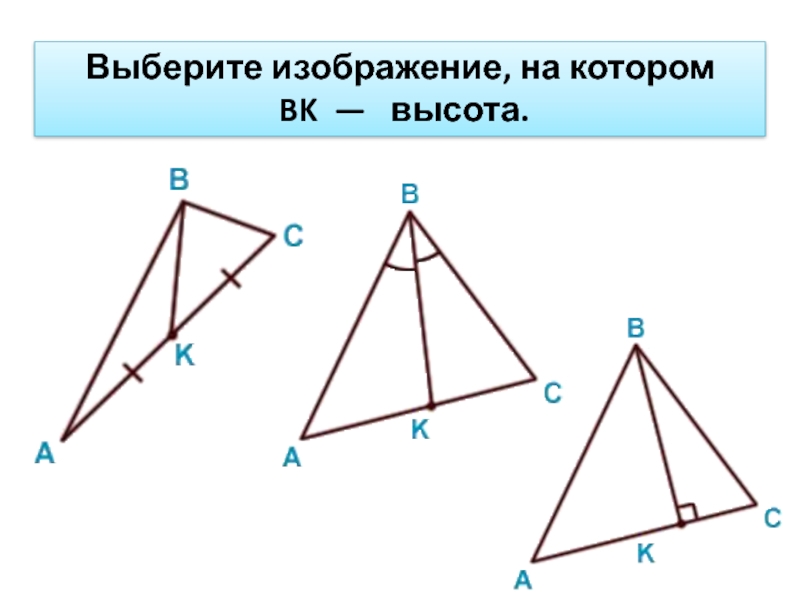
- 10. Выберите изображение, на котором BK — высота.
- 11. Выберите вариант BK — высота. BK — биссектриса. BK — медиана.
- 12. Точка К лежит на стороне АС треугольника
- 13. Точка М середина АС, стороны треугольника АВС
- 14. Школьный помощник - учебники онлайн, правила, задачи, примеры
- 15. Скачать презентанцию
Медиана треугольника — отрезок, соединяющий вершину треугольника с серединой противоположной стороны. AK = KC , BK-медиана треугольника ABC ,
Слайды и текст этой презентации
Слайд 2Медиана треугольника —
отрезок, соединяющий вершину
треугольника с серединой противоположной стороны.
AK
= KC ,
BK-медиана
Слайд 3В любом треугольнике можно провести 3 медианы.
Все они пересекаются в одной
точке,
в центре (центре тяжести) треугольника.
Слайд 4Биссектриса треугольника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой
на противолежащей стороне.
биссектриса угла — это луч, делящий угол
на два равных,
а биссектриса треугольника — это отрезок, часть луча,
ограниченная стороной треугольника. 
Слайд 6В каждом треугольнике можно провести
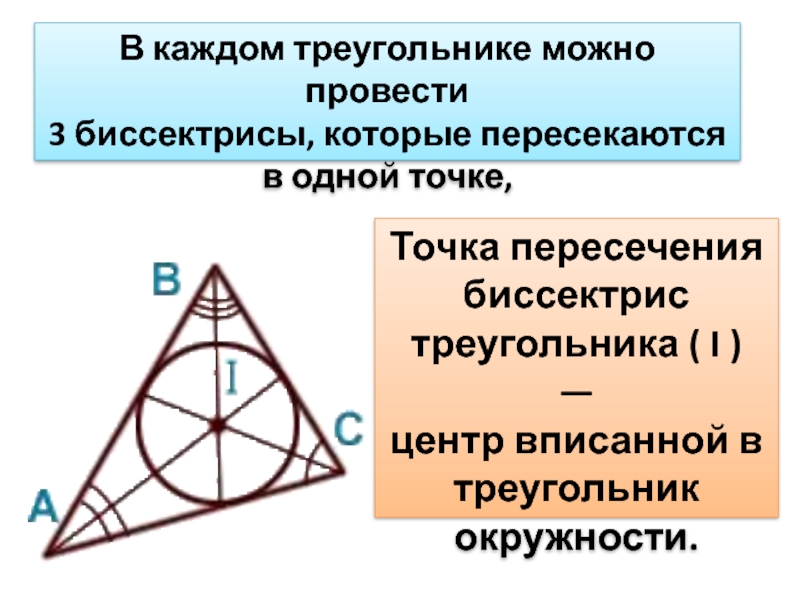
3 биссектрисы, которые пересекаются в одной точке,
Точка пересечения
биссектрис треугольника ( I ) —
центр вписанной в треугольник
окружности.
Слайд 7Высота треугольника — перпендикуляр, проведенный
из вершины треугольника к прямой, содержащей противоположную
сторону.
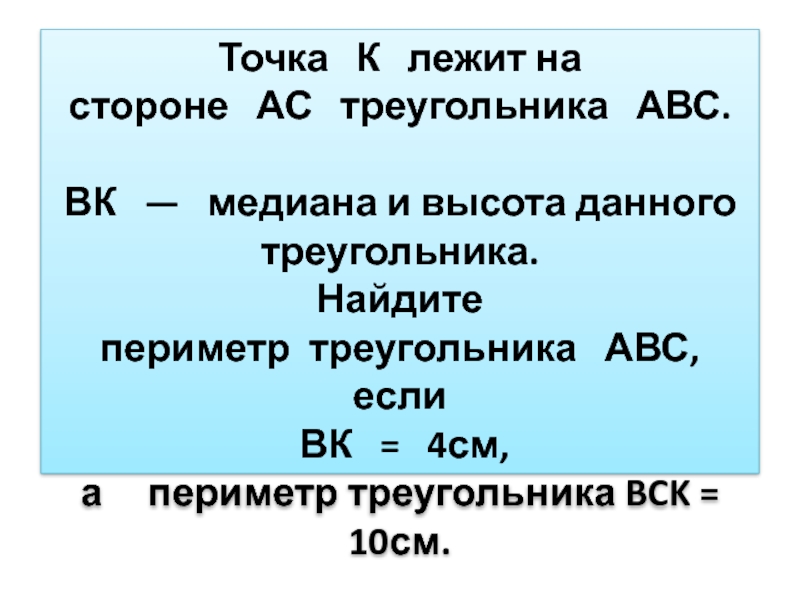
Слайд 12Точка К лежит на стороне АС треугольника АВС.
ВК
— медиана и высота данного
треугольника.
Найдите периметр треугольника
АВС, если ВК = 4см, а периметр треугольника BCK = 10см.
Слайд 13Точка М середина АС,
стороны треугольника АВС и ВМ —
высота треугольника АВС.
ВК - биссектриса угла АВМ. Найдите
угол АВС, если угол КВМ = 17°. 
