Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод графов
Содержание
- 1. Метод графов
- 2. ВведениеГрафы заинтересовали нас своей возможностью помогать в
- 3. С дворянским титулом «граф» тему нашей работы
- 4. История возникновения графовТермин "граф" впервые появился в
- 5. Что такое графСлово «граф» в математике означает
- 6. В математике определение графа дается так:Графом называется
- 7. В каждой вершине графа сходятся несколько линий
- 8. Основы теории графов как математической науки заложил
- 9. Задача о Кенигсбергских мостахБывший Кенигсберг (ныне Калининград)
- 10. Так возникла задача-головоломка: «можно ли пройти все
- 11. дальшеЯ здесь уже был!
- 12. В 1735 году задача стала известна Леонарду
- 13. Задача о Кенигсбергских мостах Граф можно начертить «одним
- 14. Одним росчеркомЕсли все вершины графа четные, то
- 15. Применение графовС помощью графов упрощается решение математических задач, головоломок, задач на смекалку.дальше
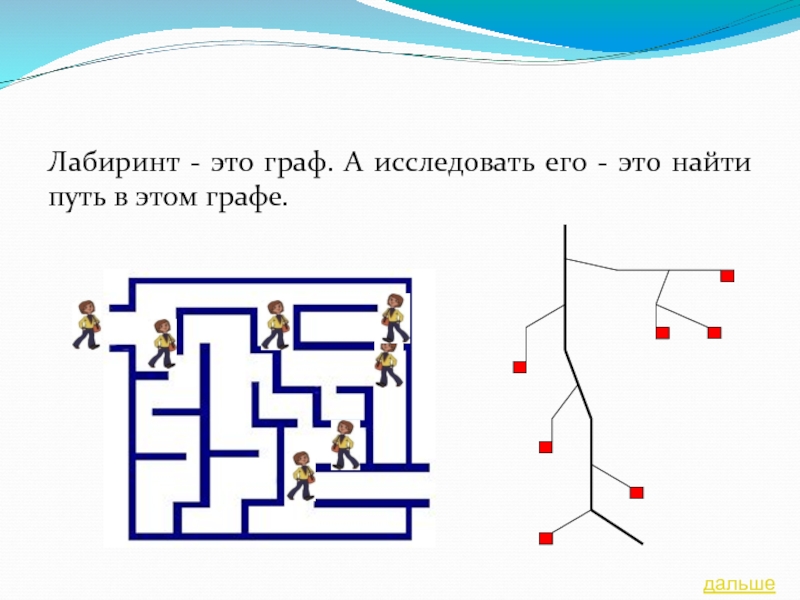
- 16. Лабиринт - это граф. А исследовать его - это найти путь в этом графе. дальше
- 17. Использует графы и дворянство.На рисунке приведена часть
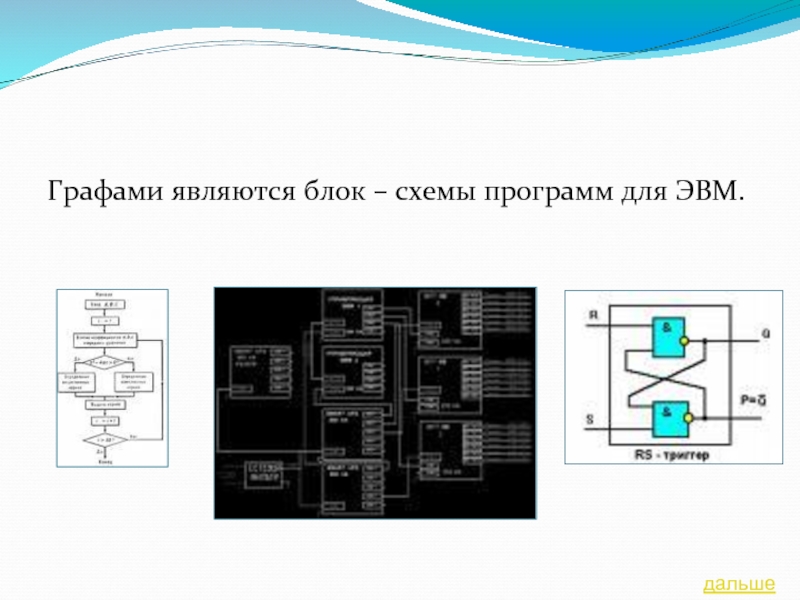
- 18. Графами являются блок – схемы программ для ЭВМ.дальше
- 19. Применение графовГрафами являются сетевые графики строительства.дальше
- 20. Типичными графами на географических картах являются изображения железных дорог.дальше
- 21. Применение графовТипичными графами на картах города являются схемы движения городского транспорта.дальше
- 22. Применение графовТипичными графами являются схемы авиалиний, которые часто вывешиваются в аэропортах.дальше
- 23. Применение графовГрафом является и система улиц города.
- 24. Применение графовГрафы есть и на картах звездного неба.дальше
- 25. Применение графовНа рисунке изображен граф, хорошо знакомый
- 26. Решите задачи
- 27. Нарисуйте граф, состоящий из четырех одноклассников:Саша и МашаСаша и ДашаМаша и ГришаГриша и Саша
- 28. Решение задачи
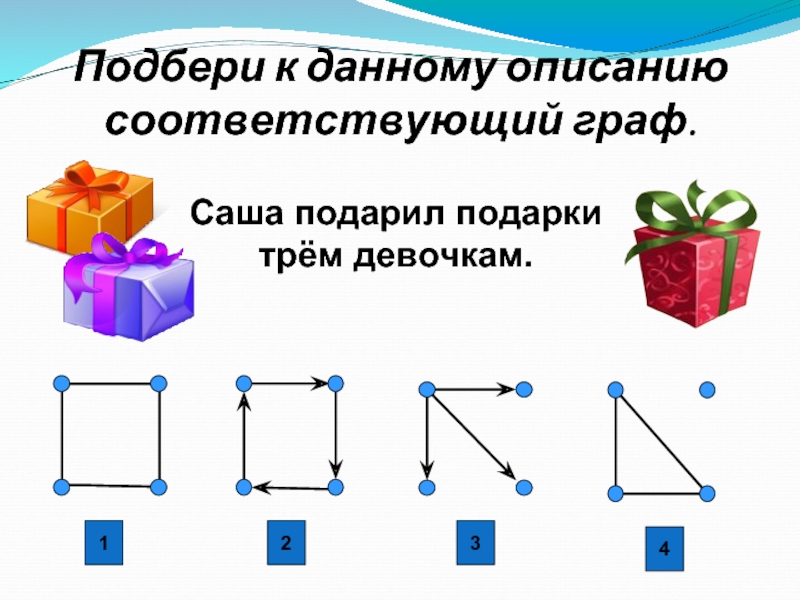
- 29. Подбери к данному описанию соответствующий граф. Саша подарил подарки трём девочкам.1234
- 30. Трое из четырех друзей сегодня говорили друг
- 31. Даша идет в гости к Грише и
- 32. Подбери к данному описаниюсоответствующий граф. Четыре друга
- 33. Между девятью планетами солнечной системы установлено
- 34. РешениеНарисуем схему условия: планеты изобразим точками, а
- 35. На рисунке изображено несколько контуров. Какие из
- 36. ВыводыГрафы – это замечательные математические объекты, с
- 37. Скачать презентанцию
ВведениеГрафы заинтересовали нас своей возможностью помогать в решении различных головоломок, математических и логических задач. Так как мы участвуем в математических олимпиадах, то теория графов была особенно актуальна в нашей подготовке. Мы
Слайды и текст этой презентации
Слайд 2Введение
Графы заинтересовали нас своей возможностью помогать в решении различных головоломок,
математических и логических задач. Так как мы участвуем в математических
олимпиадах, то теория графов была особенно актуальна в нашей подготовке. Мы решили разобраться какую роль в обычной жизни играют графы.содержание
Слайд 3
С дворянским титулом «граф» тему нашей работы связывает только общее
происхождение от латинского слова «графио» - пишу.
Г
Р
А
Ф
И
О
дальше
Слайд 4История возникновения графов
Термин "граф" впервые появился в книге венгерского математика
Д. Кенига в 1936 г., хотя начальные важнейшие теоремы о
графах восходят к Л. Эйлеру.Дальше
Слайд 5Что такое граф
Слово «граф» в математике означает картинку, где нарисовано
несколько точек, некоторые из которых соединены линиями. В процессе решения
задач математики заметили, что удобно изображать объекты точками, а отношения между ними отрезками или дугами.Дальше
Слайд 6
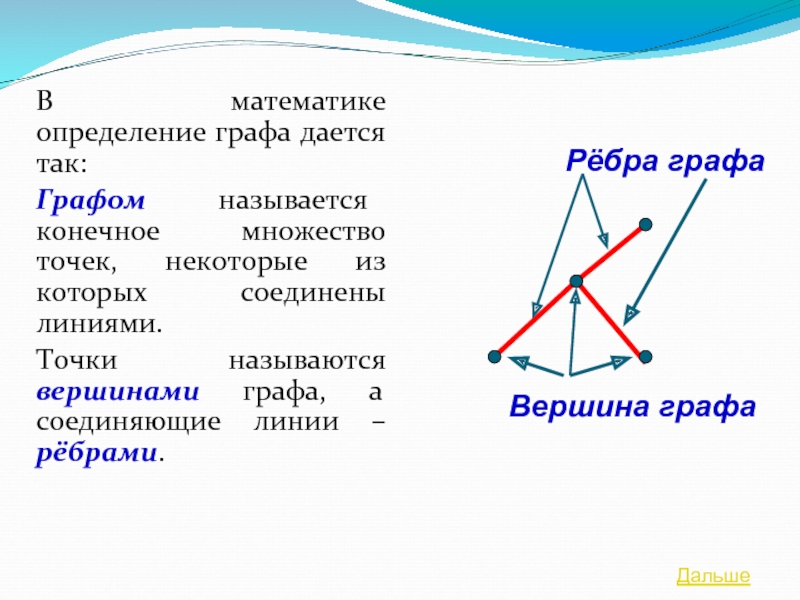
В математике определение графа дается так:
Графом называется конечное множество точек,
некоторые из которых соединены линиями.
Точки называются вершинами графа, а соединяющие
линии – рёбрами. Рёбра графа
Вершина графа
Дальше
Слайд 7
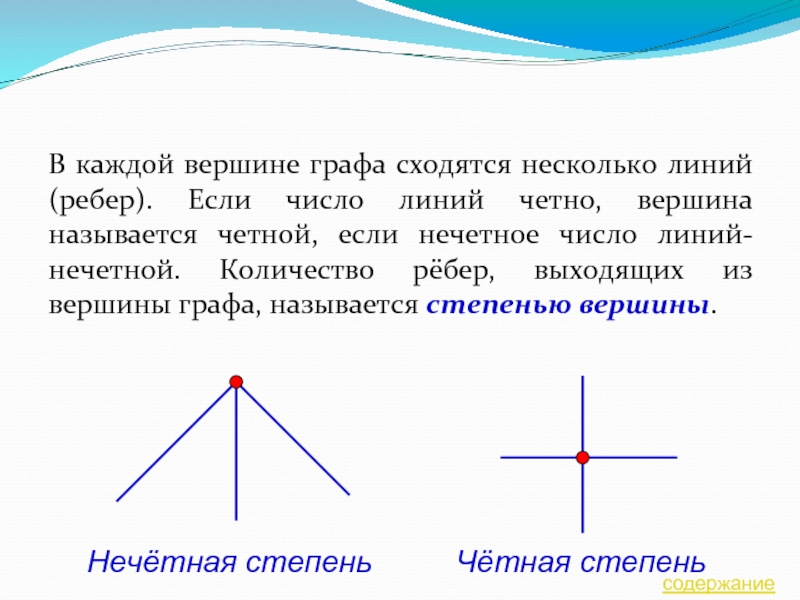
В каждой вершине графа сходятся несколько линий (ребер). Если число
линий четно, вершина называется четной, если нечетное число линий- нечетной.
Количество рёбер, выходящих из вершины графа, называется степенью вершины.Нечётная степень
Чётная степень
содержание
Слайд 8
Основы теории графов как математической науки заложил в 1736 г.
Леонард Эйлер, рассматривая задачу о Кенигсбергских мостах. Сегодня эта задача
стала классической.содержание
Слайд 9Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) стоит на реке
Преголь. Некогда там было семь мостов, которые связывали между собой
и с берегами два острова. Старые мосты не сохранились, но осталась карта города, где они изображены. Жители города заметили, что они никак не могут совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз.Дальше
Слайд 10
Так возникла задача-головоломка: «можно ли пройти все семь Кенигсбергских мостов
ровно один раз и вернуться в исходное место?»
Дальше
Слайд 12
В 1735 году задача стала известна Леонарду Эйлеру, который выяснил,
что пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение
по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.дальше
Слайд 13Задача о Кенигсбергских мостах
Граф можно начертить «одним росчерком» тогда и
только тогда, когда он содержит не более 2 нечетных вершин,
причем маршрут начинается в одной из таких вершин и заканчивается в другой. Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно.Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
содержание
Слайд 14Одним росчерком
Если все вершины графа четные, то можно не отрывая
карандаш от бумаги («одним росчерком»), проводя по каждому ребру только
один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.дальше
Слайд 15Применение графов
С помощью графов упрощается решение математических задач, головоломок, задач
на смекалку.
дальше
Слайд 17
Использует графы и дворянство.
На рисунке приведена часть генеалогического древа знаменитого
дворянского рода Л. Н. Толстого. Здесь его вершины – члены
этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.дальше
Слайд 21
Применение графов
Типичными графами на картах города являются схемы движения городского
транспорта.
дальше
Слайд 22Применение графов
Типичными графами являются схемы авиалиний, которые часто вывешиваются в
аэропортах.
дальше
Слайд 23Применение графов
Графом является и система улиц города. Его вершины –
площади и перекрестки, а ребра – улицы.
дальше
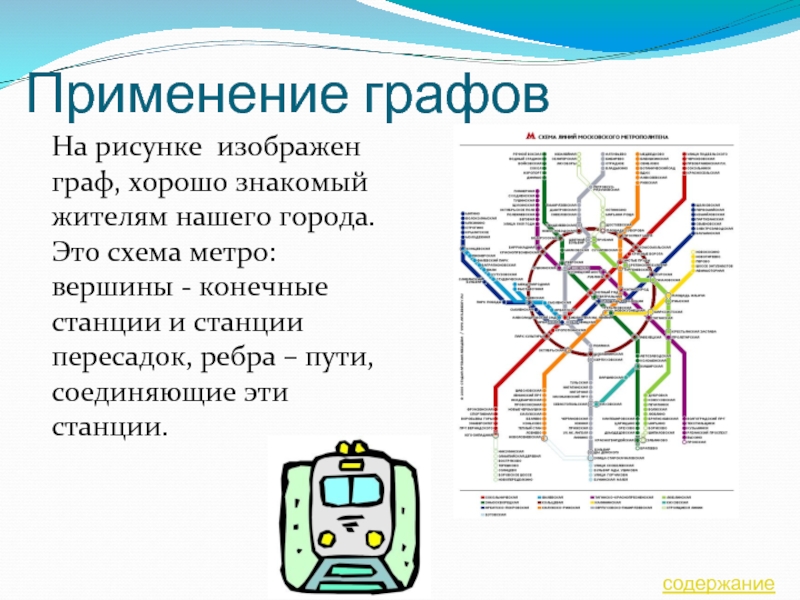
Слайд 25Применение графов
На рисунке изображен граф, хорошо знакомый жителям нашего города.
Это схема метро: вершины - конечные станции и станции пересадок,
ребра – пути, соединяющие эти станции.содержание
Слайд 27
Нарисуйте граф,
состоящий из четырех одноклассников:
Саша и Маша
Саша и Даша
Маша
и Гриша
Гриша и Саша
Слайд 30
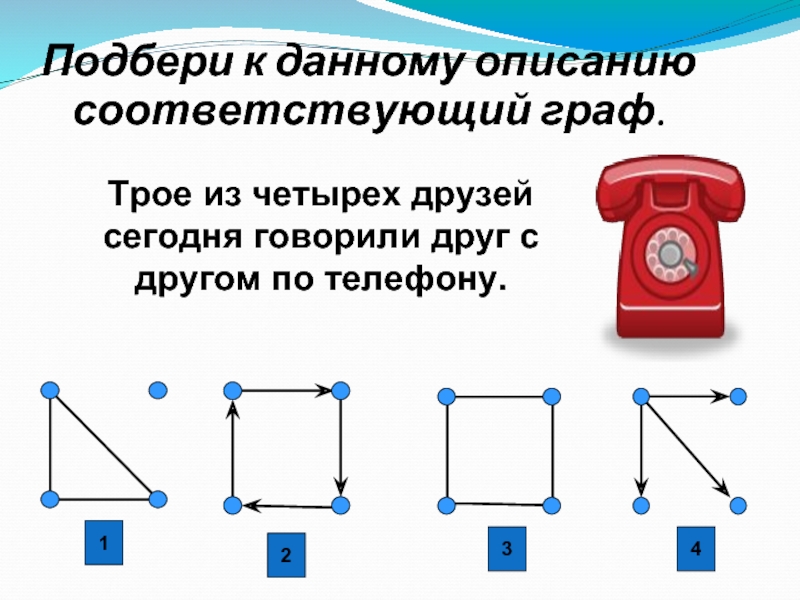
Трое из четырех друзей сегодня говорили друг с другом по
телефону.
Подбери к данному описанию
соответствующий граф.
2
3
4
1
Слайд 31
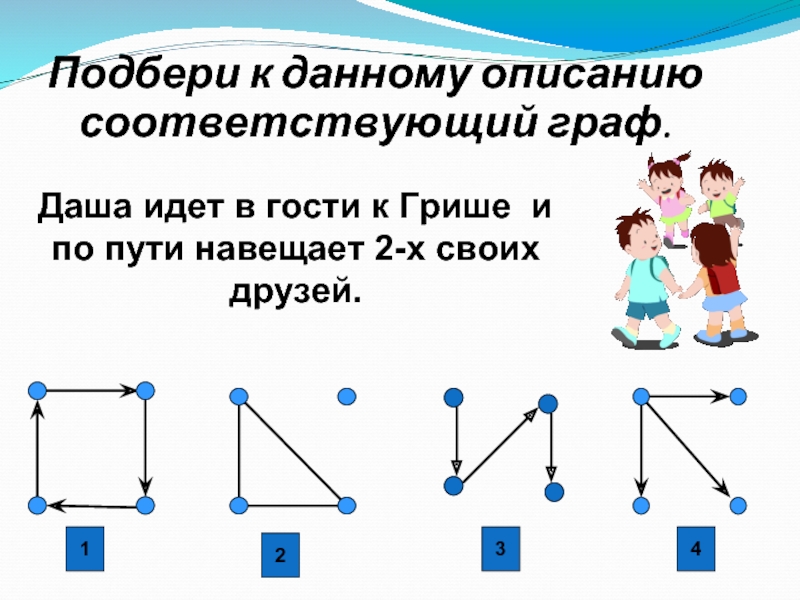
Даша идет в гости к Грише и по пути навещает
2-х своих друзей.
Подбери к данному описанию
соответствующий граф.
1
2
3
4
Слайд 32
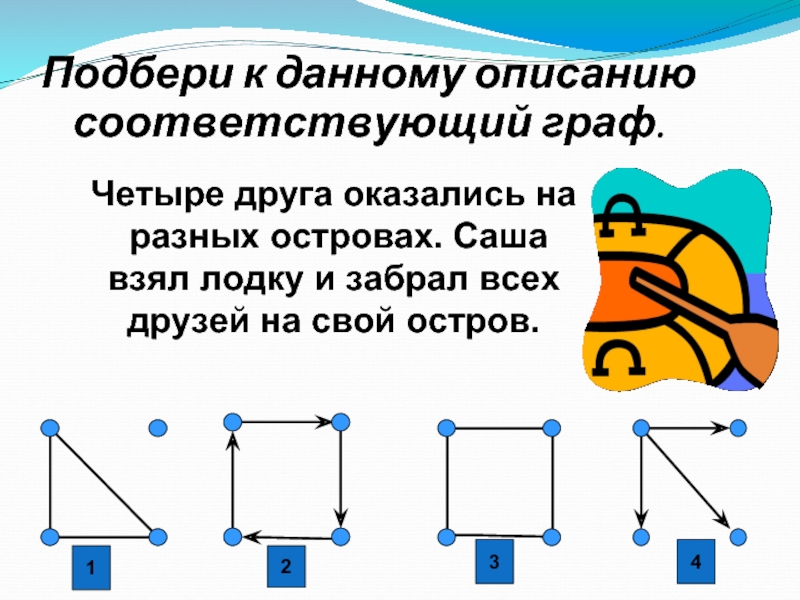
Подбери к данному описанию
соответствующий граф.
Четыре друга оказались на
разных
островах. Саша
взял лодку и забрал всех
друзей на свой
остров.2
3
4
1
Слайд 33
Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые
ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон –
Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Слайд 34Решение
Нарисуем схему условия: планеты изобразим точками, а маршруты ракет –
линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Слайд 35
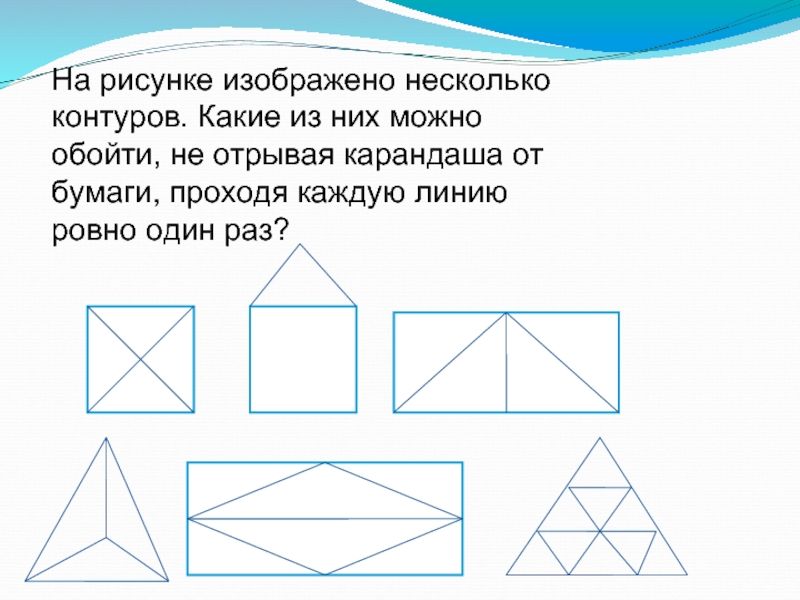
На рисунке изображено несколько контуров. Какие из них можно обойти,
не отрывая карандаша от бумаги, проходя каждую линию ровно один
раз?
Слайд 36Выводы
Графы – это замечательные математические объекты, с помощью которых можно
решать математические, экономические и логические задачи. Также можно решать различные
головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используются при составлении карт и генеалогических древ.В математике даже есть специальный раздел, который так и называется: «Теория графов».
содержание
Теги
