Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод мажорант
Содержание
- 1. Метод мажорант
- 2. «majorer» - объявлять большим«minorer» - объявлять меньшим.Название метода мажорант происходит от французских слов
- 3. Мажорантой данной функции f(х) на множестве Р,
- 4. Примеры функций, имеющих мажорантуМММММ=-1М=1М=М=М=0М= π
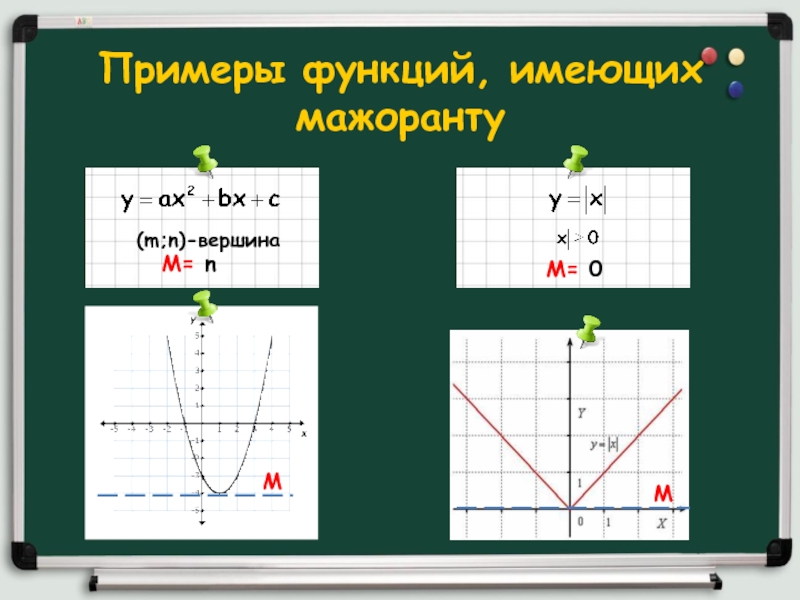
- 5. Примеры функций, имеющих мажорантуММ(m;n)-вершинаМ= nМ= 0
- 6. Оценить левую часть: f(x) Оценить правую часть:
- 7. Решить уравнение:Решение:ОДЗ: 4-х ≥ 0,
- 8. +-23max3- внутренняя точка области определения =˃ 3
- 9. Решение первого уравнения системы: х=3- входит в
- 10. Решить уравнение:Решение:Оценим правую часть уравнения:Оценим левую часть уравнения:C одной стороныс другой стороныУравнениеимеет решение, если
- 11. Решение системы, а значит и уравнения: х=1.Ответ: х=1Решим первое уравнение системы:
- 12. Решить уравнение:Решение:ОДЗ: Оценим левую часть уравнения:Перемножим два неравенства:и
- 13. Оценим правую часть уравнения:Складываем двойные неравенства:Получим:C одной стороныс другой стороныУравнениеимеет решение, если
- 14. Решим второе уравнение системы:Уравнение имеет решение, если:Если:то:ухОтвет:х=2πn, n Ɛ Z
- 15. Решить неравенствоРешение:ОДЗ: х ˃ 0Преобразуем выражение: Если
- 16. C одной стороны-наибольшее значение функции,с другой стороныНеравенствоимеет
- 17. Решить неравенствоРешение:ОДЗ: Преобразуем неравенство, умножив левую и
- 18. Решим второе уравнение системыC одной стороныс другой стороныНеравенствоимеет решение, если Если то Ответ: х=3 ˃ 0
- 19. Найти все значения параметра а, при каждом
- 20. ух2-22-2
- 21. Оценим левую часть уравнения:Оценим правую часть уравнения:C
- 22. Примеры уравнений и неравенств, решаемых методом мажорант
- 23. Спасибо завнимание!
- 24. источник шаблона:Татарников Виталий Викторович учитель физики МОУ
- 25. Скачать презентанцию
«majorer» - объявлять большим«minorer» - объявлять меньшим.Название метода мажорант происходит от французских слов
Слайды и текст этой презентации
Слайд 1Метод мажорант
МБОУ «Средняя общеобразовательная школа № 77
г.Новокузнецк, Кемеровская область
Учитель математики
Федорова Татьяна Андреевна
Слайд 2 «majorer» -
объявлять большим
«minorer» -
объявлять меньшим.
Название метода мажорант происходит
от французских слов
Слайд 3Мажорантой
данной функции f(х)
на множестве Р, называется
такое число
М, что
либо f(х) ≤ М для всех х ϵ
Р,либо f(х) ≥ М для всех х ϵ Р.
Слайд 6Оценить левую часть: f(x)
Оценить правую часть: g(x)
Если f(x)≥М ,
при этом g(x)≤M ( или f(x)≤М, , при этом
g(x)≥M), составить систему уравненийf(x)=М,
g(x)= М.
Решить одно из уравнений системы
Выполнить проверку, подставив найденные корни во второе уравнение системы
Чтобы решить уравнение вида f(x)=g(x) или неравенства вида
f(x)≥ g(x), f(x)≤g(x) методом мажорант
Слайд 7Решить уравнение:
Решение:
ОДЗ: 4-х ≥ 0,
х-2
≥ 0.
Оценим правую часть уравнения:
Для этого введем функцию:
Найдем производную функции:
Найдем
критические точки: Оценим левую часть уравнения:
Слайд 8+
-
2
3
max
3- внутренняя точка области определения =˃ 3 – критическая точка
функции
4
-наибольшее значение функции
C одной стороны
с другой стороны
Уравнение имеет решение, если
Слайд 9Решение первого уравнения системы: х=3- входит в ОДЗ
Если х=3,
то
Решение системы, а значит и уравнения: х=3.
Ответ:
х=3
Слайд 10Решить уравнение:
Решение:
Оценим правую часть уравнения:
Оценим левую часть уравнения:
C одной стороны
с
другой стороны
Уравнение
имеет решение, если
Слайд 13Оценим правую часть уравнения:
Складываем двойные неравенства:
Получим:
C одной стороны
с другой стороны
Уравнение
имеет
решение, если
Слайд 15Решить неравенство
Решение:
ОДЗ: х ˃ 0
Преобразуем выражение:
Если х ˃0, то
,тогда
для любых х из ОДЗ
Оценим левую часть неравенства:
Для этого введем
функцию:Найдем производную функции:
Найдем критические точки:
+
-
0
1
max
Слайд 16C одной стороны
-наибольшее значение функции
,с другой стороны
Неравенство
имеет решение, если
Решение
системы, а значит и неравенства: х=1.
Ответ:
х=1
при х=1-входит в ОДЗ.
Слайд 17Решить неравенство
Решение:
ОДЗ:
Преобразуем неравенство, умножив левую и правую части на
,то
Оценим
левую часть неравенства:
˃ 0
Т.к.
˃ 0
Оценим правую часть неравенства:
Слайд 18Решим второе уравнение системы
C одной стороны
с другой стороны
Неравенство
имеет решение, если
Если
то
Ответ:
х=3
˃ 0
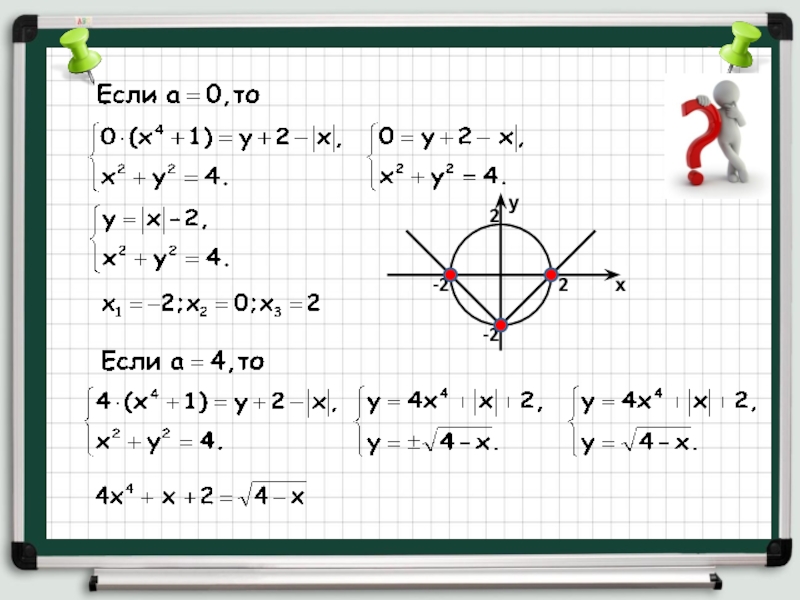
Слайд 19Найти все значения параметра а, при каждом из которых система
имеет единственное решение:
Решение:
Заметим, что в силу симметричности корней, если пара
(х;у) является решением системы, то и пара (-х;у) тоже решение системы. Единственность решения возможно только, если х=0.
Слайд 21Оценим левую часть уравнения:
Оценим правую часть уравнения:
C одной стороны
с другой
стороны
Уравнение
имеет решение, если
Решим второе уравнение системы:
Ответ:
а=4
Слайд 24источник шаблона:
Татарников Виталий Викторович
учитель физики МОУ СОШ №20 п. Баранчинский,
г. Кушва, Свердловской обл.
Школьная доска
Используемые ресурсы
Картинка № 1
Картинка № 2
Картинка
№ 4Картинка № 3
Картинка № 5
