Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нестандартные способы решения задач на ОГЭ
Содержание
- 1. Нестандартные способы решения задач на ОГЭ
- 2. ГЕОМЕТРИЯГеометрия полна приключений, потому что за каждой
- 3. Вычисление площадей фигур на клетчатой бумаге
- 4. «Не бойтесь формул! Учитесь владеть этим инструментом
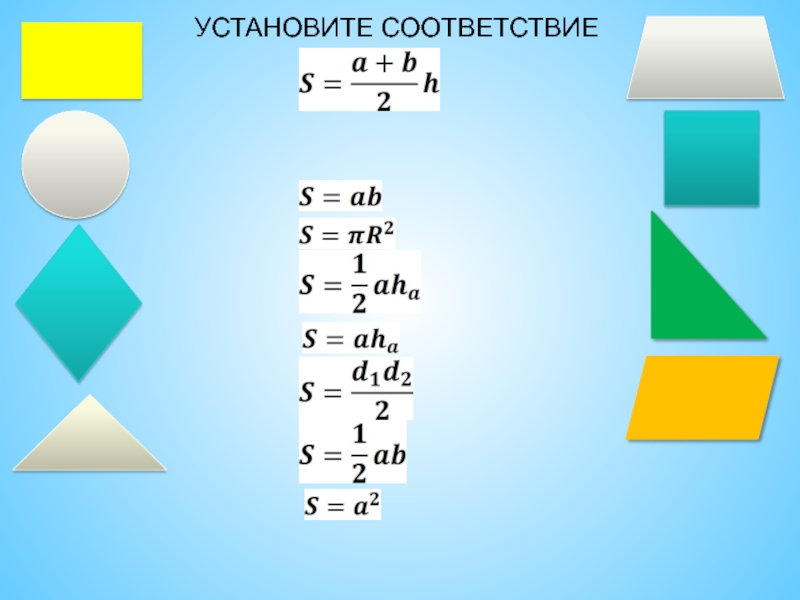
- 5. УСТАНОВИТЕ СООТВЕТСТВИЕ
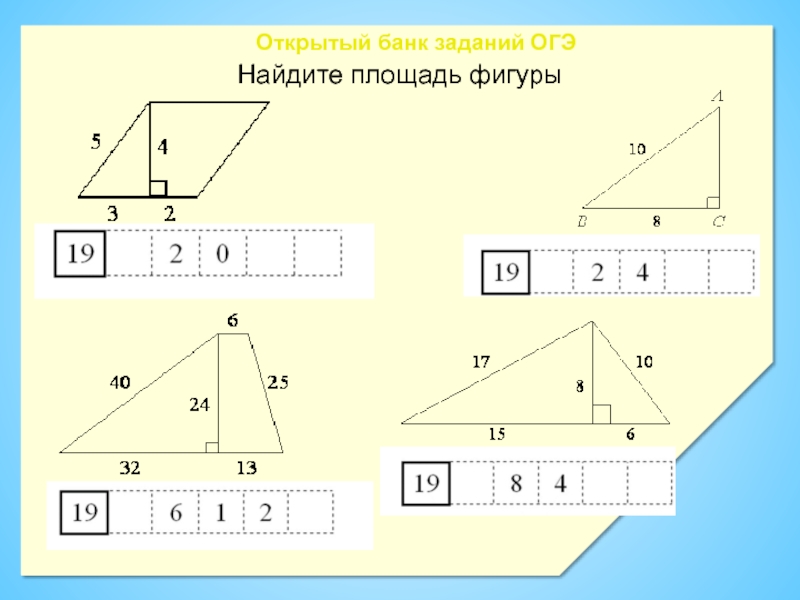
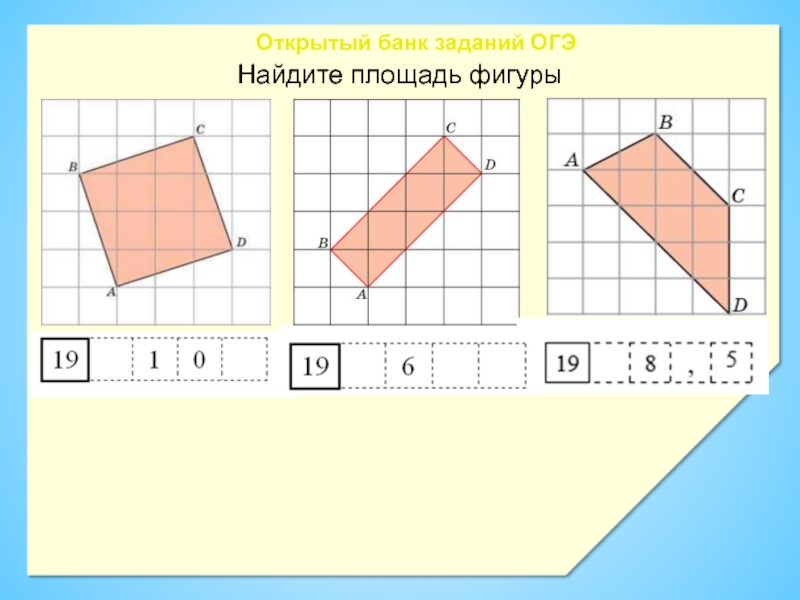
- 6. Найдите площадь фигурыОткрытый банк заданий ОГЭ
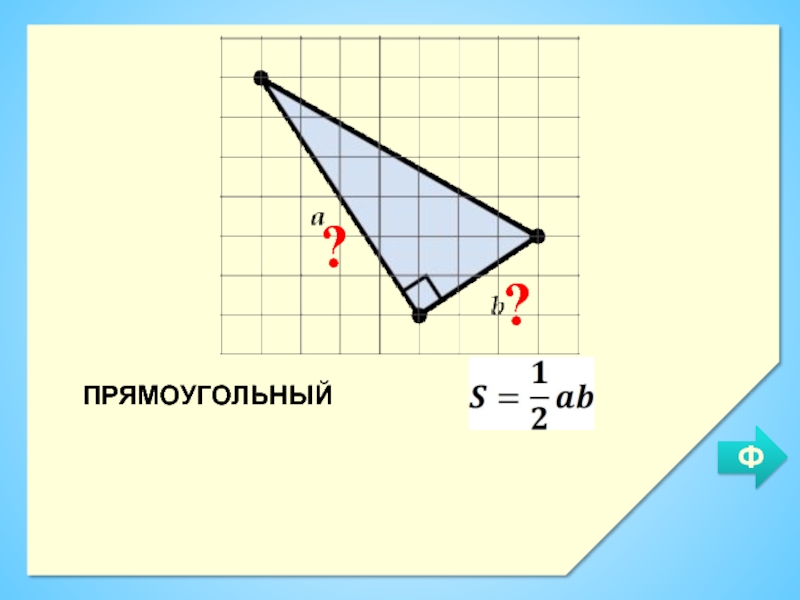
- 7. ПРЯМОУГОЛЬНЫЙ??Ф
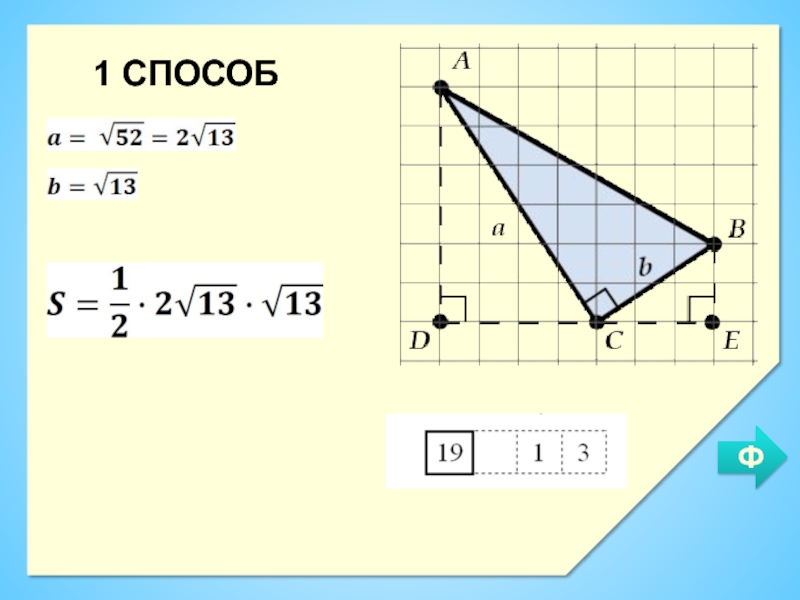
- 8. 1 СПОСОБФ
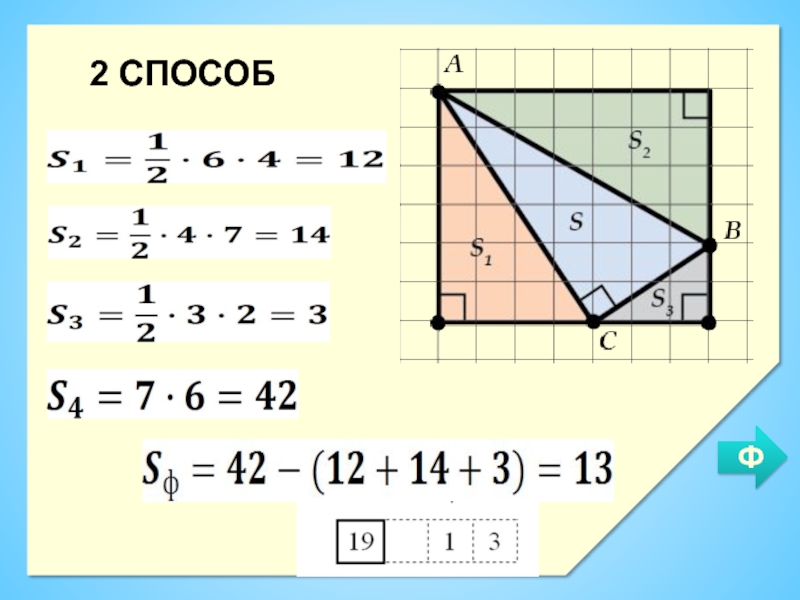
- 9. 2 СПОСОБФ
- 10. Георг ПикГеорг Александр Пик, австрийский математик (10.08.1859 — 13.07.1942)
- 11. Формула была открыта в 1899 г.Г – количество
- 12. 3 СПОСОБФОРМУЛА ПИКАВ — количество целочисленных точек внутри многоугольникаГ — количество целочисленных точек на границе многоугольникаФ
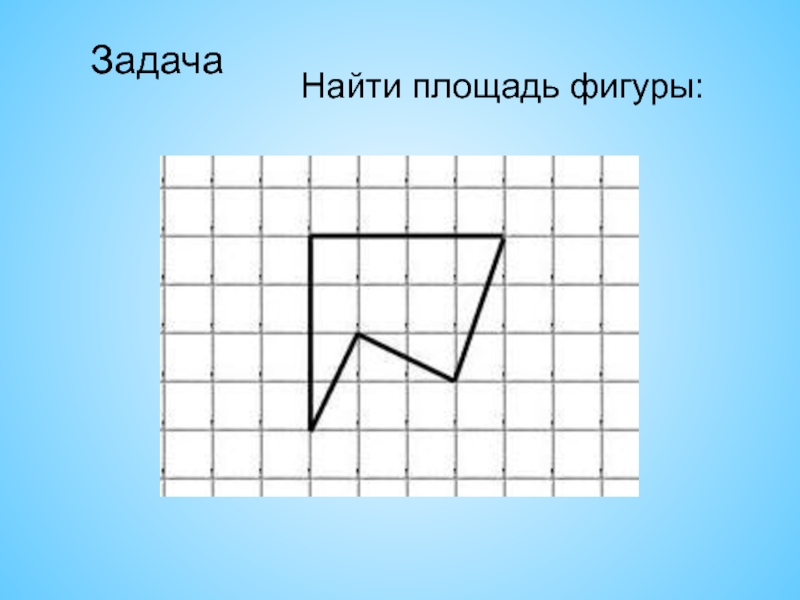
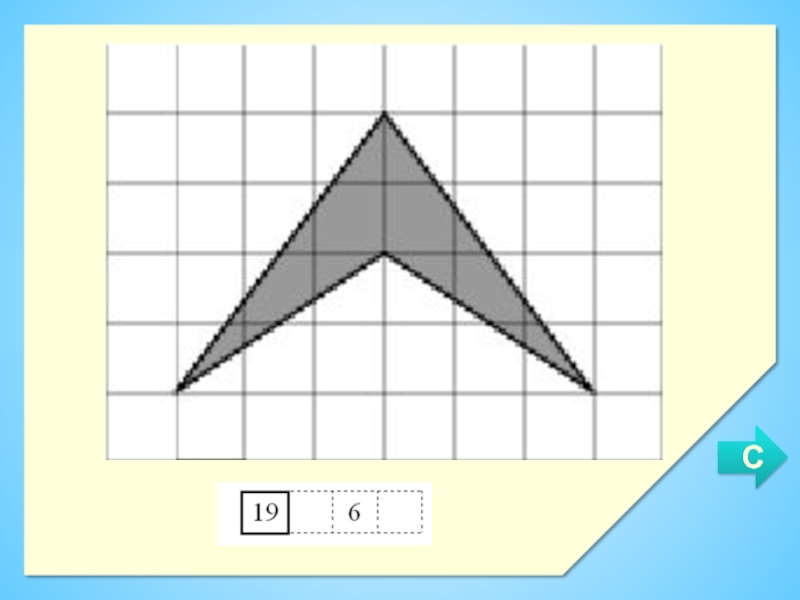
- 13. ЗадачаНайти площадь фигуры:
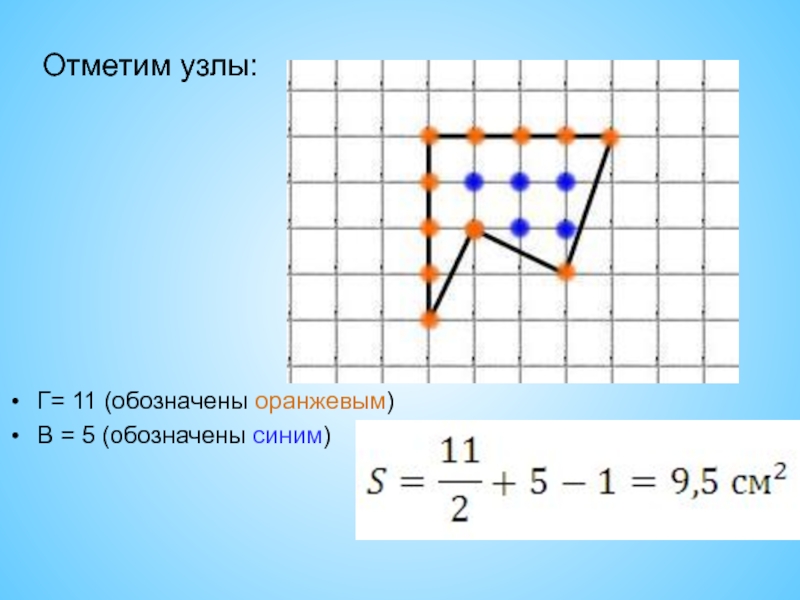
- 14. Г= 11 (обозначены оранжевым)В = 5 (обозначены синим)Отметим узлы:
- 15. С
- 16. Найдите площадь фигурыОткрытый банк заданий ОГЭ
- 17. На клетчатой бумаге с размером клетки 1×1
- 18. Слайд 18
- 19. Найдите площадь четырехугольника, изображенного на
- 20. АлгебраРешение задач на смеси и сплавы
- 21. Задачи на «концентрацию», на «смеси и
- 22. Возьмем 180 грамм воды и
- 23. Покажем этот раствор в виде прямоугольника
- 24. Возьмем 15 кг цемента и 45 кг
- 25. Покажем эту смесь в виде прямоугольника
- 26. Задача №1Имеется 30 кг 26% го раствора
- 27. Слайд 27
- 28. Задача №2Из чаши, содержащей 300 граммов 6%
- 29. Нарисуйте и заполните рисунок
- 30. Проверим!
- 31. Смешав 30-процентный и 60-процентный растворы кислоты и
- 32. Метод Пирсонапри решении задач на смеси и сплавы
- 33. Теоретические основырешения задач «на смеси, сплавы» Примем некоторые
- 34. Готовим раствор определенной концентрации. Имеется 2 раствора
- 35. При решении задач на растворы с разными
- 36. Задача 3. Морская вода содержит 5%
- 37. Задача 4. Из сосуда, доверху наполненного 97%
- 38. Задача 5 . Смешали 500 г 10%-го
- 39. Задача 6. Имеются два слитка, содержащие медь.
- 40. Задача 7. Сплавили 300 г сплава олова
- 41. Задача 8. В сосуд, содержащий 5 литров
- 42. Реши сам!1) Смешали 3 литра 25-процентного водного
- 43. Математика-наука интересная, сложная,поэтому нельзя упускать ни одной возможности сделать её более доступной!
- 44. Спасибо за внимание
- 45. Если вы хотите научиться плавать, то
- 46. Скачать презентанцию
ГЕОМЕТРИЯГеометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов)
Слайды и текст этой презентации
Слайд 1
Нестандартные способы решения задач на ОГЭ
Подготовила:
Князева Ольга Юрьевна
учитель математики
Слайд 2ГЕОМЕТРИЯ
Геометрия полна приключений, потому что за каждой задачей скрывается приключение
мысли. Решить задачу – это значит пережить приключение.
(В. Произволов)
Слайд 4«Не бойтесь формул! Учитесь владеть этим инструментом человеческого гения! В
формулах заключено величие и могущество разума…» Марков А. А.
Слайд 11Формула была открыта в 1899 г.
Г – количество узлов на границе
треугольника (на сторонах и вершинах):
В – количество узлов внутри треугольника;
*
Под «узлами» имеется ввиду пересечение линий.Площадь искомой фигуры можно найти по формуле:
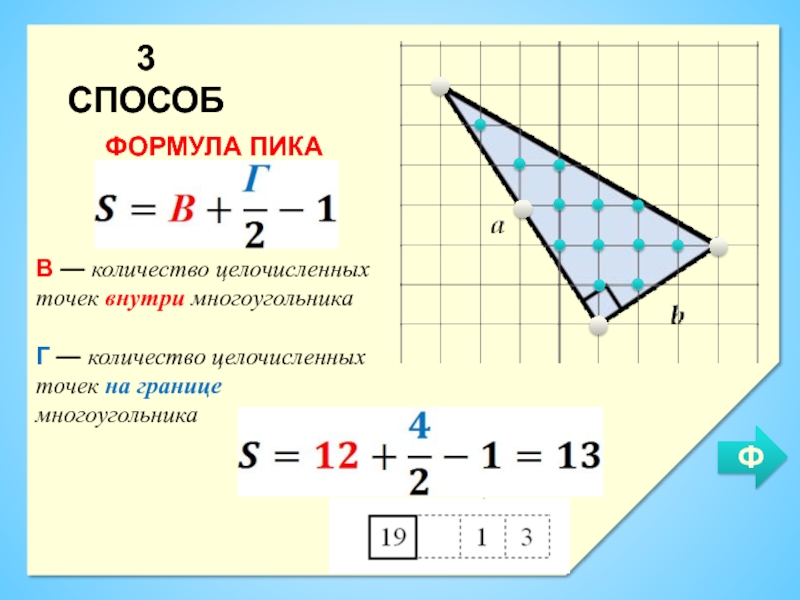
Слайд 123 СПОСОБ
ФОРМУЛА ПИКА
В — количество целочисленных точек внутри многоугольника
Г — количество
целочисленных точек на границе многоугольника
Ф
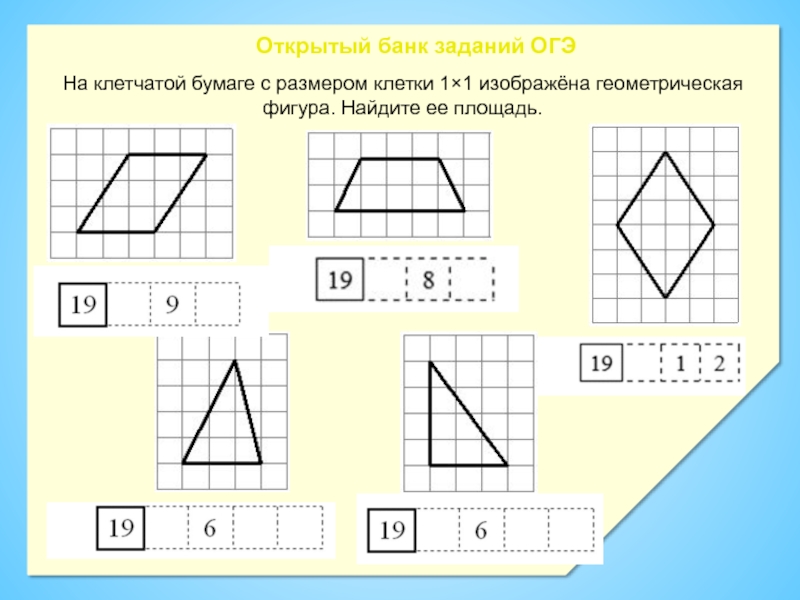
Слайд 17На клетчатой бумаге с размером клетки 1×1 изображёна геометрическая фигура.
Найдите ее площадь.
Открытый банк заданий ОГЭ
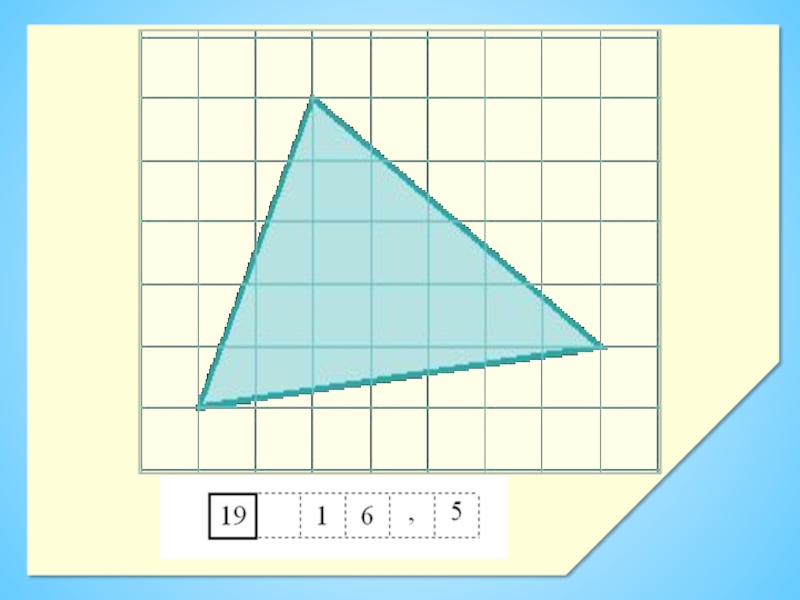
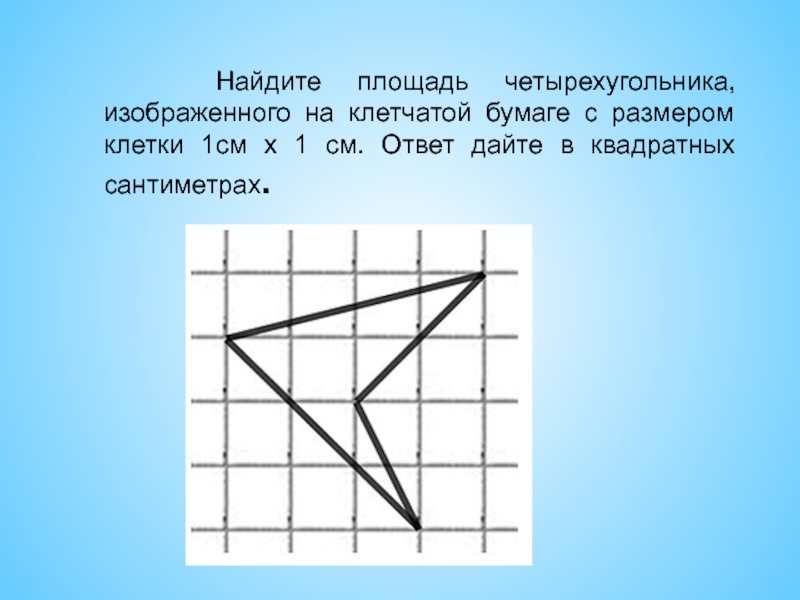
Слайд 19 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с
размером клетки 1см х 1 см. Ответ дайте в квадратных
сантиметрах.
Слайд 21Задачи на «концентрацию»,
на «смеси и сплавы»
-концентрация(доля чистого вещества в
смеси)
-количество чистого вещества в смеси
-масса смеси.
масса смеси х концентрация
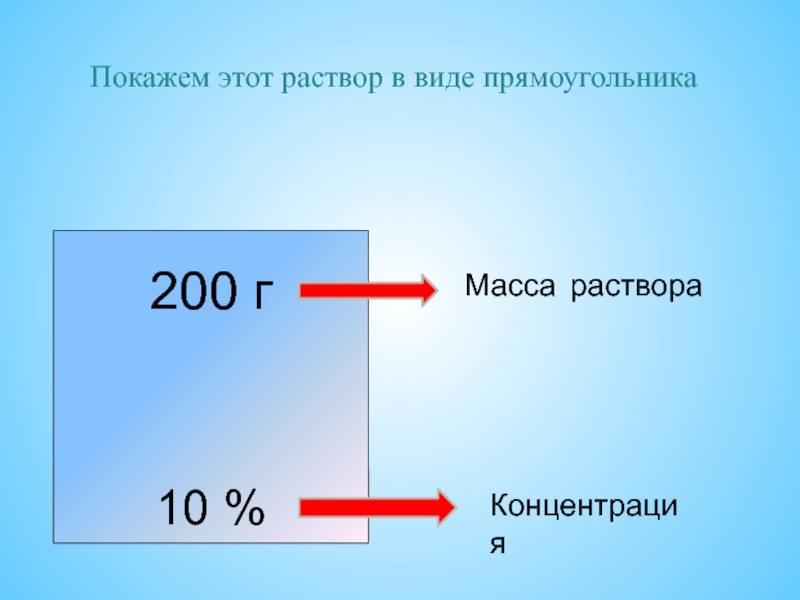
= количество чистого вещества.
Слайд 22 Возьмем 180 грамм воды и добавим в воду 20 грамм
соли. Получим раствор соли, его масса равна 180 + 20
= 200 грамм.Концентрация соли
(процентное содержание
соли) - это отношение количества
соли к количеству раствора,
записанное в процентах -
(20 : 200) ·100 = 10%
Слайд 24Возьмем 15 кг цемента и 45 кг песка, высыпим содержимое
ведер в ящик и тщательно перемешаем цемент с песком. Получим
смесь цемента с песком, её масса равна 15 кг + 45 кг = 60 кг.Концентрация цемента
(процентное содержание
цемента) – это
отношение количества
цемента к количеству
смеси, записанное
в процентах –
(15 : 60) ·100 = 25%
Слайд 26Задача №1
Имеется 30 кг 26% го раствора соли. Требуется получить
40% раствор соли. Сколько кг 50% раствора соли нужно добавить?
30 кг
26 %
50 %
40 %
Имеется
Нужно добавить
Требуется получить
=
+
х кг
(30+х )кг
Слайд 28Задача №2
Из чаши, содержащей 300 граммов 6% раствора уксусной кислоты,
отлили некоторое количество этого раствора и добавили такое же количество
воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты
Слайд 30Проверим!
300 г
6%
Было
Отлили
Добавили
Получили
х г
6%
х г
0%
300 г
2%
-
=
+
300 · 6 – 6х + х·0 = 300 · 2
Ответ: 200 г.
Слайд 31Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг
чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10
кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?Решение:
Х
30%
У
60%
10
0%
Х+у+10
36%
Х+у+10
41%
10
50%
У
60%
Х
30%
Составим систему уравнений:
30х+60у+10*0=(х+у+10)*36,
30х+60у+10*50=(х+у+10)*41.
Решая ее, получаем х=60, у=30.
Ответ: 60.
Слайд 33Теоретические основы
решения задач «на смеси, сплавы»
Примем некоторые допущения:
Все получающиеся сплавы
или смеси однородны.
При решении этих задач считается, что масса смеси
нескольких веществ равна сумме масс компонентов.Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.
Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества. Всё это синонимы.
Слайд 34Готовим раствор определенной концентрации. Имеется 2 раствора с более высокой
и менее высокой концентрацией, чем нужно.
Обозначим массу 1-го раствора m
1, а 2-го m 2, тогда при смешивании масса смеси будет равна сумме этих масс.
Массовая доля растворённого вещества в 1-м растворе – q 1, во 2-м – q 2, а в их смеси – q 3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: m 1 q 1 + m 2q2 =q3(m 1 + m 2),
m 1(q 1 – q 3) = m 2(q 3 – q2) Отношение массы 1-го раствора к массе 2-го раствора это отношение разности массовых долей растворённого вещ-ва в смеси и в 2-м растворе к разности величин в 1-м растворе и в смеси.
Слайд 35
При решении задач на растворы с разными концентрациями чаще всего
применяют квадрат Пирсона.
При расчётах записывают одну над другой массовые доли
растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
q1 q3 — q2
q3
q2 q1 — q3
Слайд 36Задача 3. Морская вода содержит 5% соли (по массе). Сколько
пресной воды нужно добавить к 30 кг морской воды, чтобы
концентрация соли составила 1,5%?Решение:
Слайд 37Задача 4. Из сосуда, доверху наполненного 97% раствором кислоты, отлили
2 литра жидкости и долили 2 литра 45% раствора этой
же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд?Решение:
97%
81%
45%
Слайд 38Задача 5 .
Смешали 500 г 10%-го раствора соли и
400 г 55%-го раствора соли. Определите концентрацию соли в смеси.
Решение:
Слайд 39Задача 6. Имеются два слитка, содержащие медь. Масса второго слитка
на 3 кг больше, чем масса первого слитка. Процентное содержание
меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка.Решение:
Слайд 40Задача 7. Сплавили 300 г сплава олова и меди, содержащего
60% олова, и 900г сплава олова и меди, содержащего 80%
олова. Сколько процентов олова в получившемся сплаве?Решение:
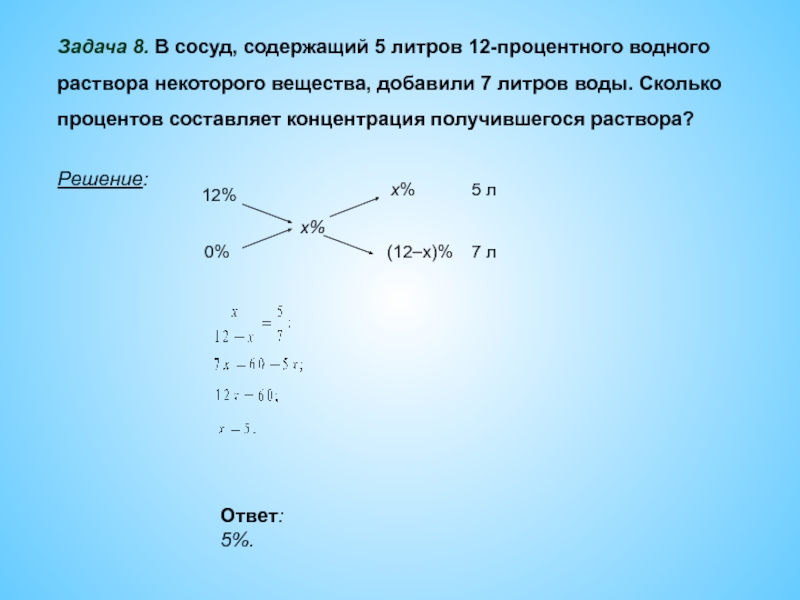
Слайд 41Задача 8. В сосуд, содержащий 5 литров 12-процентного водного
раствора некоторого
вещества, добавили 7 литров воды. Сколько
процентов составляет концентрация получившегося раствора?
Решение:
Ответ:
5%.
Слайд 42Реши сам!
1) Смешали 3 литра 25-процентного водного раствора некоторого вещества
с 12 литрами 15-процентного водного раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?2) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
3) Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава.
4) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
Слайд 43Математика-наука интересная, сложная,
поэтому нельзя упускать ни одной возможности
сделать её
более доступной!
Слайд 45Если вы хотите научиться плавать,
то смело входите в
воду, а если хотите научиться решать задачи,
то решайте их!
