Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пробный ОГЭ по математике 2017
Содержание
- 1. Пробный ОГЭ по математике 2017
- 2. Цель:Рассмотреть задания, которые были на пробном ОГЭ;Сделать анализ допущенных ошибок;Провести коррекцию знаний учащихся
- 3. Найти значение выражения(№1)3,5⋅6,6+1,63.4,1⋅7,7+0,86.− 3,41+8,4⋅1,4− 2,07+5,3⋅6,6.24,7332,438,3532,91
- 4. Задание №2На координатной прямой отмечены числа а
- 5. Найти значение выражения №34896126198
- 6. Найти корень уравнения(№4)-18-20144,2
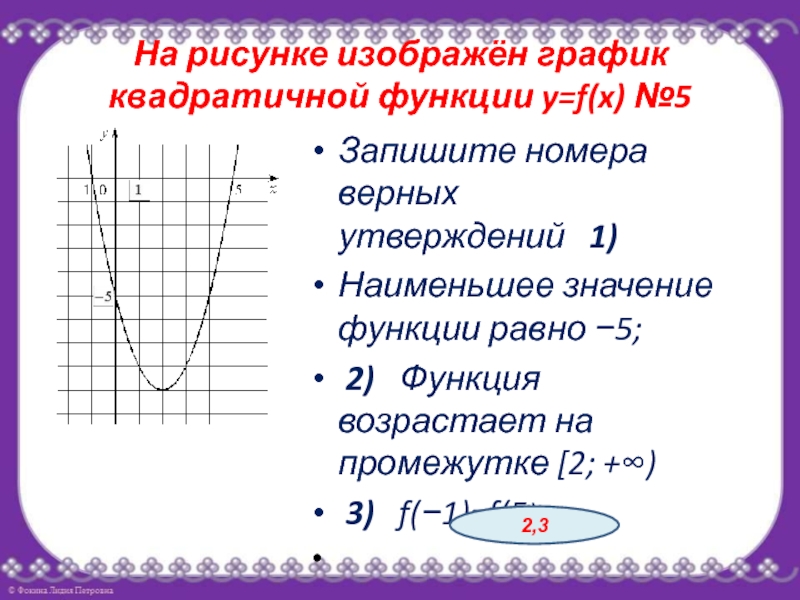
- 7. На рисунке изображён график квадратичной функции y=f(x) №5Запишите
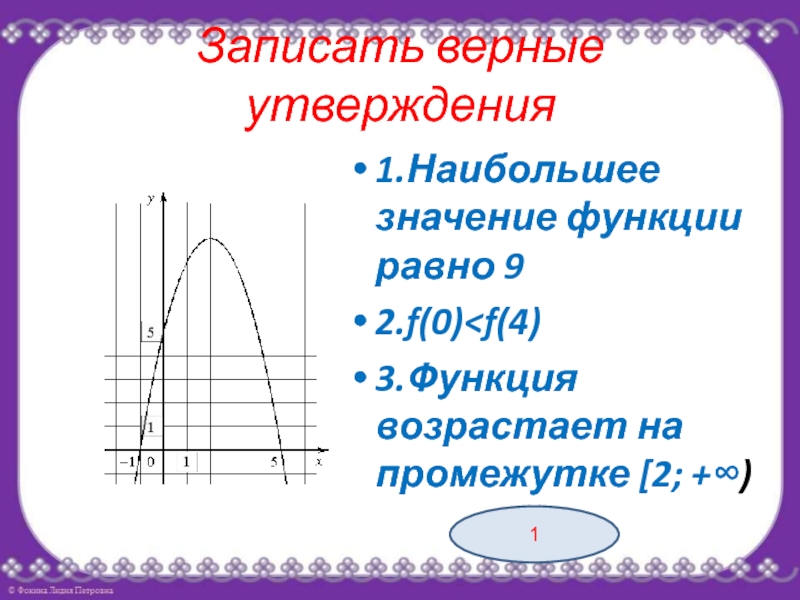
- 8. Записать верные утверждения1.Наибольшее значение функции равно 92.f(0)
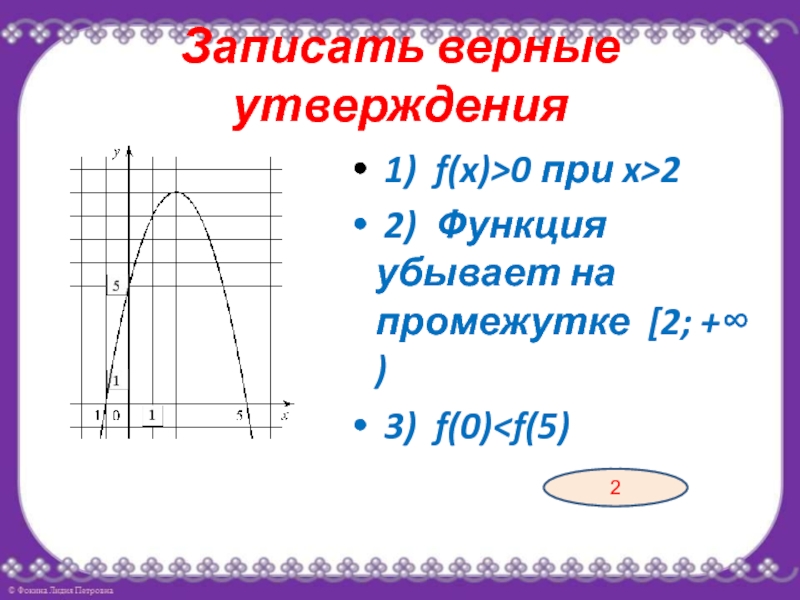
- 9. Записать верные утверждения 1) f(x)>0 при x>2 2) Функция убывает на промежутке [2; +∞) 3) f(0)
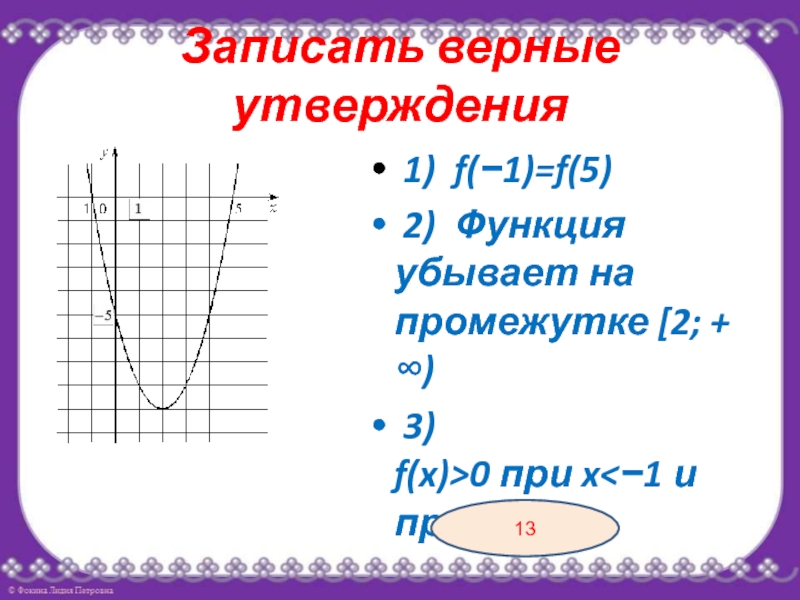
- 10. Записать верные утверждения 1) f(−1)=f(5) 2) Функция убывает на промежутке [2; +∞) 3) f(x)>0 при x513
- 11. №61) Выписаны первые несколько членов арифметической прогрессии:30;
- 12. Задание №70,750,6
- 13. №81)Укажите решение неравенства 4x−4 ≥ 9x+6 1)[− 0,4 ; +∞);
- 14. Блок «Геометрия»1)№9.Найдите больший угол равнобедренной трапеции ABCD,
- 15. 3)Найдите меньший угол равнобедренной трапеции ABCD,
- 16. №10Точка O – центр окружности, на которой лежат точки
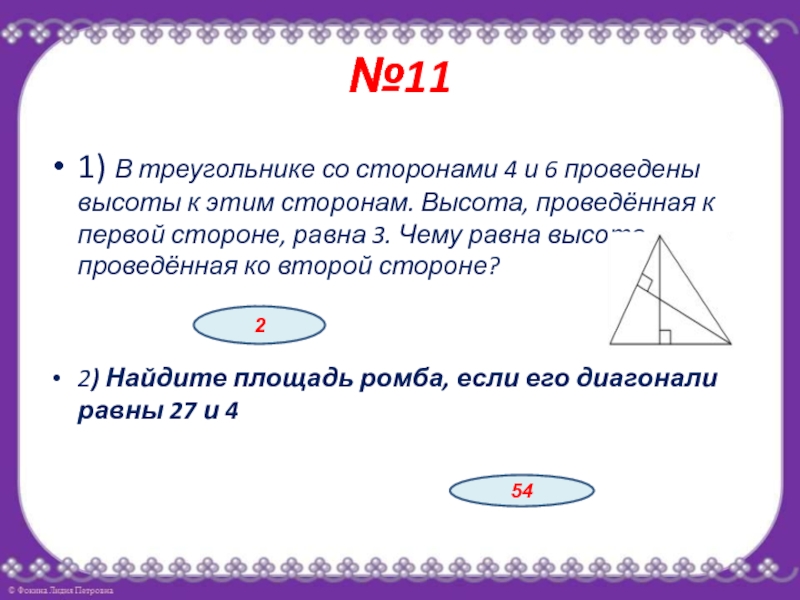
- 17. №111) В треугольнике со сторонами 4 и
- 18. 3) В треугольнике со сторонами 6 и
- 19. №121) Катеты прямоугольного треугольника равны
- 20. Какое из следующих утверждений верно? 1) Треугольник со сторонами
- 21. 1) Две прямые, параллельные третьей прямой, перпендикулярны. 2) Треугольник со
- 22. Блок «Реальная математика»4
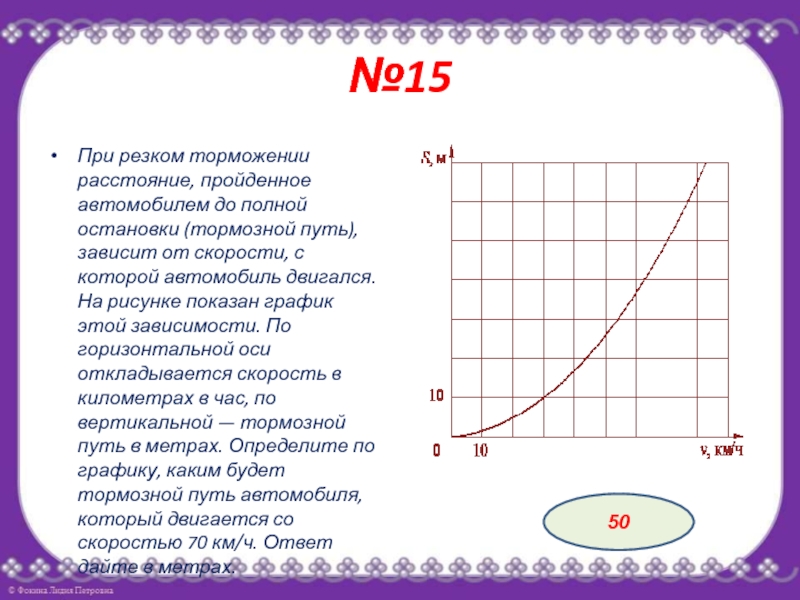
- 23. №15При резком торможении расстояние, пройденное автомобилем до
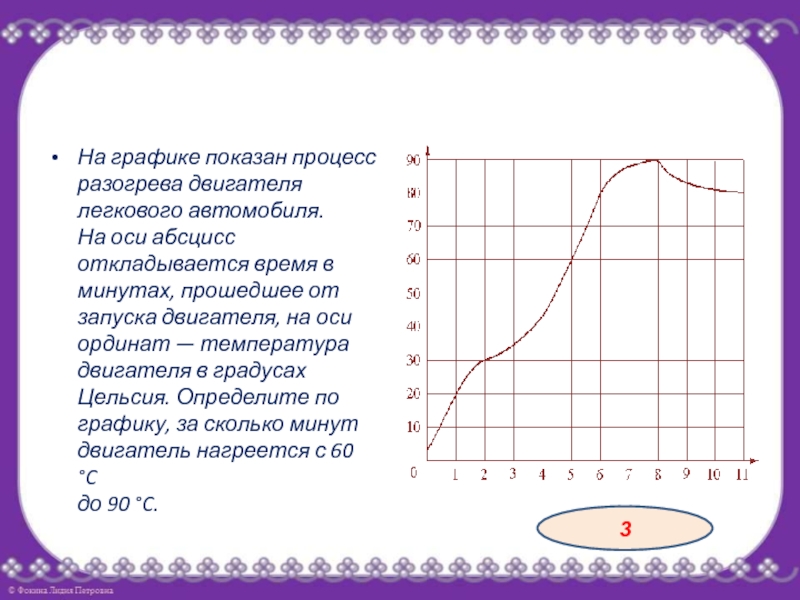
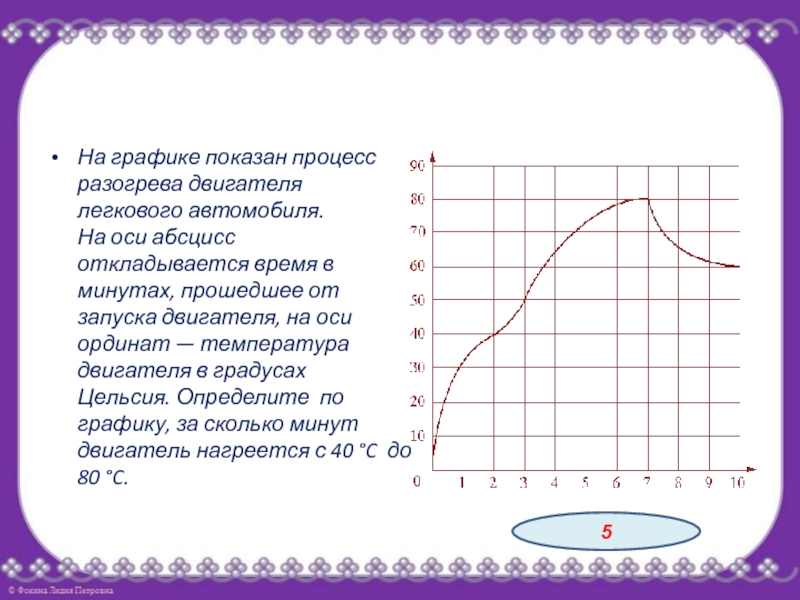
- 24. На графике показан процесс разогрева двигателя легкового
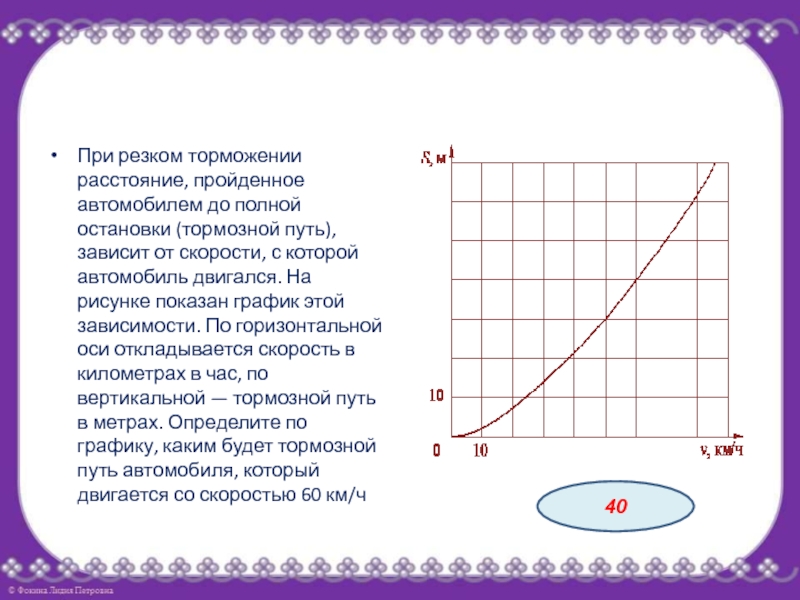
- 25. При резком торможении расстояние, пройденное автомобилем до
- 26. На графике показан процесс разогрева двигателя легкового
- 27. №161) В городе 55 000 жителей, причём
- 28. №163) В городе 90000 жителей, причём 17%
- 29. №171)Две трубы, диаметры которых равны 30 см
- 30. 3) Две трубы, диаметры которых равны 24
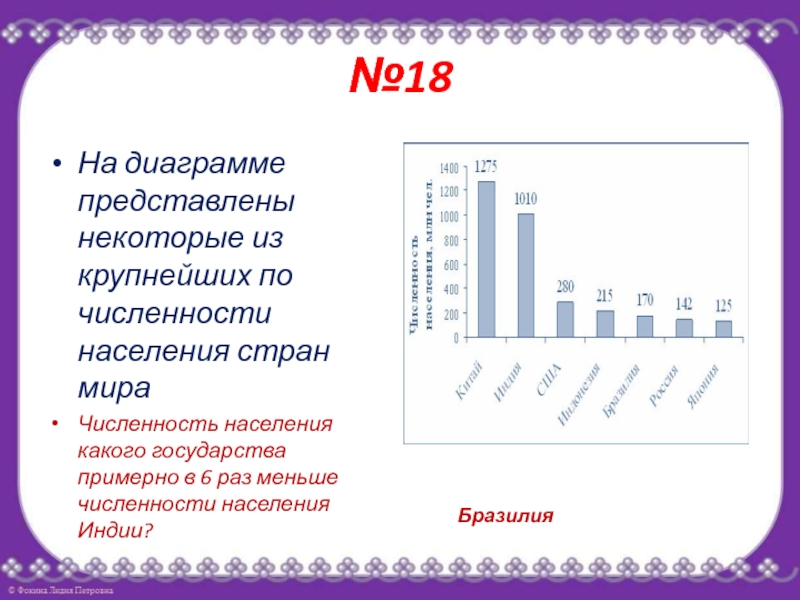
- 31. №18На диаграмме представлены некоторые из крупнейших по
- 32. №18На диаграмме представлены некоторые из крупнейших по
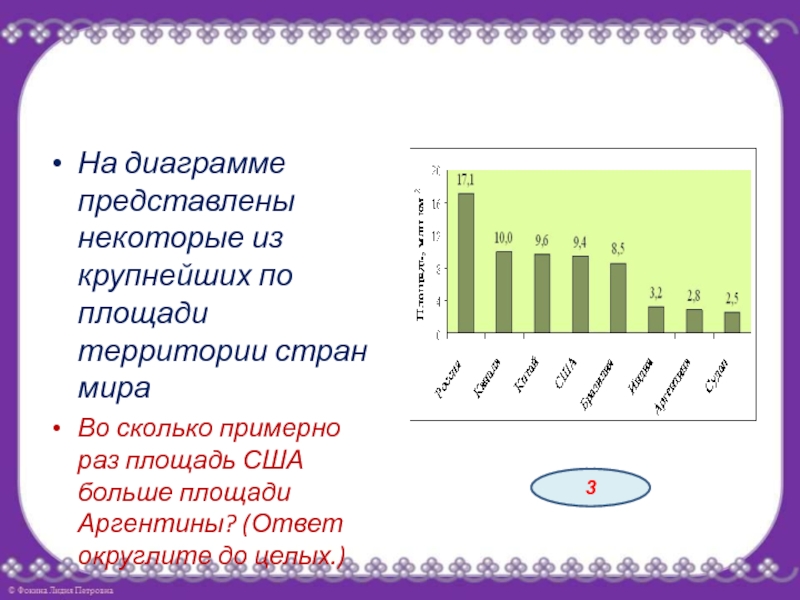
- 33. На диаграмме представлены некоторые из крупнейших по
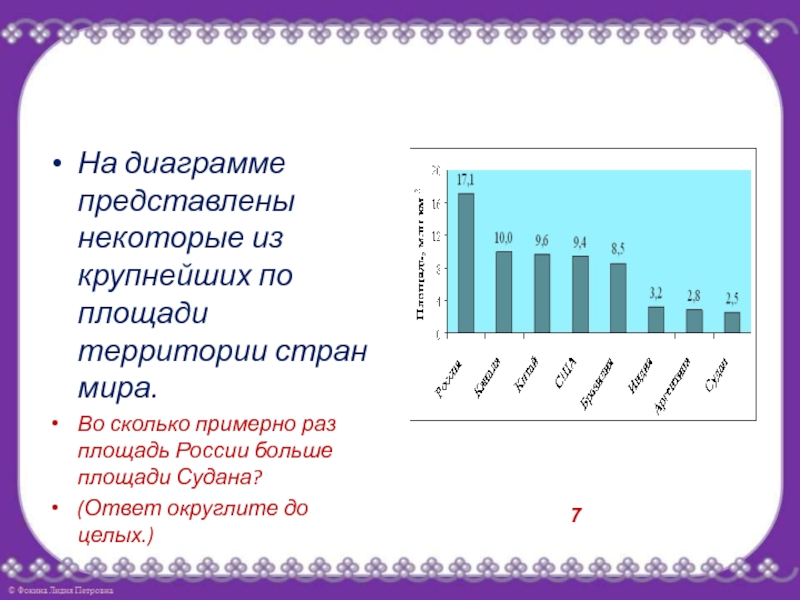
- 34. На диаграмме представлены некоторые из крупнейших по
- 35. №19Расстояние от Солнца до Юпитера равно 779 000 000
- 36. №20Закон Менделеева–Клапейрона можно записать в виде PV=νRT,
- 37. 2)Закон Менделеева–Клапейрона можно записать в виде PV=νRT,
- 38. Удачи вам, ребята!
- 39. Информационные источникиhttp://img-fotki.yandex.ru/get/9501/16969765.224/0_8ebf8_55886329_L.png бордюр
- 40. Скачать презентанцию
Цель:Рассмотреть задания, которые были на пробном ОГЭ;Сделать анализ допущенных ошибок;Провести коррекцию знаний учащихся
Слайды и текст этой презентации
Слайд 2Цель:
Рассмотреть задания, которые были на пробном ОГЭ;
Сделать анализ допущенных ошибок;
Провести
коррекцию знаний учащихся
Слайд 3Найти значение выражения(№1)
3,5⋅6,6+1,63.
4,1⋅7,7+0,86.
− 3,41+8,4⋅1,4
− 2,07+5,3⋅6,6.
24,73
32,43
8,35
32,91
Слайд 4Задание №2
На координатной прямой отмечены числа а и b.
Какое из
следующих утверждений неверно:
1)а + b < 0; 2) – 4
< a – 1 < – 3 3)a2b < 0; 4) – b < 0
4
Слайд 7На рисунке изображён график квадратичной функции y=f(x) №5
Запишите номера верных утверждений
1)
Наименьшее значение функции равно −5;
2) Функция возрастает на промежутке [2; +∞)
3) f(−1)=f(5)
2,3
Слайд 9Записать верные утверждения
1) f(x)>0 при x>2
2) Функция убывает на промежутке [2; +∞)
3) f(0)
Слайд 10Записать верные утверждения
1) f(−1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x5
13
Слайд 11№6
1) Выписаны первые несколько членов арифметической прогрессии:
30; 27; 24; …
Найдите 5-й член этой прогрессии
2) Выписаны первые несколько членов арифметической
прогрессии: 2; 6; 10; … Найдите её шестнадцатый член.
18
62
Слайд 13№8
1)Укажите решение неравенства
4x−4 ≥ 9x+6
1)[− 0,4 ; +∞); 2) (− ∞ ; −2]
; 3)[− 2 ; +∞); 4)(− ∞ ; −0,4]
2) Укажите решение неравенства 5x+4≤x+6.
1)(− ∞ ; 0,5]; 2) (− ∞ ; 2,5]; 3)[0,5 ; +∞);
4)[2,5 ; +∞)2
1
![№81)Укажите решение неравенства 4x−4 ≥ 9x+6 1)[− 0,4 ; +∞); 2) (− ∞ ; −2] ; 3)[− 2 ; +∞); 4)(− ∞ ; −0,4]2) Укажите решение неравенства 5x+4≤x+6.1)(− ∞ ; 0,5]; 2)](/img/thumbs/dbf7df1b196bd715f7678bd27a42ca07-800x.jpg "Пробный ОГЭ по математике 2017 №81)Укажите решение неравенства 4x−4 ≥ 9x+6 1)[− 0,4 ; +∞); 2) (− ∞ ; −2] ; 3)[− 2 ; +∞);")
Слайд 14Блок «Геометрия»
1)№9.Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС
образует с основанием AD и боковой стороной АВ углы, равные
25° и 40° соответственно.115
2) Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
110
Слайд 15
3)Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС
образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно. Ответ дайте в градусах.55
4) Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 25° и 110°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
45
Слайд 16№10
Точка O – центр окружности, на которой лежат точки E, F и G таким
образом, что OEFG – ромб. Найдите угол EFG. Ответ дайте в градусах.
120
Слайд 17№11
1) В треугольнике со сторонами 4 и 6 проведены высоты
к этим сторонам. Высота, проведённая к первой стороне, равна 3.
Чему равна высота, проведённая ко второй стороне?2) Найдите площадь ромба, если его диагонали равны 27 и 4
2
54
Слайд 183) В треугольнике со сторонами 6 и 12 проведены высоты
к этим сторонам. Высота, проведённая к первой стороне, равна 2.
Чему равна высота, проведённая ко второй стороне?1
4) Найдите площадь ромба, если его диагонали равны 36 и 4.
72
Слайд 19№12
1) Катеты прямоугольного треугольника равны и 2. Найдите
синус наименьшего угла этого треугольника.
0,2 2) Катеты прямоугольного треугольника равны и 3. Найдите синус наименьшего угла этого треугольника.
0,2
3) Катеты прямоугольного треугольника равны и 3. Найдите синус наименьшего угла этого треугольника
0,5
Слайд 20Какое из следующих утверждений верно?
1) Треугольник со сторонами 1, 2, 4
существует.
2) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
3) Основания любой
трапеции параллельны.3
1)Боковые стороны любой трапеции равны.
2)В параллелограмме есть два равных угла.
3)Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
23
Слайд 21 1) Две прямые, параллельные третьей прямой, перпендикулярны.
2) Треугольник со сторонами 1, 2,
4 существует.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3
1) Существует прямоугольник,
диагонали которого взаимно перпендикулярны.2) Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
3) В тупоугольном треугольнике все углы тупые.
12
Слайд 23№15
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной
путь), зависит от скорости, с которой автомобиль двигался. На рисунке
показан график этой зависимости. По горизонтальной оси откладывается скорость в километрах в час, по вертикальной — тормозной путь в метрах. Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 70 км/ч. Ответ дайте в метрах.50
Слайд 24На графике показан процесс разогрева двигателя легкового автомобиля. На оси
абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на
оси ординат — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 60 °C до 90 °C.3
Слайд 25При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной
путь), зависит от скорости, с которой автомобиль двигался. На рисунке
показан график этой зависимости. По горизонтальной оси откладывается скорость в километрах в час, по вертикальной — тормозной путь в метрах. Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 60 км/ч40
Слайд 26На графике показан процесс разогрева двигателя легкового автомобиля. На оси
абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на
оси ординат — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 40 °C до 80 °C.5
Слайд 27№16
1) В городе 55 000 жителей, причём 11% — это студенты.
Сколько примерно человек составляет эта категория жителей? Ответ округлите до
тысяч.2) В городе 220000 жителей, причём 12% — это студенты. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
6
26
Слайд 28№16
3) В городе 90000 жителей, причём 17% — это дети до
14 лет. Сколько примерно человек составляет эта категория жителей? Ответ
округлите до тысяч.4) В городе 80000 жителей, причём 26% — это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
15
21
Слайд 29№17
1)Две трубы, диаметры которых равны 30 см и 40 см,
требуется заменить одной, площадь поперечного сечения которой равна сумме площадей
поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.2)Две трубы, диаметры которых равны 20 см и 21 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
50
29
Слайд 303) Две трубы, диаметры которых равны 24 см и 32
см, требуется заменить одной, площадь поперечного сечения которой равна сумме
площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.4) Две трубы, диаметры которых равны 51 см и 68 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
40
85
Слайд 31№18
На диаграмме представлены некоторые из крупнейших по численности населения стран
мира
Численность населения какого государства примерно в 6 раз меньше
численности населения Индии?Бразилия
Слайд 32№18
На диаграмме представлены некоторые из крупнейших по численности населения стран
мира.
Численность населения какого государства примерно в 6 раз меньше численности
населения Китая?ИНДОНЕЗИЯ
Слайд 33На диаграмме представлены некоторые из крупнейших по площади территории стран мира
Во
сколько примерно раз площадь США больше площади Аргентины? (Ответ округлите
до целых.)3
Слайд 34На диаграмме представлены некоторые из крупнейших по площади территории стран мира.
Во
сколько примерно раз площадь России больше площади Судана?
(Ответ округлите
до целых.)7
Слайд 35№19
Расстояние от Солнца до Юпитера равно 779 000 000 км. Сколько времени
идёт свет от Солнца до Юпитера? Скорость света равна 300 000
км/с. Ответ дайте в минутах и округлите до десятых.Расстояние от Солнца до Венеры равно
110 000 000 км. Сколько времени идёт свет от Солнца до Венеры? Скорость света равна 300000 км/с. Ответ дайте в минутах и округлите до десятых
43,3
3,2
Слайд 36№20
Закон Менделеева–Клапейрона можно записать в виде PV=νRT, где P — давление (в
паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в
градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T=700 К, P=20 941,2 Па, V=9,5 м3.34,2
Слайд 372)Закон Менделеева–Клапейрона можно записать в виде PV=νRT, где P — давление (в
паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах
Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T=400 К, P=13 296 Па, V=4,9 м3.19,6
Слайд 39Информационные источники
http://img-fotki.yandex.ru/get/9501/16969765.224/0_8ebf8_55886329_L.png бордюр
