Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки и свойства параллельных прямых
Содержание
- 1. Признаки и свойства параллельных прямых
- 2. Эпиграф к уроку: "Геометрия полна приключений, потому,что
- 3. Слайд 3
- 4. Какое название носят углы 1 и 5,
- 5. Если угол 7 равен углу 8, то
- 6. Если а ┴ с и
- 7. Через точку М, не лежащую на прямой
- 8. Через точку, не лежащую на данной прямой,
- 9. Слайд 9
- 10. АВ // СМ.
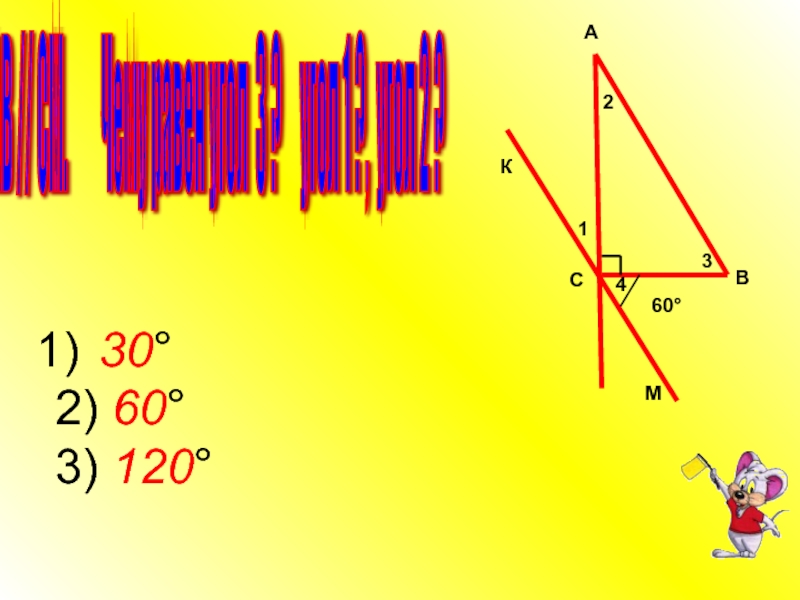
- 11. а // в Чему равен
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Евклид (III век до н. э.) Древнегреческий
- 18. «Чем отличается геометрия Лобачевского от геометрии Евклида?»
- 19. Николай Иванович Лобачевский (1792 – 1856 гг.)Все!
- 20. Слайд 20
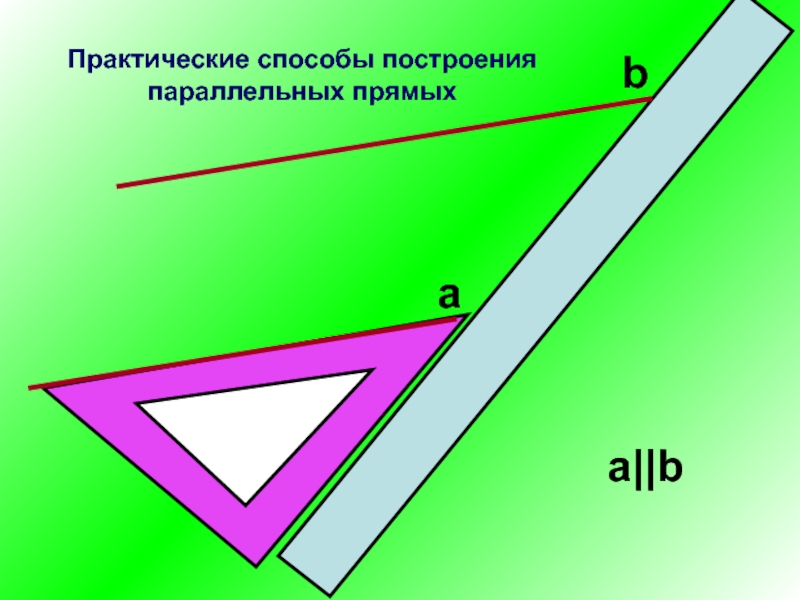
- 21. аba||bПрактические способы построения параллельных прямых
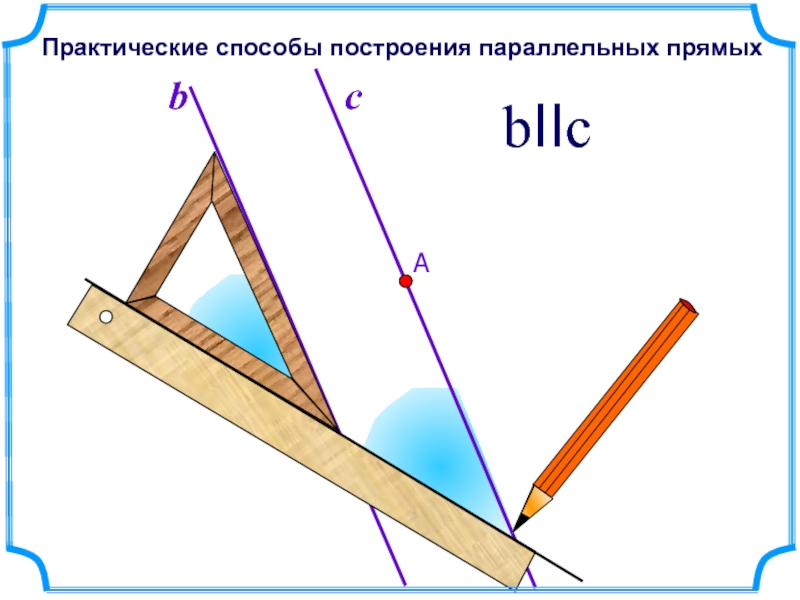
- 22. bbIIcПрактические способы построения параллельных прямых
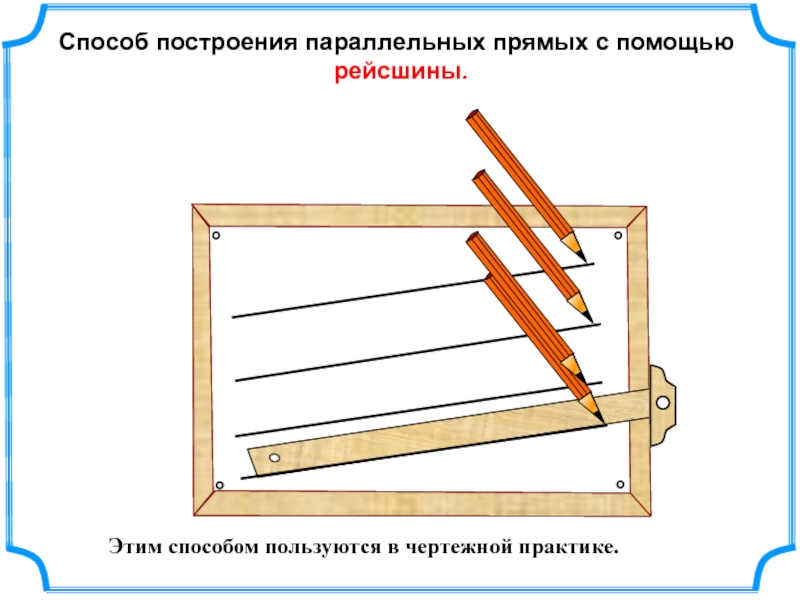
- 23. Этим способом пользуются в чертежной практике.Способ построения
- 24. Практическая работа 1)
- 25. Параллельны ли прямые а и в ? Почему ?
- 26. Параллельны ли прямые а и в ? Почему ?
- 27. Параллельны ли прямые а и в ? Почему ?
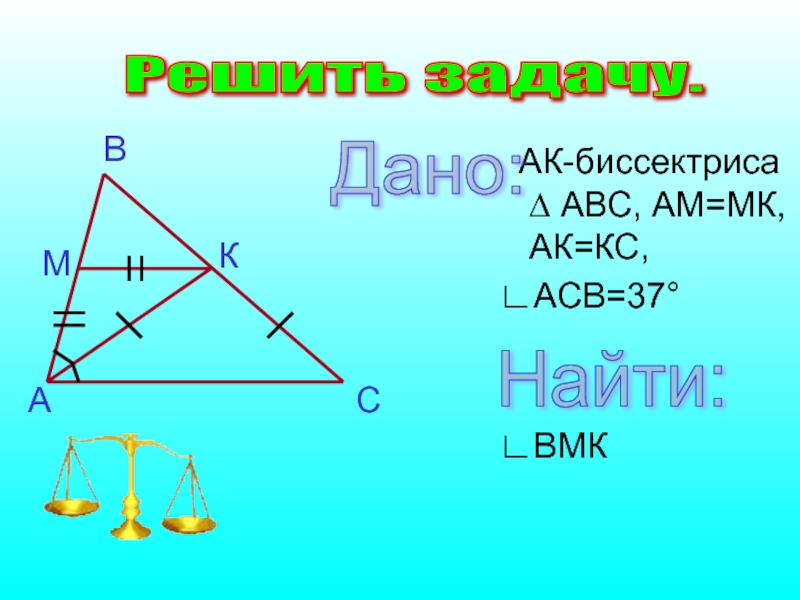
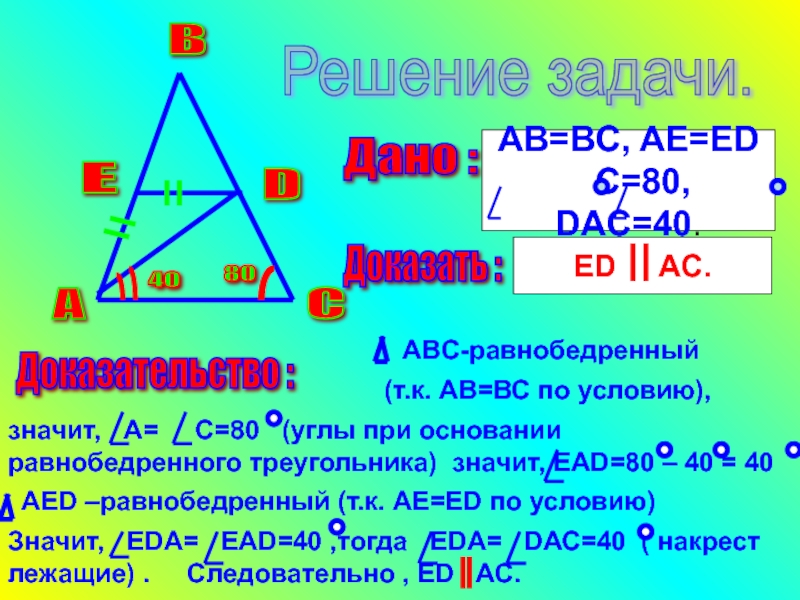
- 28. Решить задачу. АК-биссектриса ∆ АВС, АМ=МК, АК=КС,∟АСВ=37°∟ВМКДано: Найти:
- 29. Параллельные прямые
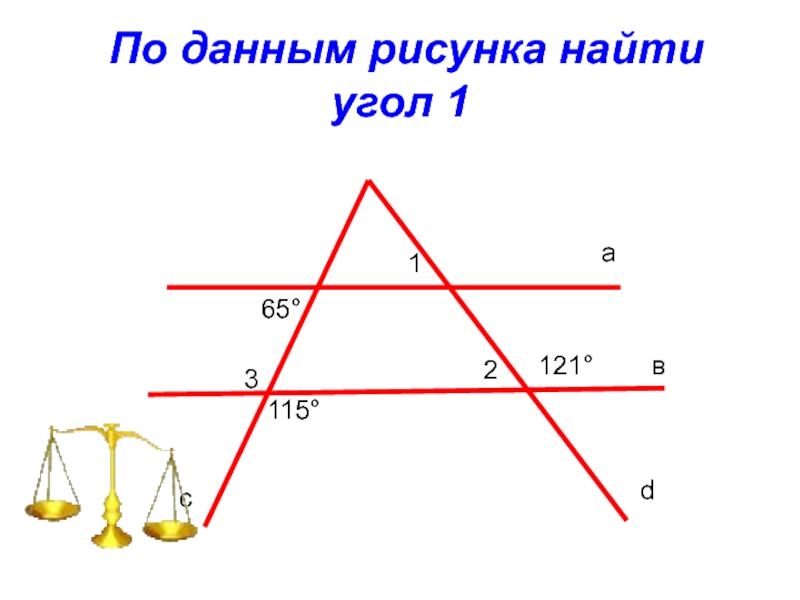
- 30. По данным рисунка найти угол 165°312121°115°авсd
- 31. Слайд 31
- 32. Решение задачи.
- 33. Самостоятельная работаВариант 1
- 34. Скачать презентанцию
Слайды и текст этой презентации
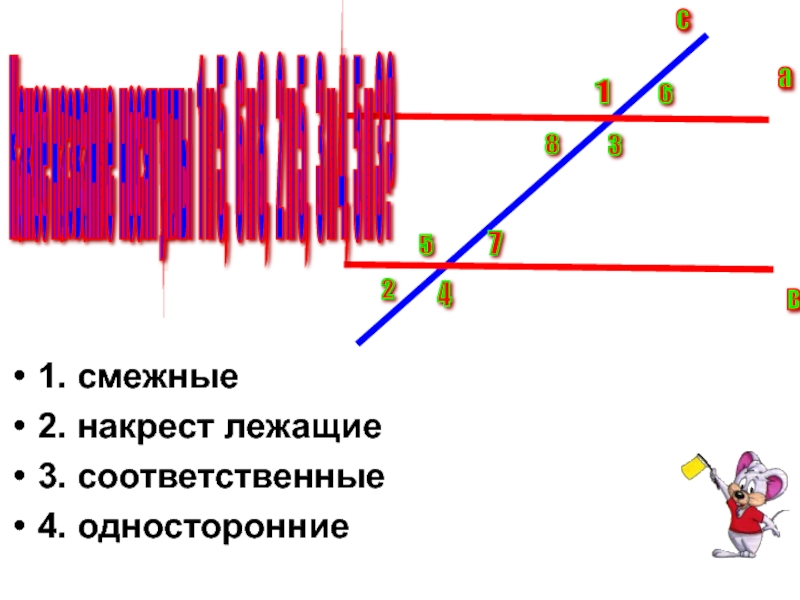
Слайд 4Какое название носят углы 1 и 5, 6 и
8, 2 и 5, 3 и 4, 5
и 3 ?
1. смежные
2. накрест лежащие
3. соответственные
4. односторонние
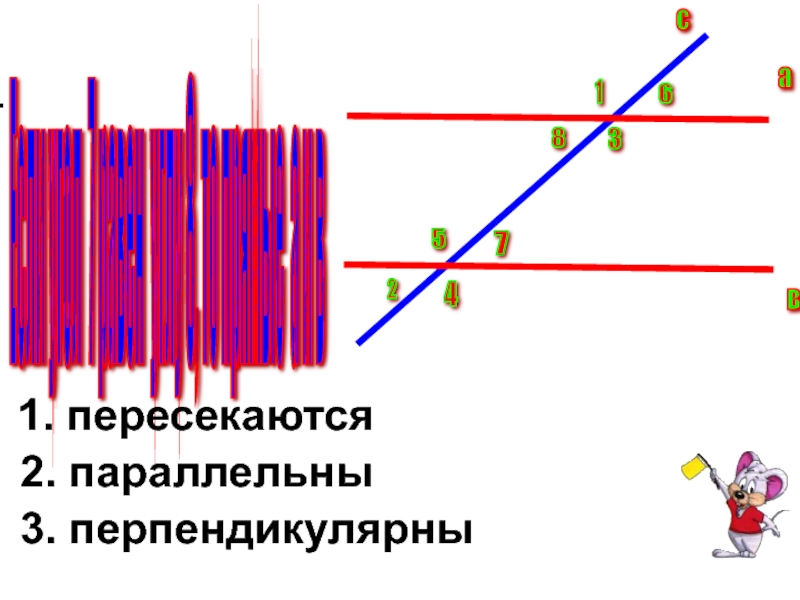
Слайд 5Если угол 7 равен углу 8, то прямые а и
в
. 1. пересекаются
2. параллельны
3. перпендикулярны
Слайд 7Через точку М, не лежащую на прямой а можно провести
1) две прямых, параллельных а
2) бесконечное множество прямых,параллельных а
3) одну прямую, параллельную а
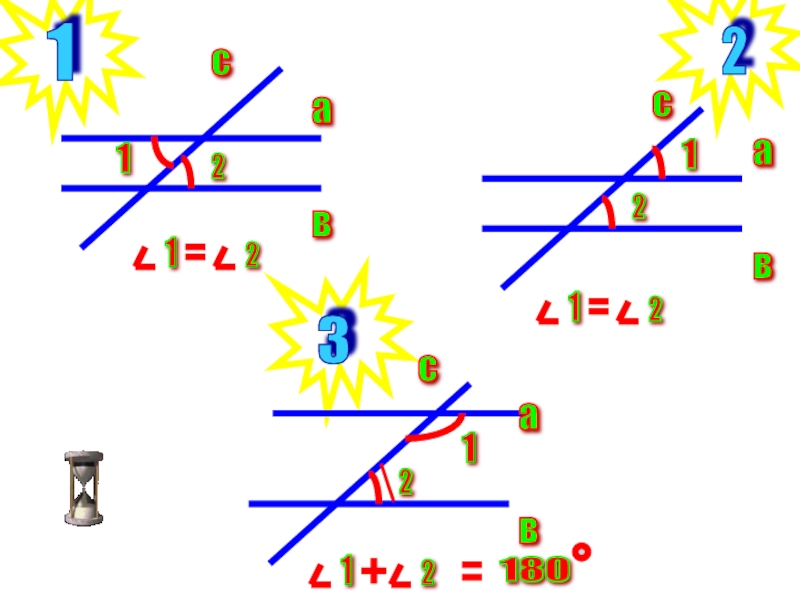
Если а // в и с // в, то
1) а пересекает с
2) а перпендикулярна с
3) а // с
Слайд 8Через точку, не лежащую на данной прямой, проходит только одна
прямая, параллельная данной
Если две прямые параллельны третьей прямой, то
они параллельны Верное утверждение:
Слайд 17Евклид (III век до н. э.) Древнегреческий математик, автор первого трактата
по геометрии «Начала» (в 13 книгах).
В основе всей геометрии греческого
математика ЕвклидаВ основе всей геометрии греческого математика Евклида В основе всей геометрии греческого математика Евклида лежало несколько простых первоначальных утверждений (аксиом), которые принимались за истинные без доказательств. Из аксиом путем доказательств выводились более сложные утверждения, из тех выводились еще более сложные. Особый интерес математиков всегда вызывала пятая аксиома о параллельных прямых. В отличие от остальных аксиом элементарной геометрии, аксиома параллельных не обладает свойством непосредственной очевидности. Поэтому на всем протяжении истории геометрии имели место попытки доказать аксиому параллельных, то есть вывести ее из остальных аксиом геометрии.
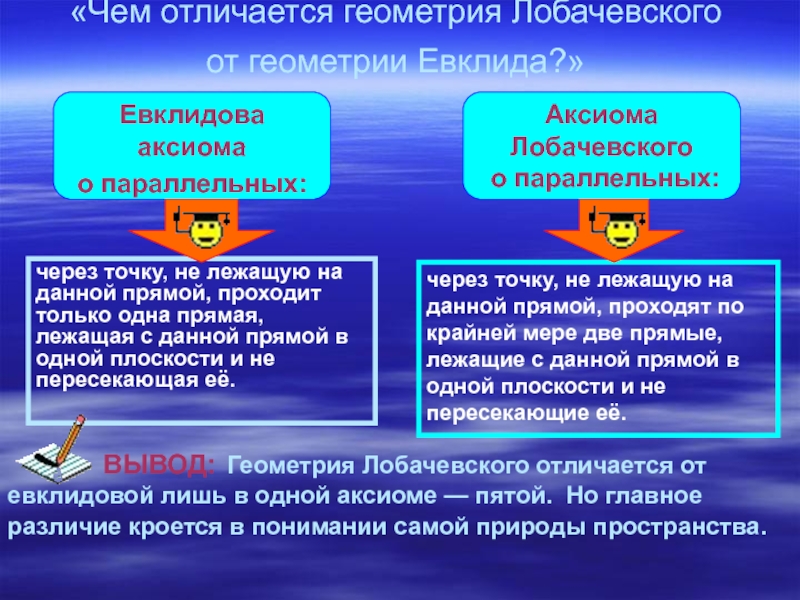
Слайд 18«Чем отличается геометрия Лобачевского
от геометрии Евклида?»
через точку, не лежащую
на данной прямой, проходит только одна прямая, лежащая с данной
прямой в одной плоскости и не пересекающая её.через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
ВЫВОД: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме — пятой. Но главное различие кроется в понимании самой природы пространства.
Евклидова аксиома
о параллельных:
Аксиома
Лобачевского
о параллельных:
Слайд 19Николай Иванович Лобачевский
(1792 – 1856 гг.)
Все! Перечеркнуты “Начала”.
Довольно мысль
на них скучала,
Хоть прав почти во всем Евклид,
Но
быть не вечно постоянству: И плоскость свернута в пространство,
И мир
Иной имеет вид...
Слайд 23
Этим способом пользуются в чертежной практике.
Способ построения параллельных прямых с
помощью
рейсшины.
Слайд 24Практическая работа
1) Постройте с помощью
линейки и треугольника три параллельные прямые: а,в,с
2)Постройте треугольник АВС и проведите прямую ВМ, проходящую через вершину В, параллельно прямой АС.Слайд 29
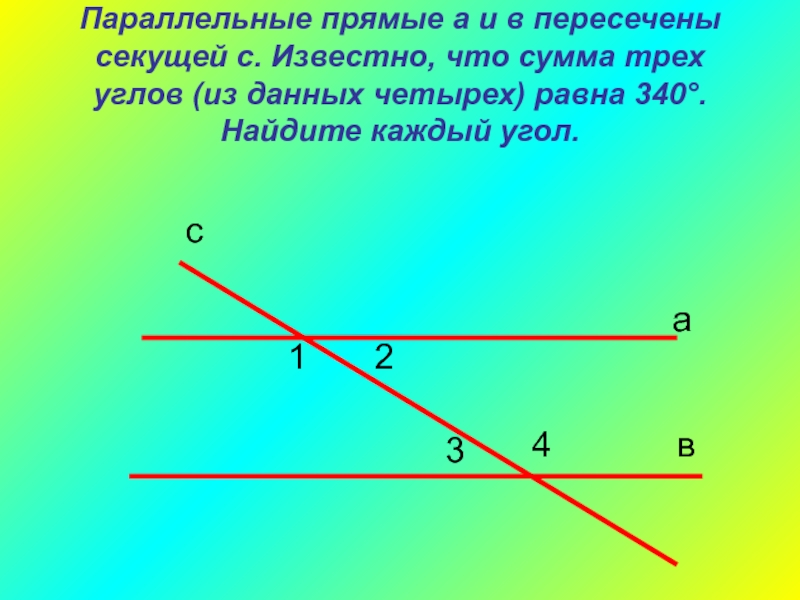
Параллельные прямые а и в
пересечены секущей с. Известно, что сумма трех углов (из данных
четырех) равна 340°. Найдите каждый угол.Слайд 31
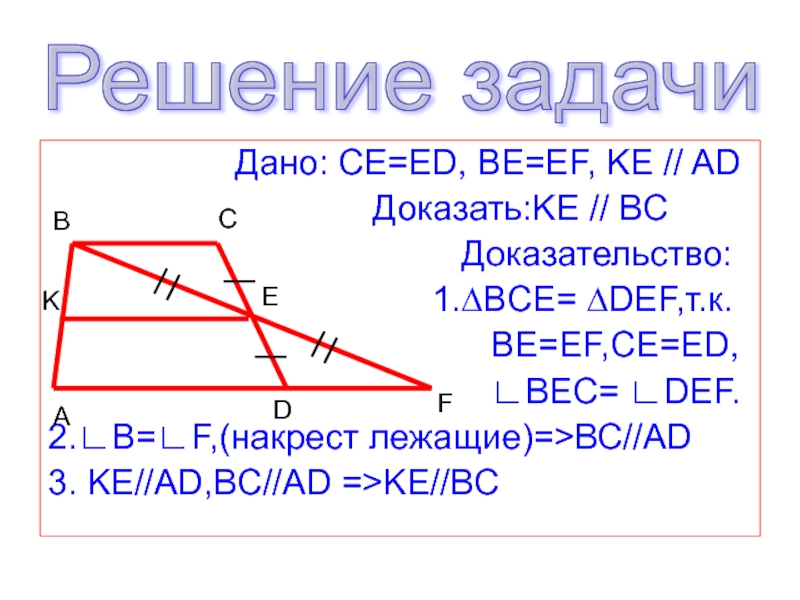
Дано: CE=ED, BE=EF, KE // AD
Доказать:KE // BCДоказательство:
1.∆BCE= ∆DEF,т.к.
BE=EF,CE=ED,
∟BEC= ∟DEF.
2.∟B=∟F,(накрест лежащие)=>ВС//AD
3. KE//AD,BC//AD =>KE//BC
Решение задачи
B
C
E
A
D
F
K
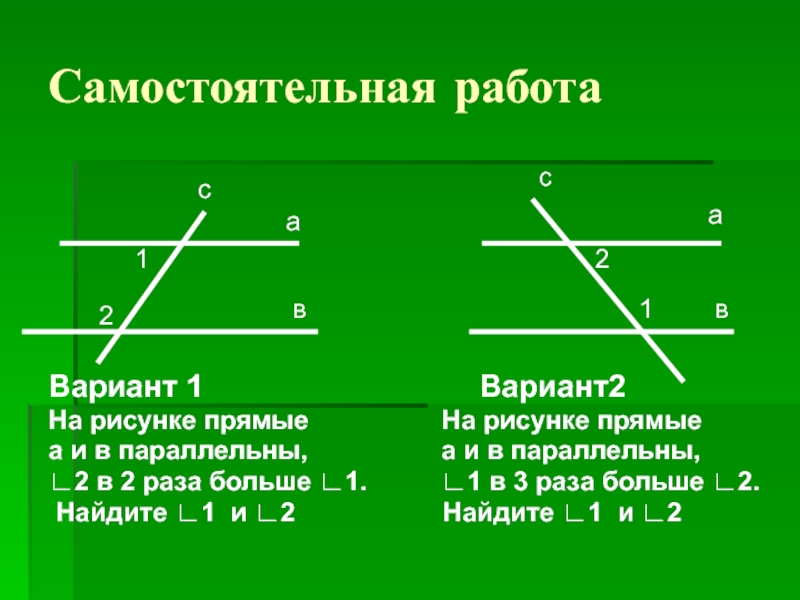
Слайд 33Самостоятельная работа
Вариант 1
Вариант2
На рисунке
прямые На рисунке прямые а и в параллельны, а и в параллельны,
∟2 в 2 раза больше ∟1. ∟1 в 3 раза больше ∟2.
Найдите ∟1 и ∟2 Найдите ∟1 и ∟2
1
2
1
2
а
в
в
с
с
а