Объем наклонной призмы

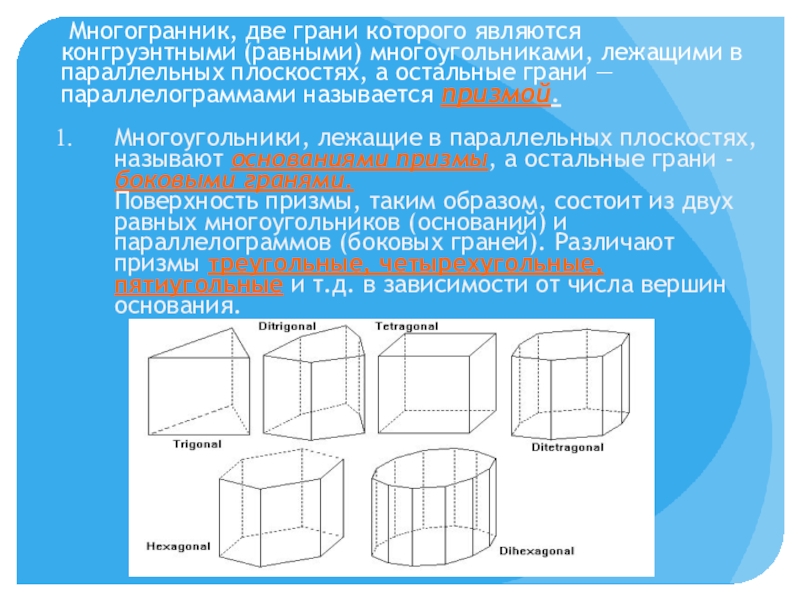
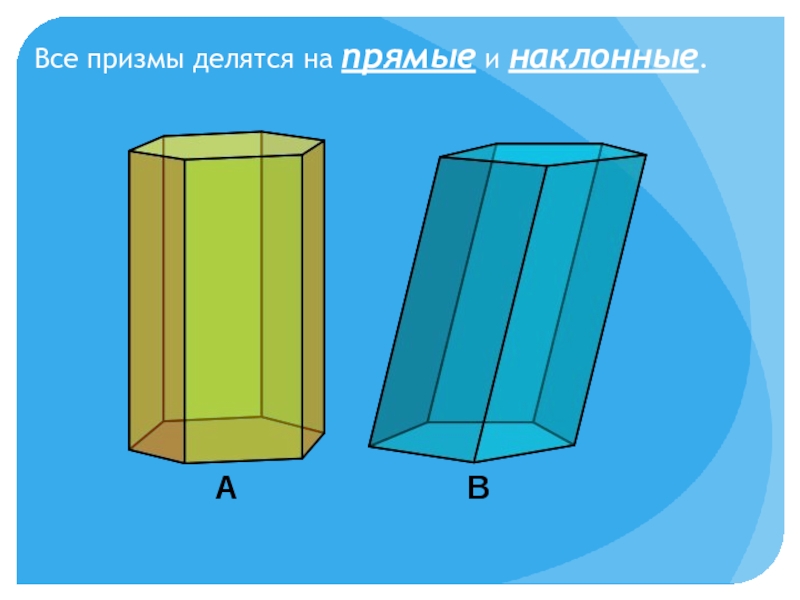
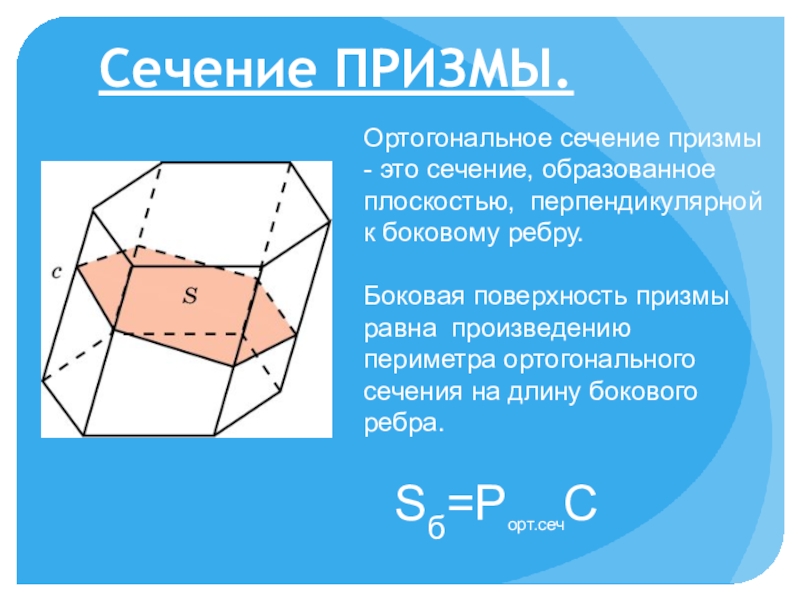
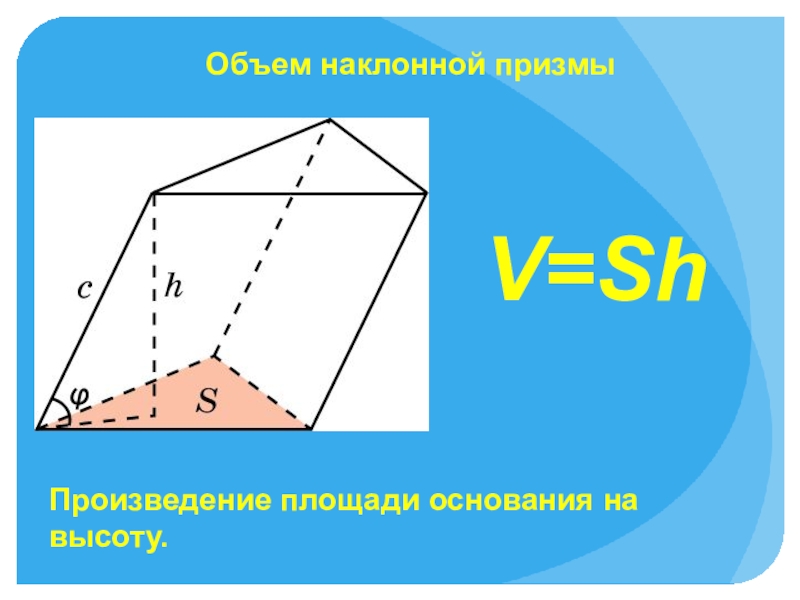
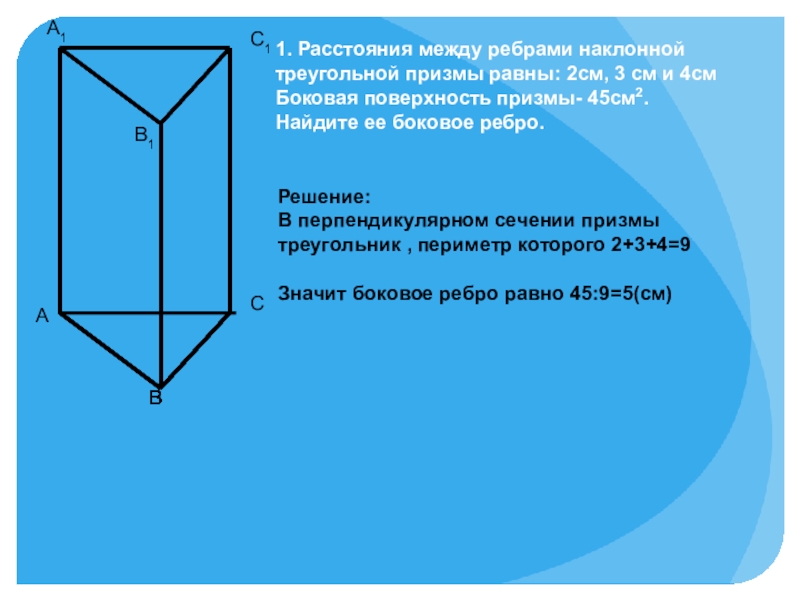
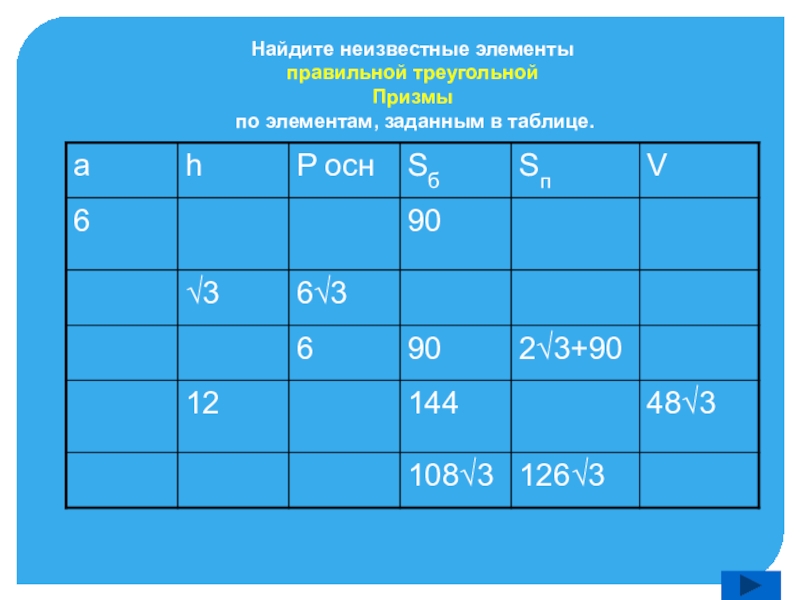
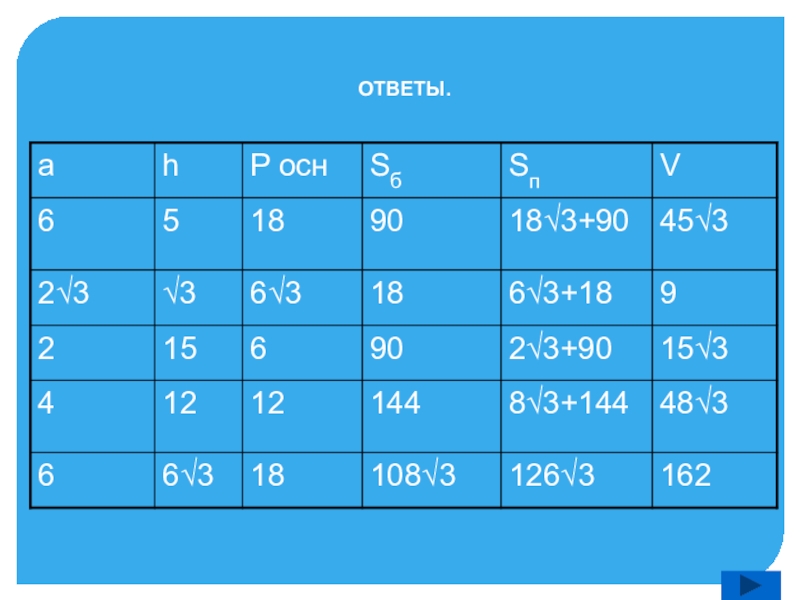
из которых две противоположные равны и параллельны, остальные же - параллелограммы”.

В 18 веке Тейлор дал такое определение призмы - это многогранник, у которого все грани кроме двух, параллельны одной прямой.

Брук Тэйлор (1685—1731) - английский математик

Термин “призма” греческого происхождения и буквально означает “отпиленное”
тело

плоскостях, а остальные грани — параллелограммами называется призмой.
Многоугольники, лежащие в параллельных

плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями. Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.

являются параллелограммами.

3. Боковые ребра призмы равны.

правильной призмой.

Свойства правильной призмы :
1. Основания правильной

призмы являются правильными многоугольниками. 2. Боковые грани правильной призмы являются равными прямоугольниками. 3. Боковые ребра правильной призмы равны.

к боковому ребру.

Боковая поверхность призмы равна произведению периметра ортогонального

сечения на длину бокового ребра.

Sб=Pорт.сечC

и 4см
Боковая поверхность призмы- 45см2.Найдите ее боковое ребро.
Решение:
В перпендикулярном сечении

призмы треугольник , периметр которого 2+3+4=9

Значит боковое ребро равно 45:9=5(см)

B

B

B

B

B

B

B

A

C

таблице.