Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обратные тригонометрические функции
Содержание
- 1. Обратные тригонометрические функции
- 2. Историческая справкаТригонометрические функции возникли впервые в связи
- 3. Для тригонометрических функций
- 4. Почему можно определить обратную тригонометрическую функцию.
- 5. Арксинус Арксинус
- 6. Слайд 6
- 7. АрктангенсАрктангенс
- 8. АрккотангенсАрккотангенс
- 9. Преобразований сумм обратных тригонометрических функцийНа промежутке
- 10. Уравнения и неравенства, левая и правая части
- 11. ПримерыПример 1. Решить уравнение Решение. Уравнение равносильно
- 12. Пример 2. Решить неравенство 3arcsin 2x < 1. Решение.
- 13. IIЗамечание. Какой из двух равносильных систем пользоваться
- 14. Пример 3. Решить неравенство Решение.Ответ: {– 2}.
- 15. Пример 4. Решить уравнение Решение. Так как
- 16. III а) arctg f(x) = arctg g(x)
- 17. Пример 5. Решить неравенство Решение. Неравенство равносильно следующему:
- 18. Уравнения и неравенства, левая и правая части
- 19. Рассуждая аналогично, можно получить следующие переходы:Замечание. Корнем
- 20. Пример 6. Решить уравнение Решение. Корень
- 21. Пример 7. Решить уравнение Решение. Корень x = – 2 является посторонним.Ответ:
- 22. Пример 8. Решить уравнение arctg (2sin x)
- 23. При решении неравенств, левая и правая части
- 24. 3) Решим неравенство f(x)
- 25. При решении уравнений и неравенств данного типа,
- 26. Замена переменнойНекоторые уравнения и неравенства, содержащие обратные
- 27. Пример 11.
- 28. Пример 12. Решить уравнение
- 29. IV. Использование свойств монотонности и ограниченности обратных
- 30. Пример 13. Решить
- 31. Пример 15. Решить неравенство
- 32. Пример 16. Решить уравнение
- 33. Уравнения и неравенства с параметрами.
- 34. Пример 2. Решить неравенство с параметром a:
- 35. Пример 3. Решить уравнение с параметром a:
- 36. Список используемой литературы1. Коломогоров «алгебра начало анализа»2. Вельмушкина, Н.
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Обратные тригонометрические функции
Работу выполнила:
Ученица 10 А класса
МОУ «Гимназии №125»
Щепеткова Дарья
Рук.
Чикрин Е.А.
Слайд 2Историческая справка
Тригонометрические функции возникли впервые в связи с исследованиями в
астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся
по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции – ЕвклидаТригонометрические функции возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу тригонометрическими функциями, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции – Евклида, Архимеда, Аполлония Пергского и других.В последующий период математика долгое время наиболее активно развивалась индийскими и арабсками учеными. В трудах по астрономии Ариабхаты появляется термин «ардхаджива». Позднее привилось более краткое название «джива», а при переводе математических терминов в XII в. Это слово было заменено латинским «sinus».
Принципиальное значение имело составление Птолемеем первой таблицы синусов(долгое время она называлась таблицей хорд): появилось практическое средство решения ряда прикладных задач, и в первую очередь задач астрономии.
Слово косинус –это сокращение латинского выражения «complementy sinus»(синус).
Тангенсы возникли в связи с решением задачи об определении длины тени.Тангенс (а также котангенс, секанс и косеканс) введен в X веке Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты в XIV в. Т. Бравердином, а позже астрономом Региомонтаном.
Первым автором, который использовал специальные символы для обратных тригонометрических функций был, Бернулли. В 1729 и в1736 годах он писал as и at соответственно вместо arcsin и arctg.Современные обозначения arcsin и arctg появляются в 1772 г. в работах венского математика Шерфера известного французского ученого Лагранжа.Приставка «arc» происходит от латинского «arcus»(лук, дуга), что вполне согласуется со смыслом понятия: arcsin x, например,- это угол (а можно сказать и дуга) синус которого равен x.
Слайд 3Для тригонометрических функций
можно определить обратные функции
(круговые функции, аркфункции). Они обозначаются соответственно , , , .К обратным тригонометрическим функциям обычно относят шесть функций:
аркси́нус (обозначение: arcsin)
аркко́синус (обозначение: arccos)
аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
арксе́канс (обозначение: arcsec)
арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Слайд 4Почему можно определить обратную тригонометрическую функцию.
Теорема о корне:
Пусть функция f возрастает (или убывает) на промежутке I, число a – любое из значений, принимаемых f на этом промежутке. Тогда уравнение F(x)=a имеет единственный корень в промежутке I.На промежутке функция монотонна, возрастает, т.е.
все значения от -1 до 1 принимает ровно один раз, поэтому можно определить обратную функцию - arcsin x.
На промежутке функция монотонна, убывает, т.е.
принимает все значения от -1 до 1 ровно один раз, поэтому можно определить обратную тригонометрическую функцию.
На интервале функция монотонна, возрастает и принимает все значения из R ровно один раз, поэтому можно определить обратную тригонометрическую функцию.
На интервале функция монотонна, убывает , принимает все значения из R ровно один раз, поэтому мы можем определить обратную тригонометрическую функцию.
Слайд 5 Арксинус
Арксинус
-угол
из промежутка синус которого равен а.Если , то
Функция y = arcsinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.
--функция нечетная
Таким образом, arcsina, (arctga) - угол первой четверти, если a - положительно, и угол четвертой четверти, если a - отрицательно.
,
Слайд 6 Арккосинус
Арккосинус
-угол из
промежутка, косинус которого равен а.
Если , то
Функция y = arccosx непрерывна и ограничена на всей своей числовой прямой.
Функция y = arccosx является строго убывающей.
arccosa (arctga) - угол первой четверти, если a - положительно, и угол второй четверти, если a - отрицательно.
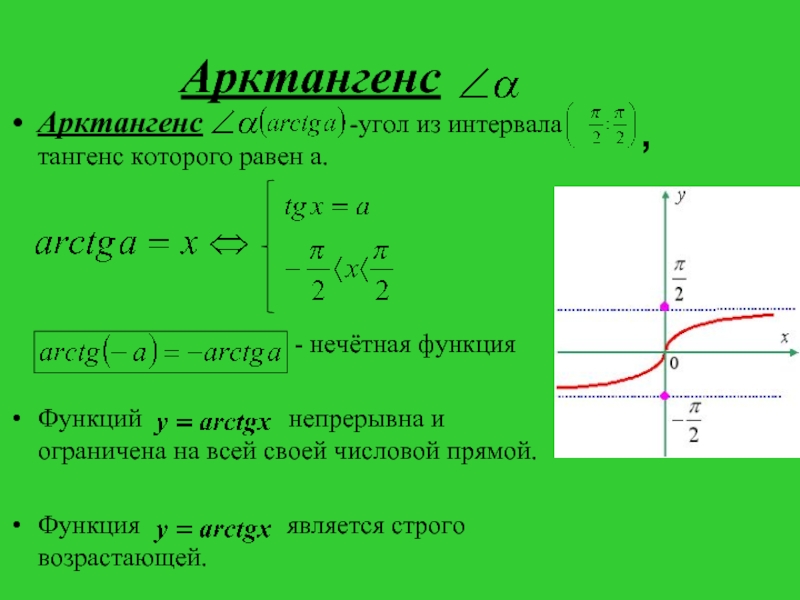
Слайд 7 Арктангенс
Арктангенс
-угол из интервала
тангенс которого равен а.- нечётная функция
Функций непрерывна и ограничена на всей своей числовой прямой.
Функция является строго возрастающей.
,
Слайд 8 Арккотангенс
Арккотангенс
-угол из интервала
, котангенскоторого равен а.
Функция непрерывна и ограничена на всей своей
числовой прямой.
Функция является строго убывающей.
Слайд 9Преобразований сумм обратных тригонометрических функций
На промежутке
функция возрастает, т.е. каждое свое значение
принимает ровно один раз, т.е. если на промежутке .
;
Аналогично:
Слайд 10Уравнения и неравенства, левая и правая части которых являются одноименными
обратными тригонометрическими функциями
Решение уравнений и неравенств, левая и правая части
которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность( функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения). Поэтому справедливы следующие равносильные переходы.
I
Замечание. Какой из двух равносильных систем пользоваться при решении уравнений 1а), зависит от того, какое неравенство проще: | f(x) | £ 1 (тогда используем первую систему), или | g(x) | £ 1 (в этом случае используем вторую систему).
Слайд 11Примеры
Пример 1. Решить уравнение
Решение. Уравнение равносильно системе:
Замечание. Решать неравенство,
входящее в систему не обязательно. Достаточно проверить, удовлетворяют ли неравенству
найденные корни уравнения.Слайд 13II
Замечание. Какой из двух равносильных систем пользоваться при решении уравнений
2а), зависит от того, какое неравенство проще: | f(x) | £ 1
(тогда используем первую систему), или | g(x) | £ 1 (в этом случае используем вторую систему).Слайд 15Пример 4. Решить уравнение
Решение. Так как
, то имеет место следующая цепочка равносильных преобразований:
Слайд 16III
а) arctg f(x) = arctg g(x) f(x) =
g(x);
б) acrtg f(x) ≤ arctg g(x) f(x) ≤ g(x).
а) arcctg f(x)
= arcctg g(x) f(x) = g(x);
б) arcctg f(x) ≤ arcctg g(x) f(x) ≥ g(x).IV
Слайд 18Уравнения и неравенства, левая и правая части которых являются разноименными
обратными тригонометрическими функциями
При решении уравнений и неравенств, левая и
правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x0 – решение этого уравнения. Обозначим arcsin f(x0) = arccos g(x0) через a.
Тогда sin a = f(x0), cos a = g(x0),
откуда
Итак, arcsin f(x) = arccos g(x) (1)
Слайд 19Рассуждая аналогично, можно получить следующие переходы:
Замечание. Корнем каждого из уравнений
(1)–(4) может быть только такое число x0, для которого
и .В противном случае множество значений левой и правой частей уравнения не пересекаются.
Слайд 22
Пример 8. Решить уравнение arctg (2sin x) = arcctg (cos
x).
Решение.
Корни вида
являются посторонними.Ответ:
Слайд 23При решении неравенств, левая и правая части которых представляют собой
разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в
некоторых случаях учитывать свойства монотонных функций.Пример 9. Решить неравенство
Решение. Рассмотрим функцию
и решим неравенство f(x) ≤ 0 методом интервалов.
1) Найдем D(f). Для этого решим систему
2) Найдем нули f(x). Для этого решим уравнение
Корень x = – 2 является посторонним
Слайд 24
3) Решим неравенство f(x) ≤ 0 методом
интервалов.
Замечание 4. Заметим, что найдя корень уравнения
можно было не
обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция
монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.
Слайд 25При решении уравнений и неравенств данного типа, содержащих параметры, становится
актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными,
следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,Слайд 26Замена переменной
Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно
свести к алгебраическим, сделав соответствующую замену переменной. При этом следует
помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.Пример 10. Решить уравнение
Решение. Обозначим
После преобразований получим уравнение
Поскольку
откуда
Ответ:
Слайд 27
Пример 11.
Решить неравенство
Решение. Пусть arccos x = t, 0 ≤ t
≤ π. ТогдаПоскольку
откуда
Ответ: [– 1; cos 2] И [cos 1; 1].
Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества
Слайд 28Пример 12.
Решить уравнение
Решение. Данное уравнение
равносильно следующему:
Пусть arcsin x = t,
Тогда
Слайд 29IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций
Решение
некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно
на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.
Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.
Теорема 3. Если то на множестве X уравнение f(x) = g(x) равносильно системе
Слайд 30 Пример 13. Решить уравнение 2arcsin 2x =
3arccos x.
Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция
y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.Ответ: {0,5}.
Пример 14. Решить уравнение
Решение. Пусть Тогда уравнение примет вид
Функции являются монотонно возрастающими.
Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение
имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому
Ответ: {– 1; 0}.
Слайд 31
Пример 15. Решить неравенство
Решение.
Левая
часть неравенства представляет собой монотонно
убывающую на отрезке
функциюУравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения.
Поэтому решением неравенства
является отрезок
Ответ:
Слайд 32Пример 16. Решить уравнение
arcsin (x(x + y)) +
arcsin (y(x + y)) = .Решение. Поскольку arcsin
то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно Таким образом, уравнение равносильно системе:
Решение последней системы не представляет труда.
Слайд 33Уравнения и неравенства с параметрами.
Пример 1. Решить
уравнение с параметром a:
Решение. Уравнение равносильно уравнению
Рассмотрим два случая:1) a = 0. В этом случае система примет вид:
2) a ≠ 0. В этом случае уравнение системы является квадратным. Его корни:
Так как | x | ≤ 1, то
Если a = – 1, то Если то уравнение имеет два корня.
Ответ:
при при a = – 1 и a = 0 x = 1;
при прочих a решений нет.
Слайд 34Пример 2. Решить неравенство с параметром a:
Решение. Неравенство равносильно
системе
Решать последнюю систему можно графо-аналитическим методом, учитывая то, что
при a > первое неравенство системы равносильно неравенству x ≥ 1, при a < – неравенству x ≥ 1,
при a = решением первого неравенства является любое действительное число.
Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.
Ответ:
при | a | > решений нет;
при a =– x = 1;
Слайд 35Пример 3. Решить уравнение с параметром a:
arcctg (x – 2a) = arctg (2x – a).
Решение. Данное уравнение равносильно
системе Графиком квадратного трехчлена
является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 < 0, то
при любом a уравнение f(x) = 0 имеет ровно 2 корня, между которыми и заключено число 2a.
Поэтому только больший корень f(x) удовлетворяет условию x > 2a.
Это корень
Ответ: при любом a
Слайд 36Список используемой литературы
1. Коломогоров «алгебра начало анализа»
2. Вельмушкина, Н. Уравнения, содержащие обратные
тригонометрические функции [Текст] / Н. Вельмушкина // Математика / Прил.
к ПС, 2004. – №6. – С.26-27.3. В.С. Крамор, П.А Михайлов " Тригонометрические функции ." Москва "Просвещение " 1983г.
4. В. Н. Литвиненко, А. Г. Мордкович . " Практикум по решению математических задач. " Москва "Просвещение " 1984г.
5. А.П. Ершова , В. В. Голобородько " Алгебра . Начала анализа. " "ИЛЕКСА " Москва 2003г
6. Кожеуров, П.Я. Тригонометрия [Текст] / П.Я. Кожеуров. – М.: Физматгиз, 1963. – 320с.
7. Савин, А. Тригонометрия [Текст] / А. Савин // Квант, 1996. – №4.













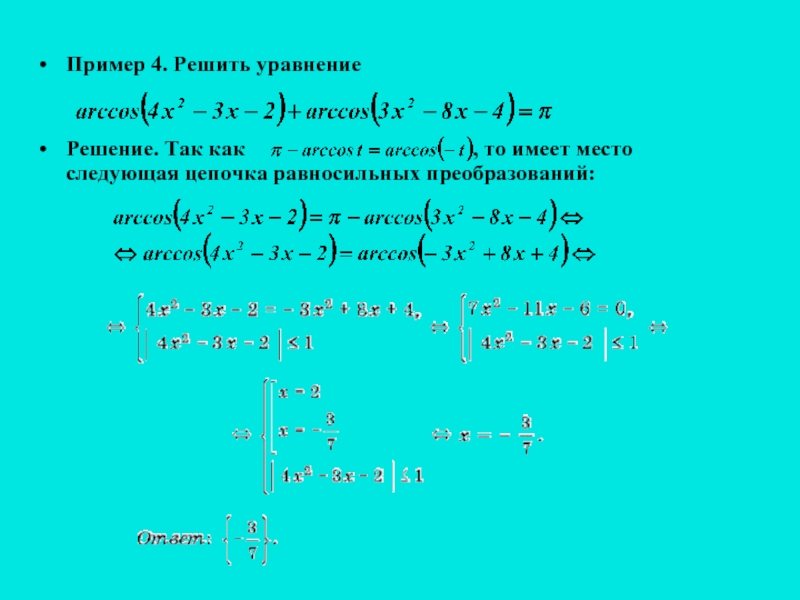




















![Обратные тригонометрические функции Список используемой литературы1. Коломогоров «алгебра начало анализа»2. Вельмушкина, Н. Уравнения, содержащие обратные тригонометрические Список используемой литературы1. Коломогоров «алгебра начало анализа»2. Вельмушкина, Н. Уравнения, содержащие обратные тригонометрические функции [Текст] / Н. Вельмушкина //](/img/thumbs/ed8a65d679c82bf37d9f1d51f4a7ab40-800x.jpg)