Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описательная статистика
Содержание
- 1. Описательная статистика
- 2. Среднее значение.Определение: Средним
- 3. Таблица 1. Производство пшеницы в России в
- 4. Таблица 2. Урожайность зерновых культур в России
- 5. Таблица 3. Население шести крупнейших городов Московской
- 6. Медиана.Определение: Медианой набора чисел называют такое число,
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Наибольшее и наименьшее
- 11. Таблица 7. Производство зерна в России.Найти наибольшее,
- 12. Слайд 12
- 13. Слайд 13
- 14. Таблица 8. Производство пшеницы в России в
- 15. Слайд 15
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Среднее значение.
Определение: Средним арифметическим нескольких чисел
называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а в знаменателе – их количество.Слайд 3Таблица 1. Производство пшеницы в России в 1995-2001гг.
(30,1+34,9+44,3+27,0+31,0+34,5+47,0):7 ≈ 35,5.
Получаем,
что среднее производство пшеницы в России за рассматриваемый период 1995-2001гг.
Составляло приблизительно 35,5 млн. тонн в год.Слайд 4Таблица 2. Урожайность зерновых культур в России в 1992-2001 гг.
а)Средняя
урожайность зерновых культур в России за 1992-1996гг.
(18,0+17,1+15,3+13,1+14,9):5 ≈ 15,68.
б)Средняя урожайность
зерновых культур в России за 1997-2001гг.(17,8+12,9+14,4+15,6+19,4):5 ≈ 16,02.
в)Средняя урожайность зерновых культур в России за 1992-2001гг.
(18,0+17,1+15,3+13,1+14,9+17,8+12,9+14,4+15,6+19,4):10 ≈ 15,85.
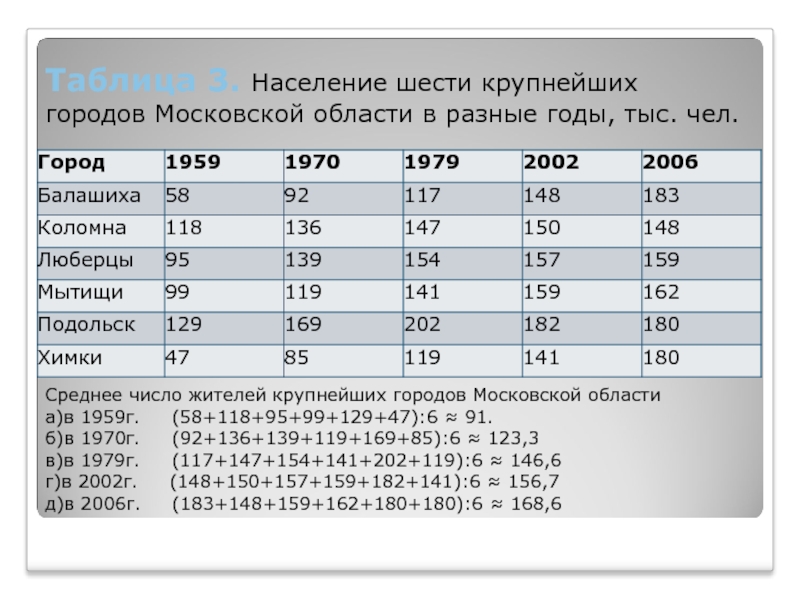
Слайд 5Таблица 3. Население шести крупнейших городов Московской области в разные
годы, тыс. чел.
Среднее число жителей крупнейших городов Московской области
а)в
1959г. (58+118+95+99+129+47):6 ≈ 91.б)в 1970г. (92+136+139+119+169+85):6 ≈ 123,3
в)в 1979г. (117+147+154+141+202+119):6 ≈ 146,6
г)в 2002г. (148+150+157+159+182+141):6 ≈ 156,7
д)в 2006г. (183+148+159+162+180+180):6 ≈ 168,6
Слайд 6Медиана.
Определение: Медианой набора чисел называют такое число, которое разделяет набор
на две равные по численности части.
Пример 1. Возьмём какой-нибудь набор
различных чисел, например 1,4,7,9,11.Медианой в этом случае оказывается число, стоящее в точности посередине, m=7.
Пример 2. Рассмотрим набор 1,3,6,11. Медианой этого набора служит любое число, которое больше 3 и меньше 6. По определению в качестве медианы в таких случаях берут центр срединного интервала. В нашем случае это центр интервала (3,6). Это полусумма его концов
(3+6):2=4,5
Медианой этого набора считают число 4,5.
Слайд 7
Пример 3. Таблица 4. Производство пшеницы в России в
1995-2001гг.Средний урожай 35,5 млн. тонн в год. Вычислим медиану. Упорядочим числа:
27,0; 30,1; 31,0; 34,5; 34,9; 44,3; 47,0.
Медиана равна 34,5 млн. тонн (урожай 2000г.)
Слайд 8 Пример
4.
Найти медиану следующих наборов чисел
а)2,4,8,9 (4+8):2=6
m=6б)1,3,5,7,8,9 (5+7):2=6 m=6
в)10,11,11,12,14,17,18,22
(12+14):2=13 m=13
Слайд 9 Пример 5.
Таблица 5. Урожайность зерновых культур в России в 1992-2001гг.
По данным
таблицы вычислить медиану урожайности и среднюю урожайность зерновых культур в России за период:а)1992-2001гг. m=(15,3+15,6):2=15,45
среднее ≈ 15,85
б)1992-1996гг. m=15,3
среднее ≈ 15,68
в)1997-2001гг. m=15,6
среднее ≈ 16,02
Слайд 10 Наибольшее и наименьшее
значение. Размах.
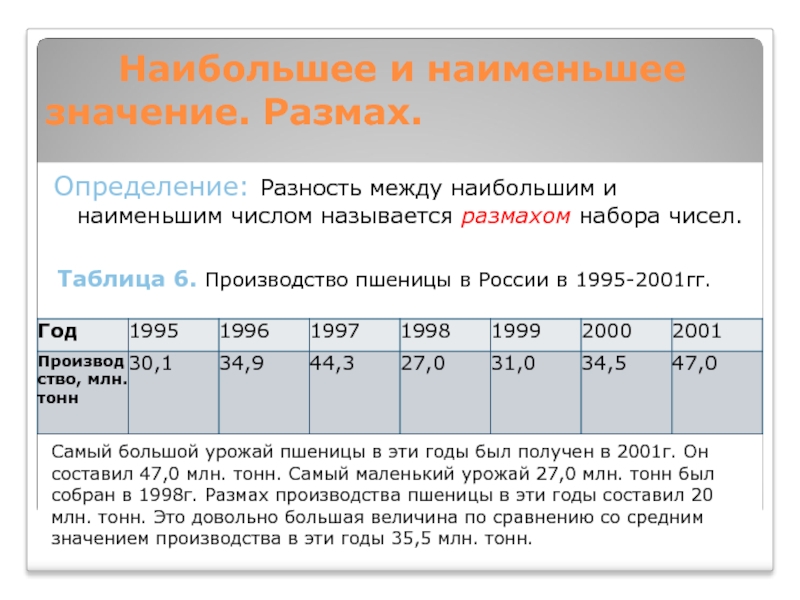
Определение: Разность между наибольшим
и наименьшим числом называется размахом набора чисел.Таблица 6. Производство пшеницы в России в 1995-2001гг.
Самый большой урожай пшеницы в эти годы был получен в 2001г. Он составил 47,0 млн. тонн. Самый маленький урожай 27,0 млн. тонн был собран в 1998г. Размах производства пшеницы в эти годы составил 20 млн. тонн. Это довольно большая величина по сравнению со средним значением производства в эти годы 35,5 млн. тонн.
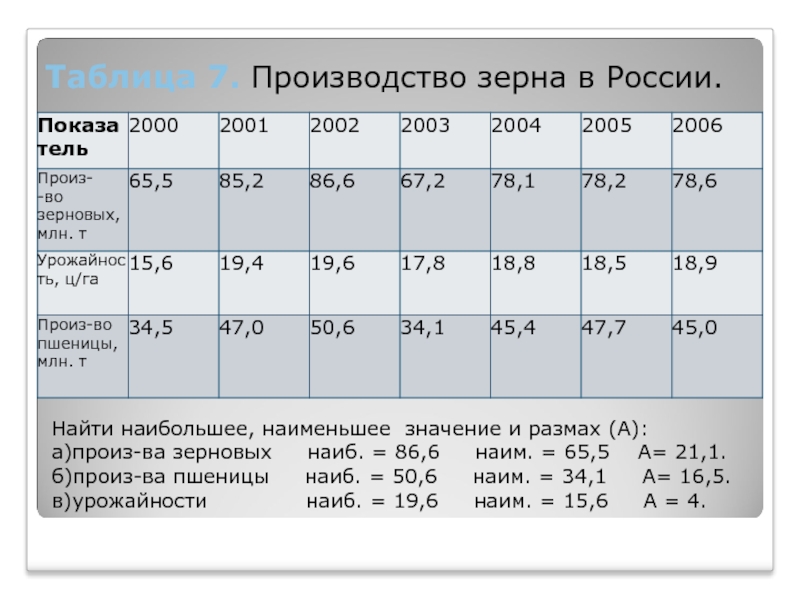
Слайд 11Таблица 7. Производство зерна в России.
Найти наибольшее, наименьшее значение и
размах (А):
а)произ-ва зерновых наиб. = 86,6
наим. = 65,5 А= 21,1.б)произ-ва пшеницы наиб. = 50,6 наим. = 34,1 А= 16,5.
в)урожайности наиб. = 19,6 наим. = 15,6 А = 4.
Слайд 12 Отклонения.
Определение: отклонение
– это разница между каждым числом набора и средним значением.
Пример:
возьмём набор 1,6,7,9,12. Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём отклонение каждого числа от среднего:1-7=-6, 6-7=-1, 7-7=0, 9-7=2, 12-7=5.
Сумма отклонений чисел от среднего арифметического этих чисел равна нулю.
Слайд 13 Дисперсия.
Определение:
среднее арифметическое квадратов отклонений от среднего значения называется в статистике
дисперсией набора чисел.Пример 1. Снова обратимся к таблице производства пшеницы в России. Мы нашли, что среднее производство пшеницы за период 1995-2001гг. составило 35,5 млн. тонн в год. Вычислим дисперсию. Составим таблицу, разместив данные по производству не в строке, а в столбце. Вычислим отклонения от среднего и их квадраты. Полученные числа занесём в два новых столбца.
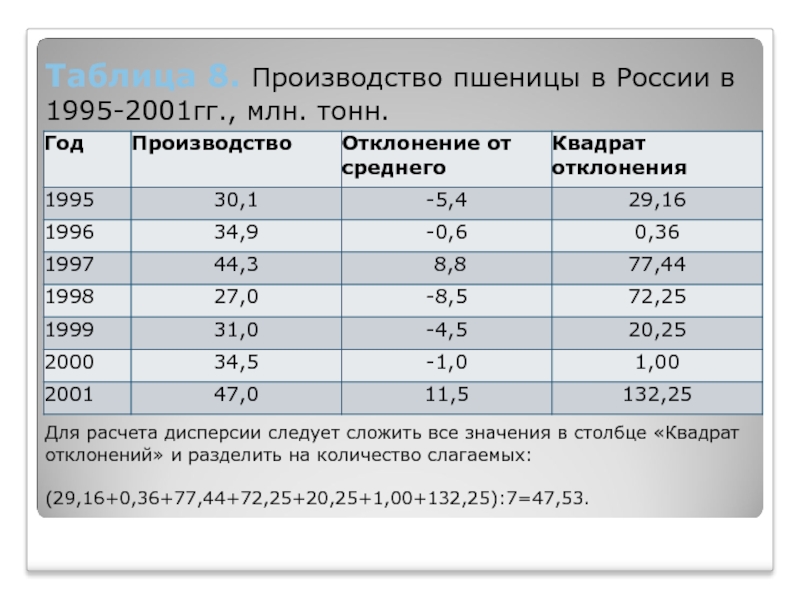
Слайд 14Таблица 8. Производство пшеницы в России в 1995-2001гг., млн. тонн.
Для
расчета дисперсии следует сложить все значения в столбце «Квадрат отклонений»
и разделить на количество слагаемых:(29,16+0,36+77,44+72,25+20,25+1,00+132,25):7=47,53.
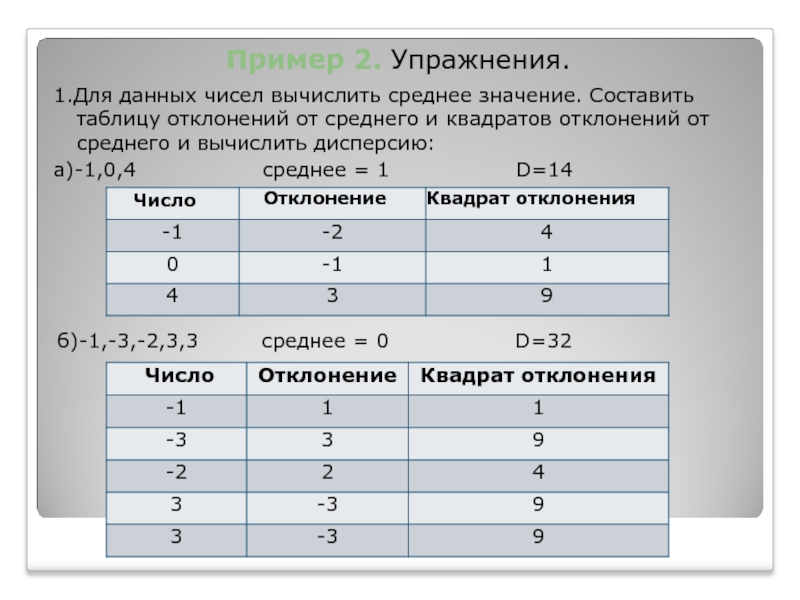
Слайд 15 Пример
2. Упражнения.
1.Для данных чисел вычислить среднее значение. Составить таблицу отклонений
от среднего и квадратов отклонений от среднего и вычислить дисперсию:а)-1,0,4 среднее = 1 D=14
б)-1,-3,-2,3,3 среднее = 0 D=32