Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
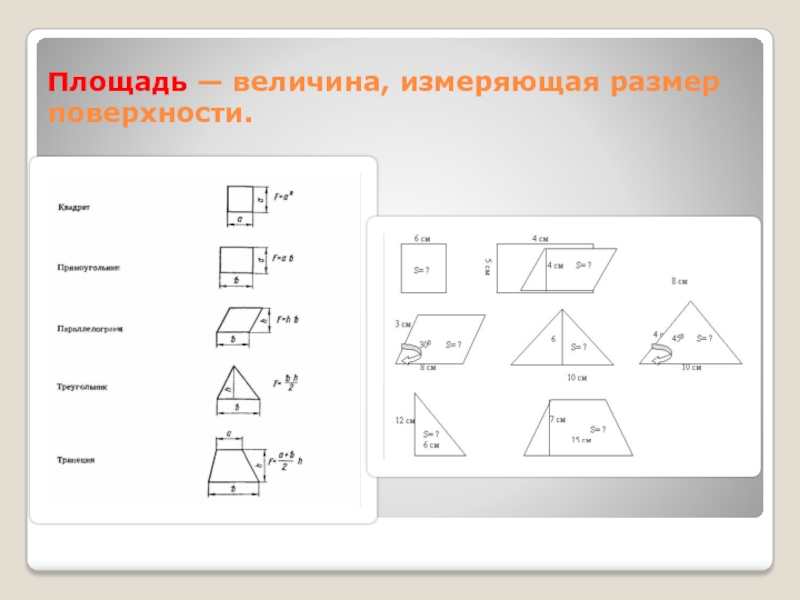
Определённый интеграл. Введение и некоторые его приложения
Содержание
- 1. Определённый интеграл. Введение и некоторые его приложения
- 2. Введение определённого интеграла
- 3. Пусть графически задана функция f(x), непрерывная на своей области определения D(f)y
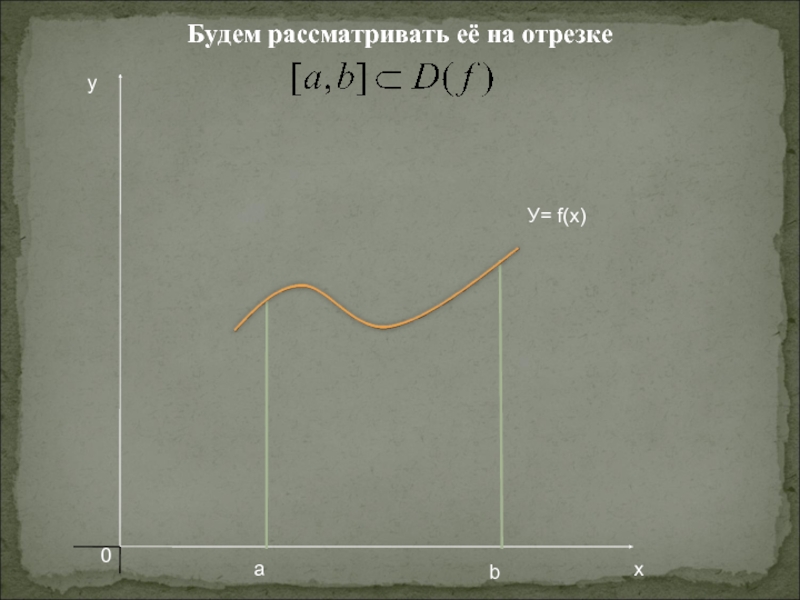
- 4. Будем рассматривать её на отрезкеyаb
- 5. Построим фигуру, ограниченную графиком функции y =
- 6. Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a
- 7. Каждой полосе поставим в соответствие прямоугольник, одна
- 8. Основание i-го прямоугольника равно разности xi+1-хi, которую
- 9. Площадь i-го прямоугольника равна:Сложив площади всех прямоугольников, получаем приближенное значение площади S криволинейной трапеции:
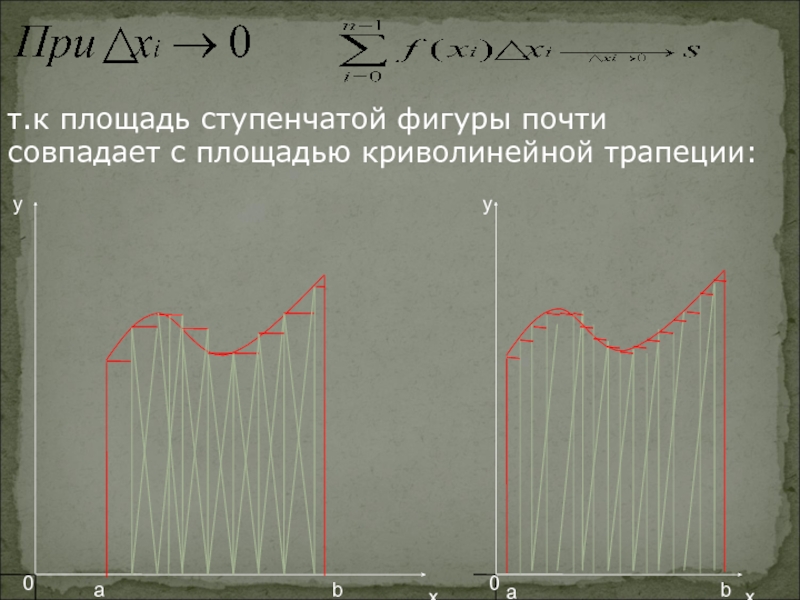
- 10. т.к площадь ступенчатой фигуры почти совпадает с площадью криволинейной трапеции:yabyab
- 11. Точное значение площади S получается как предел
- 12. Если предел функции f(x) существует, то f(x)
- 13. Некоторые приложения определённого интеграла
- 14. Задача Вычислить площадь фигуры F, ограниченной линиями y= 4-x2 и y= x2-2x1) Площадь плоской фигуры
- 15. Построим фигуру F. Для этого построим линии,
- 16. Найдем точки пересечения этих параболA(-1;3); B(2;0)Искомую площадь Sf можно найти как алгебраическую сумму площадей криволинейных трапеций
- 17. Слайд 17
- 18. 2) Объем тела вращенияПусть тело образуется при
- 19. ЗАДАЧАВычислить объем шара, получаемого вращением полуокружностивокруг оси
- 20. Авторские права принадлежат НОУ «Колледж Мосэнерго»Прикладная математика
- 21. Скачать презентанцию
Введение определённого интеграла
Слайды и текст этой презентации
Слайд 5Построим фигуру, ограниченную графиком функции y = f(x),
прямыми x
= а, x = в и у = 0. Назовём
её криволинейнойтрапецией ABCD
Поставим задачу нахождения её площади S
а
b
x=a
B
C
D
A
x=b
y=0
Слайд 6Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0=
a
а, у=х1, у = х2, …у = хi, y= xi+1,…, y= b. Этими прямыми трапеция ABCD разбивается на полосы.
x0
xn
![Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a](/img/thumbs/6205119b52e16586980376d47ad60df2-800x.jpg "Определённый интеграл. Введение и некоторые его приложения Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a")
Слайд 7Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть
отрезок [xi;xi+1], а смежная сторона – это отрезок f(xi) (i=0…n-1)
y
В
С
А
D
Криволинейная
трапеция заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольниковx0
xn
![Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок [xi;xi+1], а смежная сторона – это](/img/thumbs/8d6f5bda631d64ebcebc5a2ca832420a-800x.jpg "Определённый интеграл. Введение и некоторые его приложения Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок")
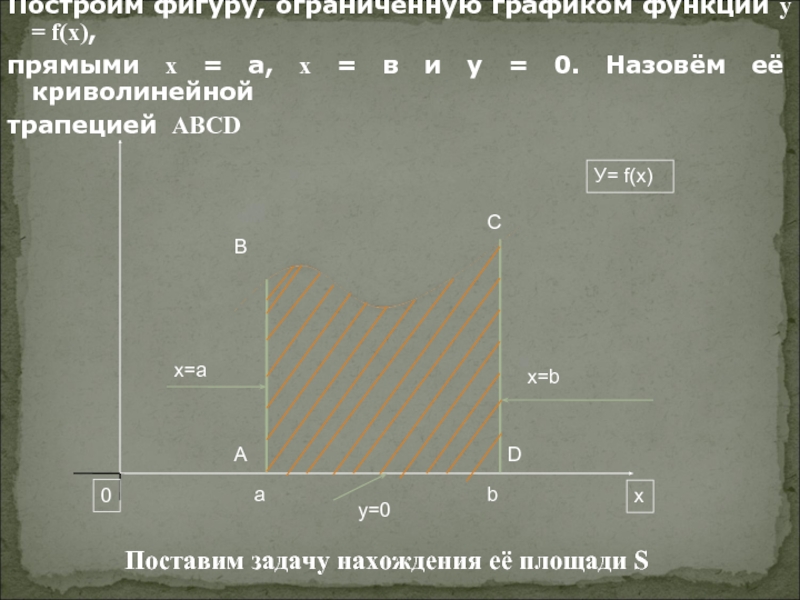
Слайд 8Основание i-го прямоугольника равно разности xi+1-хi, которую мы будем обозначать
через Высота i-го прямоугольника равна
f(xi)y
В
С
A
D
x0
xn
Слайд 9Площадь i-го прямоугольника равна:
Сложив площади всех прямоугольников,
получаем приближенное значение
площади S
криволинейной трапеции:
Слайд 11Точное значение площади S получается как предел суммы площадей всех
прямоугольников
Для обозначения предельных сумм вида
f(xi) xi немецкий учёный В.Лейбниц ввёл символ - интеграл функции f(x) от а до b
Слайд 12Если предел функции f(x) существует, то f(x)
называется интегрируемой на
отрезке [a,b].
Числа а и b называются нижним и верхним
пределом
интегрирования. При постоянныхпределах интегрирования определённый
интеграл
представляет собой определённое число.
![Если предел функции f(x) существует, то f(x) называется интегрируемой на отрезке [a,b].Числа а и b называются нижним](/img/thumbs/b88237bbef74566ce29da4eea114730a-800x.jpg "Определённый интеграл. Введение и некоторые его приложения Если предел функции f(x) существует, то f(x) называется интегрируемой на отрезке")
Слайд 14
Задача
Вычислить площадь фигуры F, ограниченной
линиями y= 4-x2 и
y= x2-2x
1) Площадь плоской фигуры
Слайд 15Построим фигуру F. Для этого построим
линии, ограничивающие эту фигуру
Решим задачу по следующему алгоритму:
D
2
1
B
C
A
4 Y
A1 0
-2
-1
X
Слайд 16Найдем точки пересечения этих парабол
A(-1;3); B(2;0)
Искомую площадь Sf можно найти
как алгебраическую сумму площадей криволинейных трапеций
Слайд 182) Объем тела вращения
Пусть тело образуется при вращении вокруг оси
OX криволинейной трапеции x1ABx2
Любое сечение этого тела плоскостью, перпендикулярной к
оси Ox будет круг, радиус которого равен соответствующей ординате точки кривой Y=f(x)Площадь сечения S(x) равна y2, т.е.
S(x)= f2(x)
Объем тела вращения может быть вычислен по формуле
Слайд 19ЗАДАЧА
Вычислить объем шара, получаемого вращением полуокружности
вокруг оси OX
Построим полуокружность
y
X
R
-R
R
При вращении этой полуокружности вокруг OX получается сфера, ограничивающая шар.
Объем шара найдем по формуле
Ответ: Объем шара (куб.ед.)
Теги
