Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямых в пространстве
Содержание
- 1. Параллельность прямых в пространстве
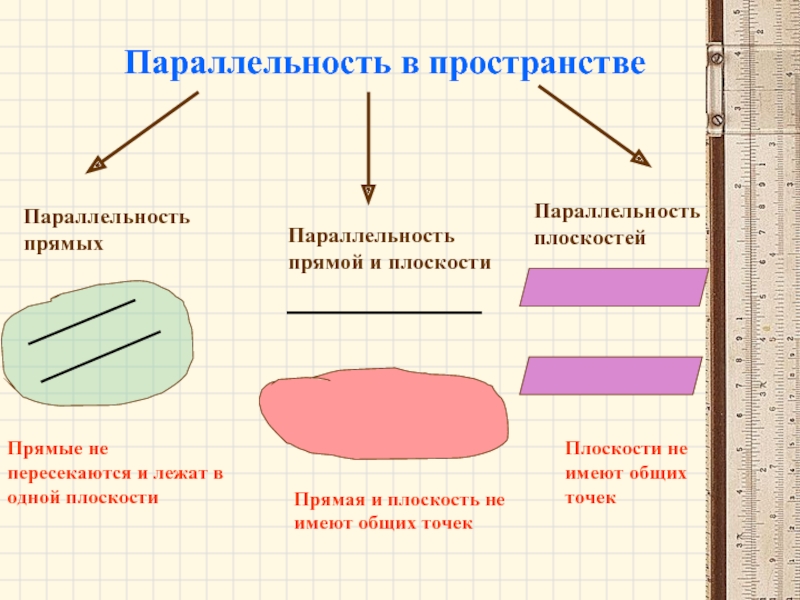
- 2. Параллельность в пространствеПараллельность прямыхПараллельность прямой и плоскостиПараллельность плоскостей
- 3. прямые в пространстве
- 4. свойство параллельных прямых в пространствеЧерез точку
- 5. Доказательство теоремы 16.1аАПо теореме 15.1 плоскость единственна, следовательно прямая b единственна.Теорема доказана.
- 6. признак параллельности прямых в пространстве.Если две
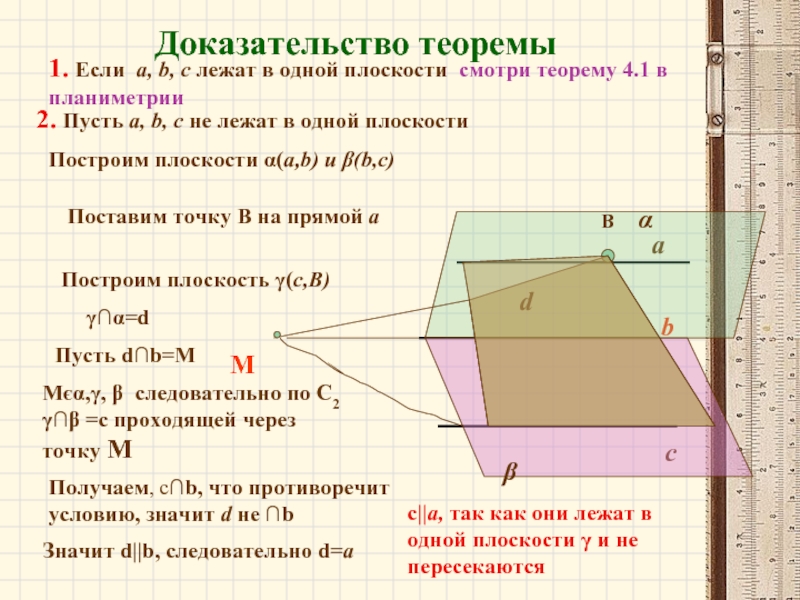
- 7. Доказательство теоремы1. Если a, b, c лежат
- 8. Скачать презентанцию
Параллельность в пространствеПараллельность прямыхПараллельность прямой и плоскостиПараллельность плоскостей
Слайды и текст этой презентации
Слайд 1параллельность прямых в
пространстве
Выполнила учитель математики МОУ Поназыревская средняя
школа Орлова Н.В.
Слайд 2Параллельность в пространстве
Параллельность прямых
Параллельность прямой и плоскости
Параллельность плоскостей
Слайд 4свойство параллельных
прямых в пространстве
Через точку вне данной прямой в
пространстве можно провести прямую параллельную данной и притом только одну.
Дано:
прямая а и точка А ¢ аДоказать : существует прямая b || a, b единственна
Теорема 16.1
Слайд 5Доказательство теоремы 16.1
а
А
По теореме 15.1 плоскость единственна, следовательно прямая b
единственна.
Теорема доказана.
Слайд 6признак параллельности
прямых в пространстве.
Если две прямые параллельны третьей прямой,
то они тоже параллельны
Дано: а||b; c||b
Доказать : a||c
Теорема 16.2
Слайд 7Доказательство теоремы
1. Если a, b, c лежат в одной плоскости
смотри теорему 4.1 в планиметрии
Mєα,γ, β следовательно по С2 γ∩β
=с проходящей через точку М Получаем, c∩b, что противоречит условию, значит d не ∩b
c||a, так как они лежат в одной плоскости γ и не пересекаются
Теги