Разделы презентаций
- Разное
- Английский язык
- Астрономия
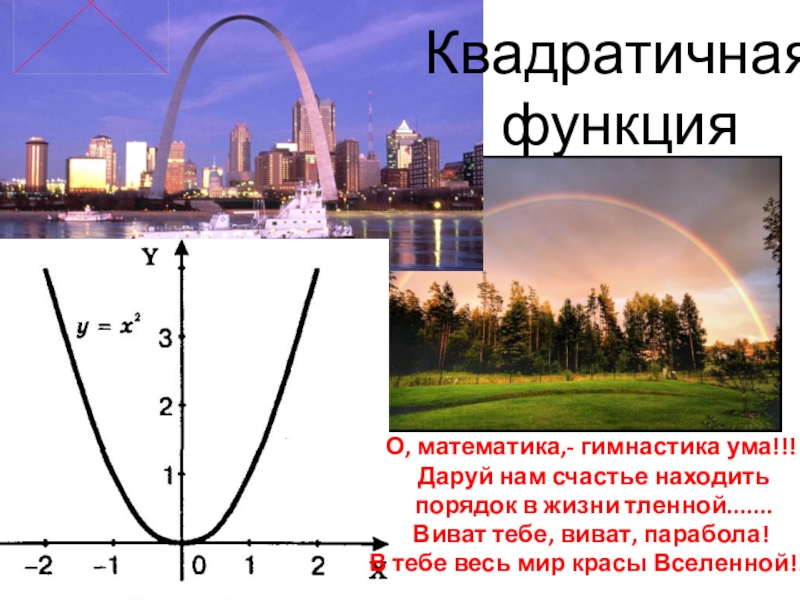
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельный перенос и Поворот
Содержание
- 1. Параллельный перенос и Поворот
- 2. Параллельный перенос и Поворот.
- 3. Содержание. Основные виды
- 4. Осевая и центральная симметрииПоворотПараллельный перенос Основные виды движений:
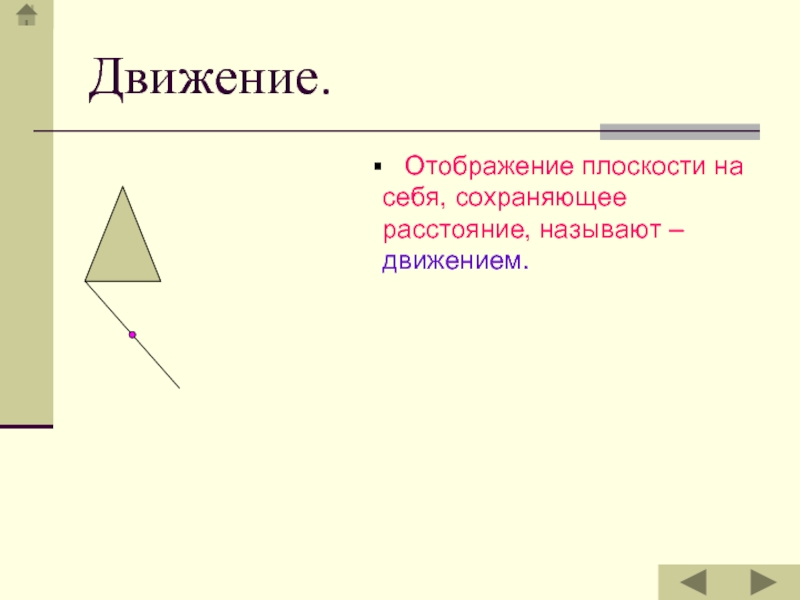
- 5. Отображение плоскости на себя, сохраняющее расстояние, называют – движением.Движение.
- 6. Поворотом фигуры F вокруг центра O на
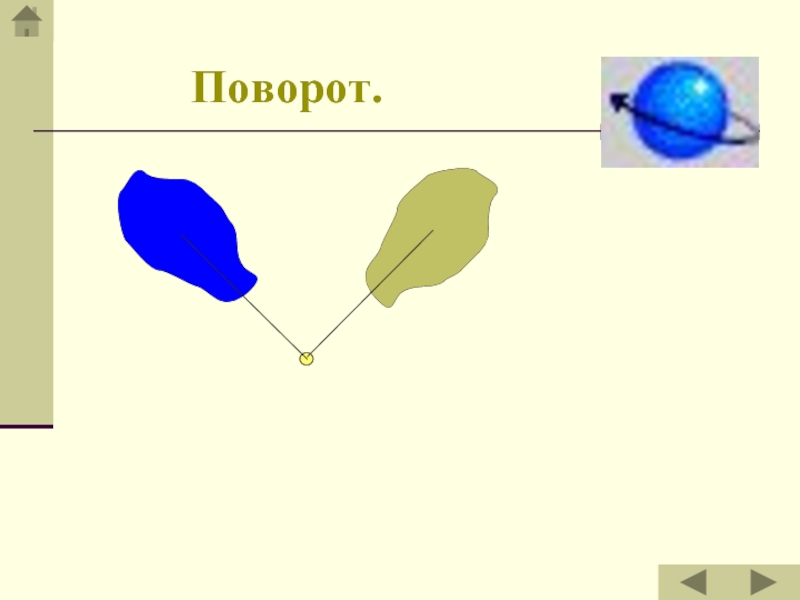
- 7. Поворот.
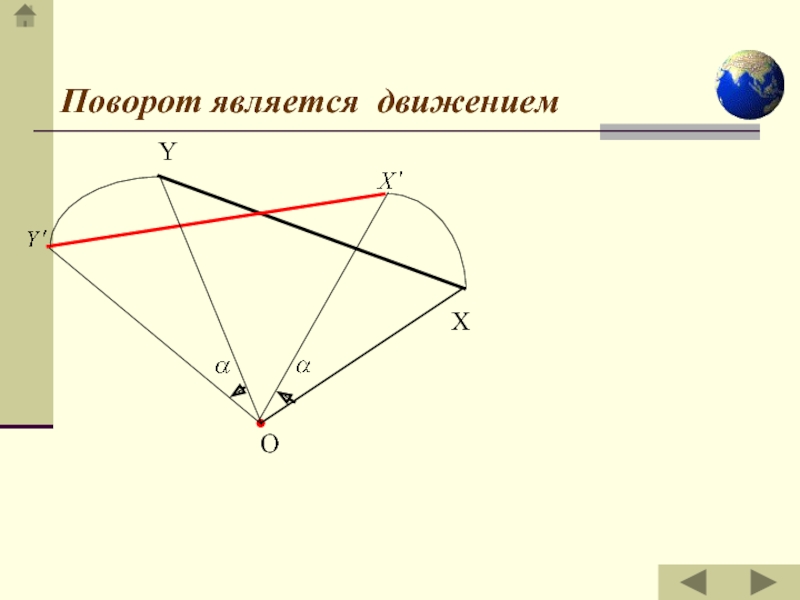
- 8. Поворот является движением ОYX
- 9. А(-4:-1)В(-5;3)D(-1;1)С(-1;3)A1(1;4)B1(3;5)C1(3;1)D1(1;1)Задача:Построить образ данной трапеции при повороте на 900 вокруг начала координат по часовой стрелке.
- 10. MNN1M1Центральная симметрия есть поворот на 180°:О
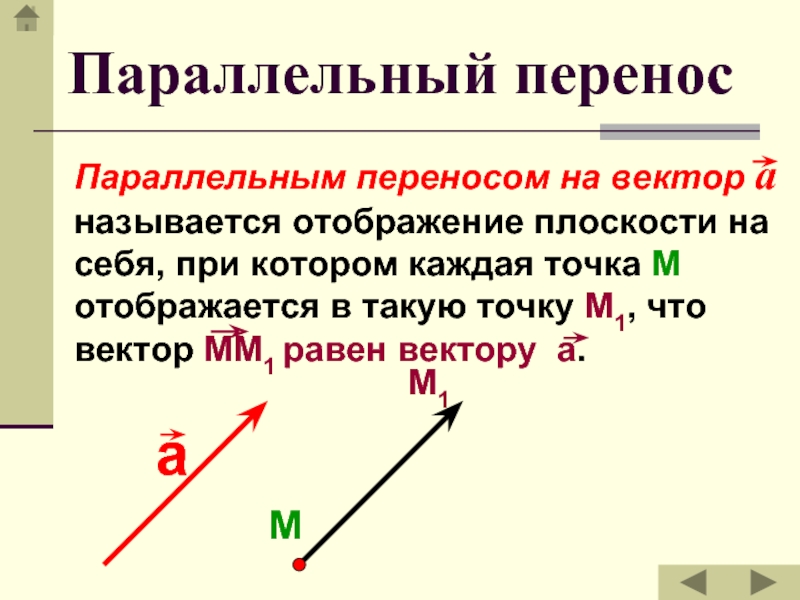
- 11. Параллельный перенос Параллельным переносом на вектор а
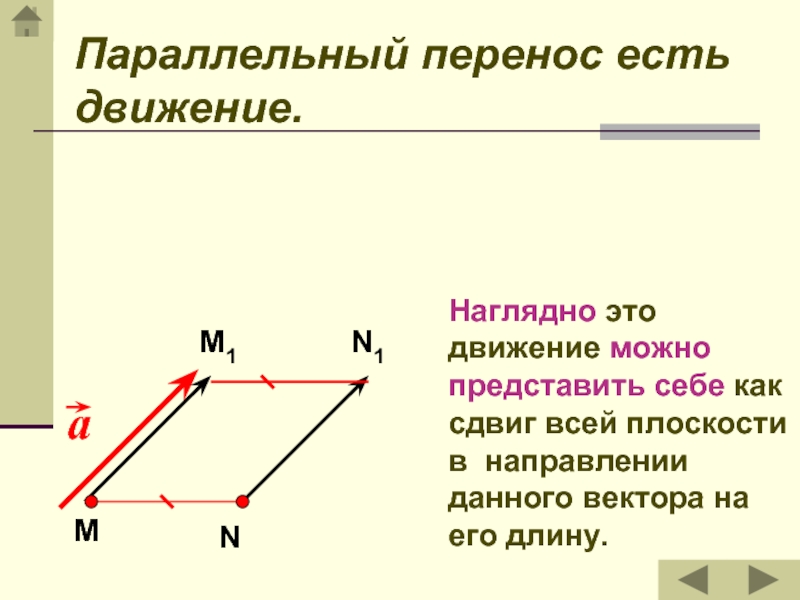
- 12. Параллельный перенос есть движение. Наглядно это движение
- 13. Параллельный перенос на плоскости в системе координат.Введем
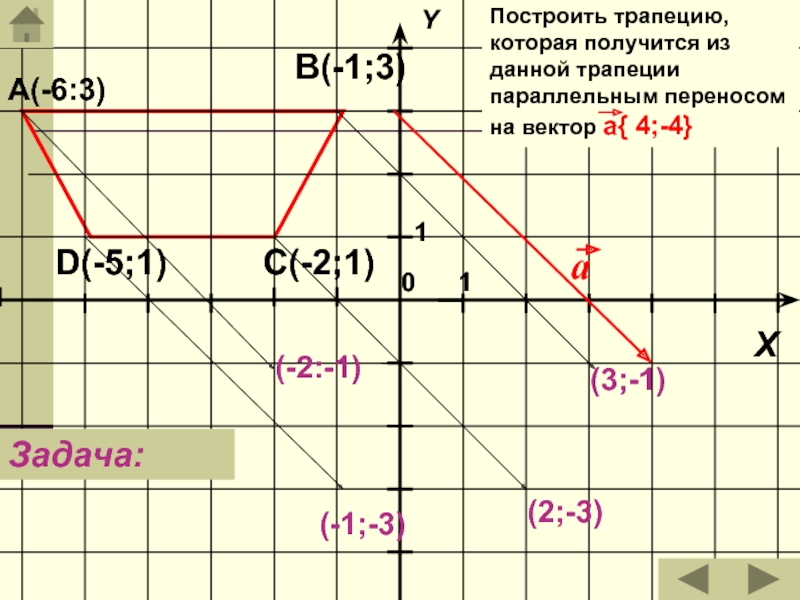
- 14. А(-6:3)В(-1;3)С(-2;1)D(-5;1)Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор a{ 4;-4}Задача:(-2:-1)(3;-1)(2;-3)(-1;-3)
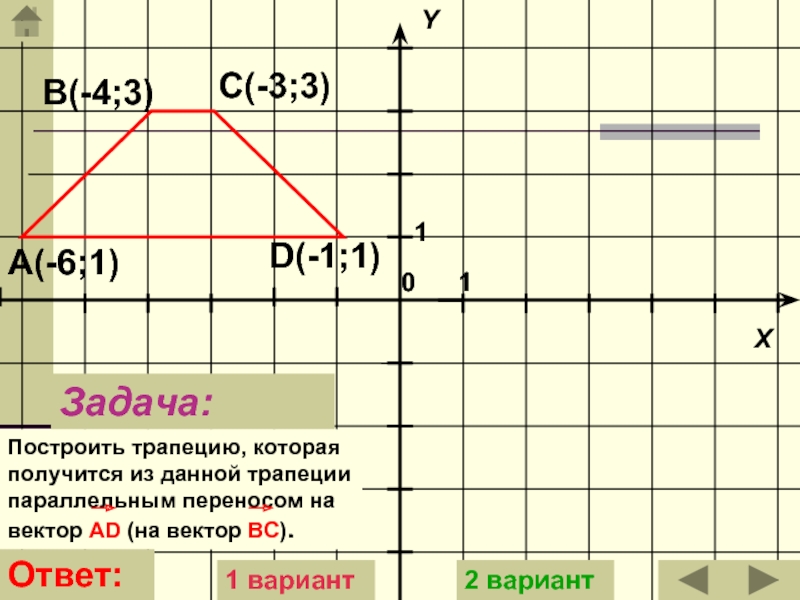
- 15. Задача:Построить трапецию, которая получится из данной трапеции
- 16. C1(2;3)D1(4;1)B1(1;3)A1(-1;1)1 вариант (ответ)2 вариант
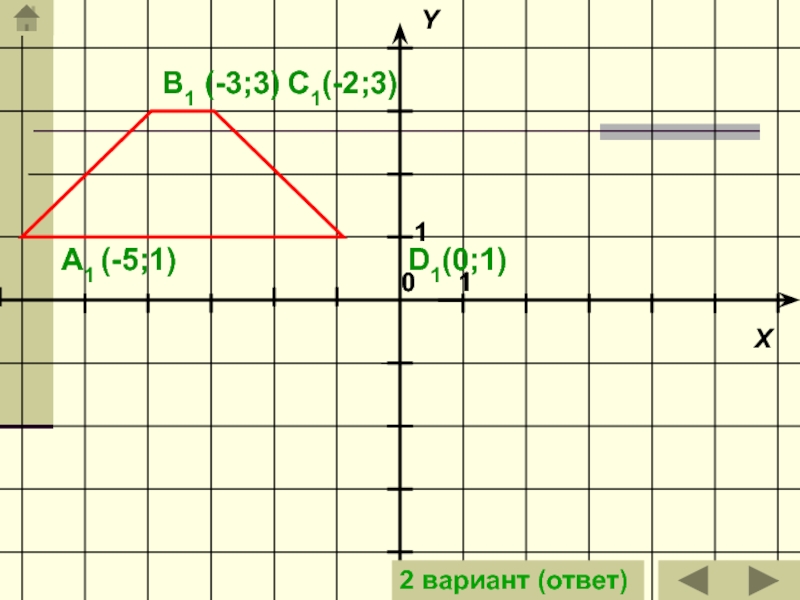
- 17. A1 (-5;1)B1 (-3;3)C1(-2;3)D1(0;1)2 вариант (ответ)
- 18. Спасибо за внимание.
- 19. Скачать презентанцию
Параллельный перенос и Поворот.
Слайды и текст этой презентации
Слайд 1Все права защищены. Полное или частичное копирование материалов без согласия
их владельца, запрещено!
АлексеевичаСлайд 6
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°)
в данном направлении называется такое ее преобразование, при котором каждой
точке X Є F сопоставляется точка X' так, чтоx'
Слайд 9
А(-4:-1)
В(-5;3)
D(-1;1)
С(-1;3)
A1(1;4)
B1(3;5)
C1(3;1)
D1(1;1)
Задача:
Построить образ данной трапеции при повороте на 900 вокруг начала
координат по часовой стрелке.
Слайд 11Параллельный перенос
Параллельным переносом на вектор а называется отображение плоскости
на себя, при котором каждая точка М отображается в такую
точку М1, что вектор ММ1 равен вектору а.М
М1
Слайд 12Параллельный перенос есть движение.
Наглядно это движение можно представить себе
как сдвиг всей плоскости в направлении данного вектора на его
длину.Слайд 13Параллельный перенос на плоскости в системе координат.
Введем на плоскости систему
координат O, X, Y. Преобразование фигуры F, при котором произвольная
ее точка M (x; y) переходит в точку M' (x+a;y+b) , где a и b – одни и те же для всех точек (x; y), называется параллельным переносом.
Слайд 14
А(-6:3)
В(-1;3)
С(-2;1)
D(-5;1)
Построить трапецию, которая получится из данной трапеции параллельным переносом на
вектор a{ 4;-4}
Задача:
(-2:-1)
(3;-1)
(2;-3)
(-1;-3)
Слайд 15
Задача:
Построить трапецию, которая получится из данной трапеции параллельным переносом на
вектор АD (на вектор BC).
А(-6;1)
В(-4;3)
С(-3;3)
D(-1;1)
Ответ:
1 вариант
2 вариант
Теги