Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность
Содержание
- 1. Перпендикулярность
- 2. План урокаНемного теорииПолезные упражненияСоставление плана решения задачРешение задач по готовым чертежамТест «Перпендикулярность»Итог урокаДомашнее задание
- 3. Немного теорииДайте понятие угла между двумя плоскостями.Сформулируйте
- 4. Полезные упражнения
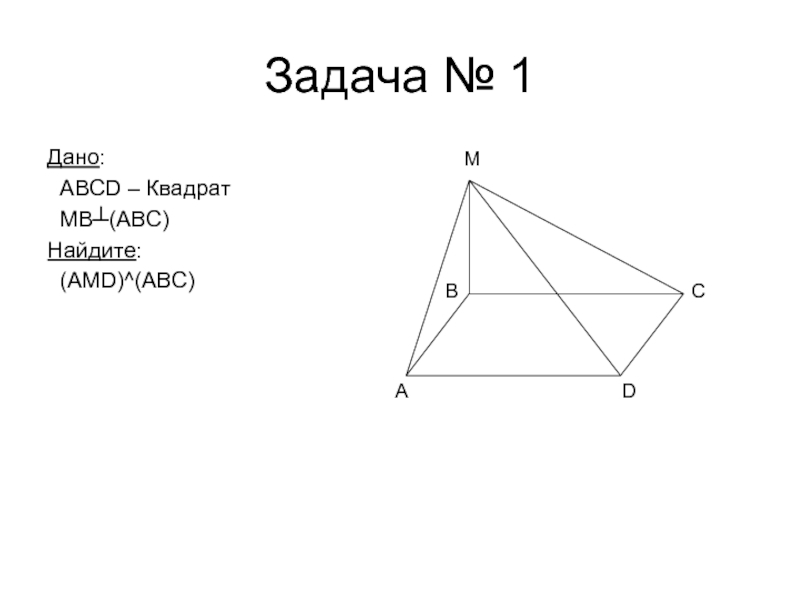
- 5. Задача № 1Дано: ABCD – Квадрат MB┴(ABC)Найдите: (AMD)^(ABC)ADCMB
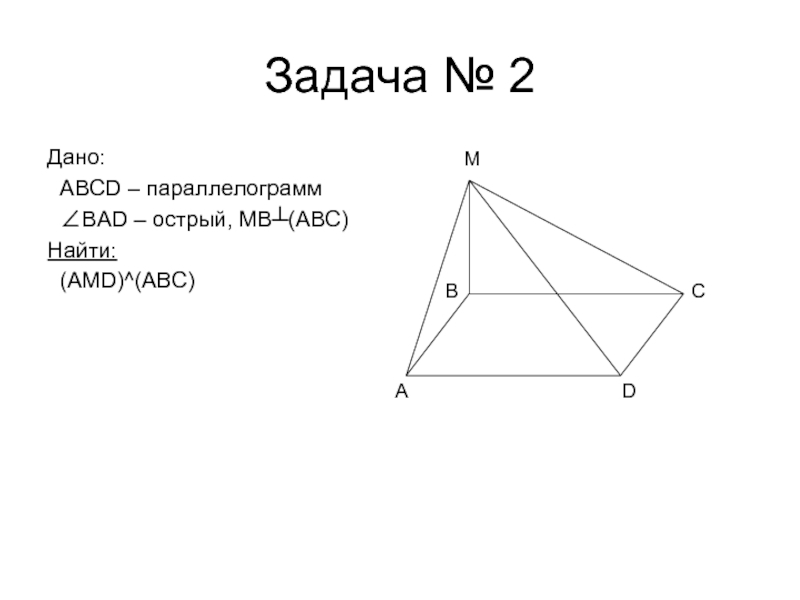
- 6. Задача № 2Дано: ABCD – параллелограмм ∠BAD – острый, MB┴(ABC)Найти: (AMD)^(ABC)ADCMB
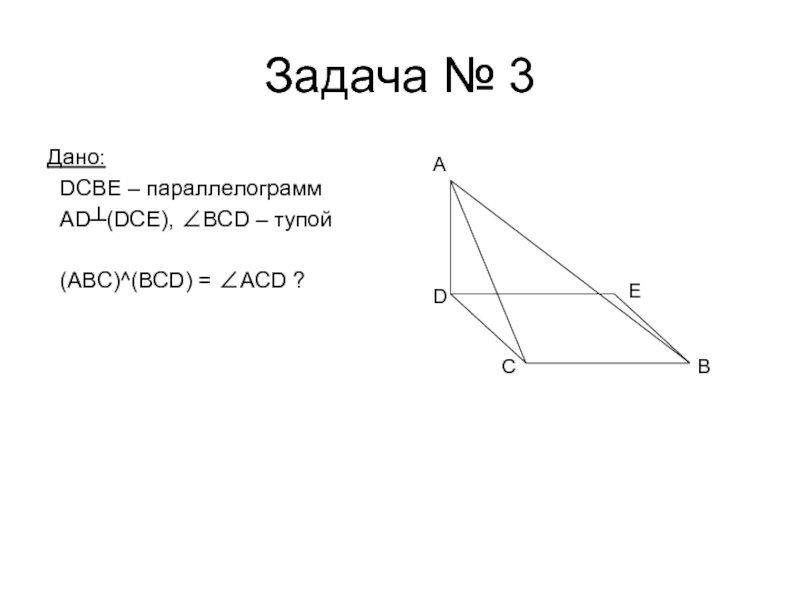
- 7. Задача № 3Дано: DCBE – параллелограмм AD┴(DCE), ∠BCD – тупой (ABC)^(BCD) = ∠ACD ?CADEB
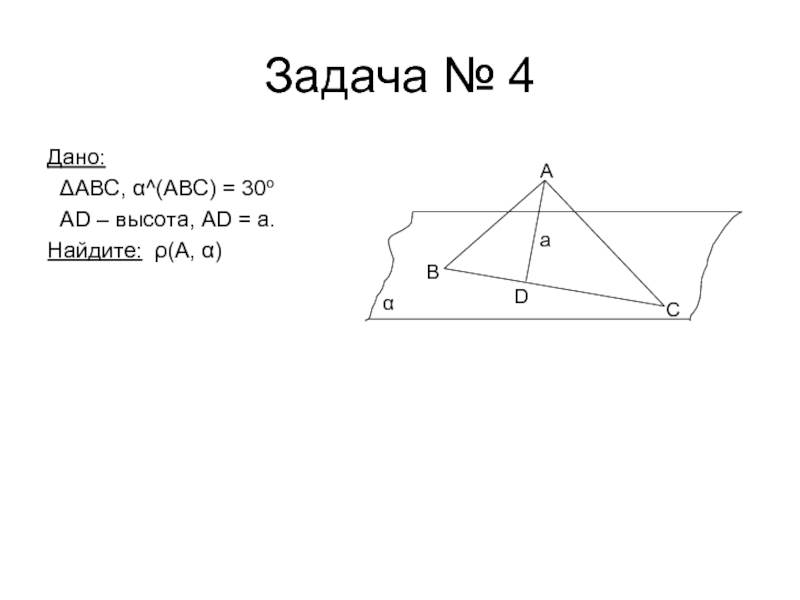
- 8. Задача № 4Дано: ΔABC, α^(ABC) = 30o AD – высота, AD = a.Найдите: ρ(А, α)АBDCaα
- 9. Задача № 5Дано: ΔABC, ∠C=90o α ^ (ABC)=30o BC = AC = aНайдите: ρ(А, α)BCAaaα
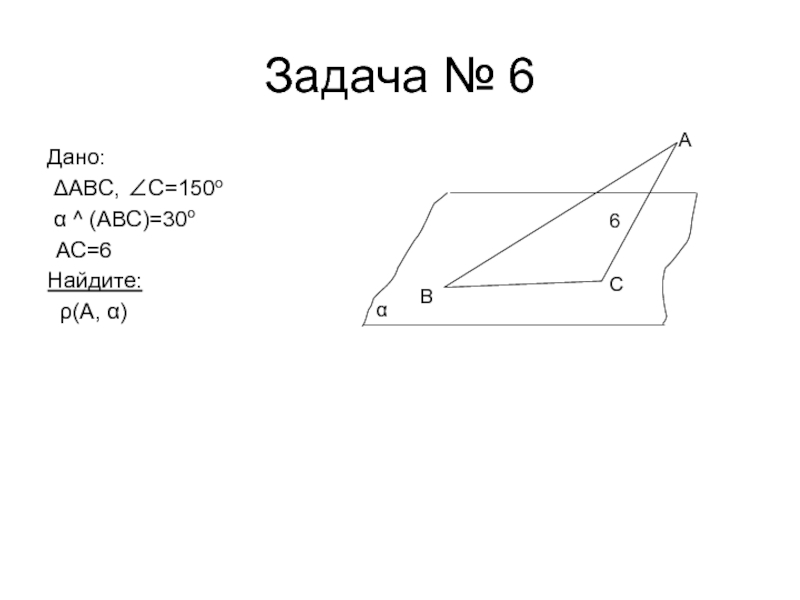
- 10. Задача № 6Дано: ΔABC, ∠C=150o α ^ (ABC)=30o АС=6Найдите: ρ(А, α)BCA6α
- 11. Задача № 7Верно ли, что:(SAB)^(DBC)=90o(SBC)┴(SAB)(SAC)┴(DBC)(SCD)^(DBC)=90o(DBC)┴(ASP)(SBC)^(ASP)=90oBCDSAP
- 12. Составление плана решения задач
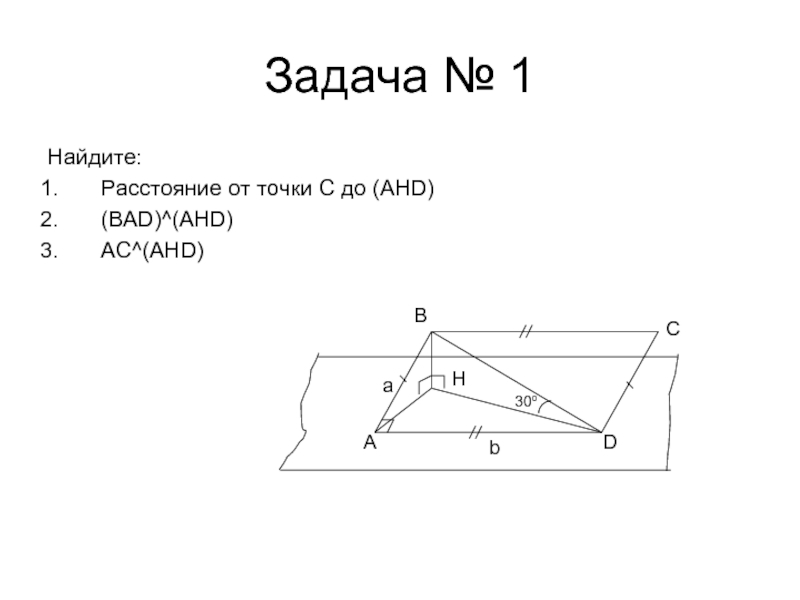
- 13. Задача № 1Найдите:Расстояние от точки C до (AHD)(BAD)^(AHD)AC^(AHD)ADCBHab30o
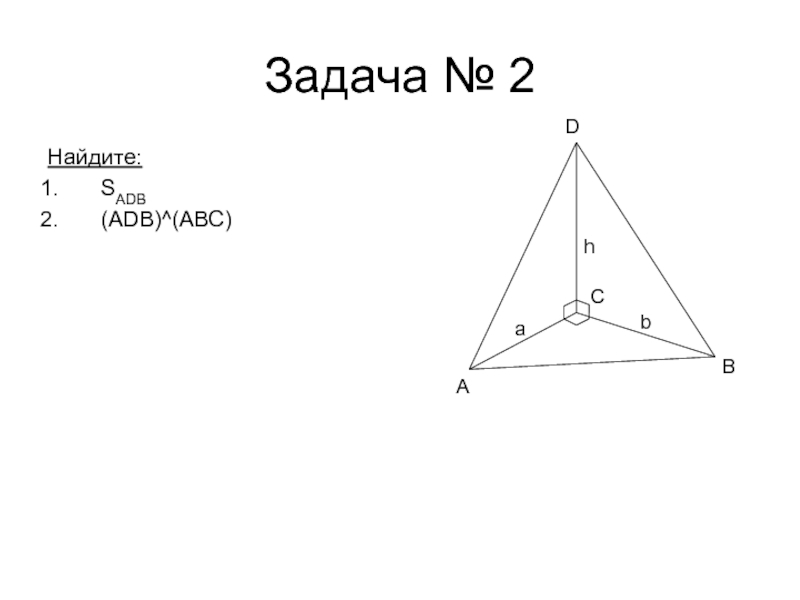
- 14. Задача № 2Найдите:SADB(ADB)^(ABC)ABDhaCb
- 15. Решение задач по готовым чертежам
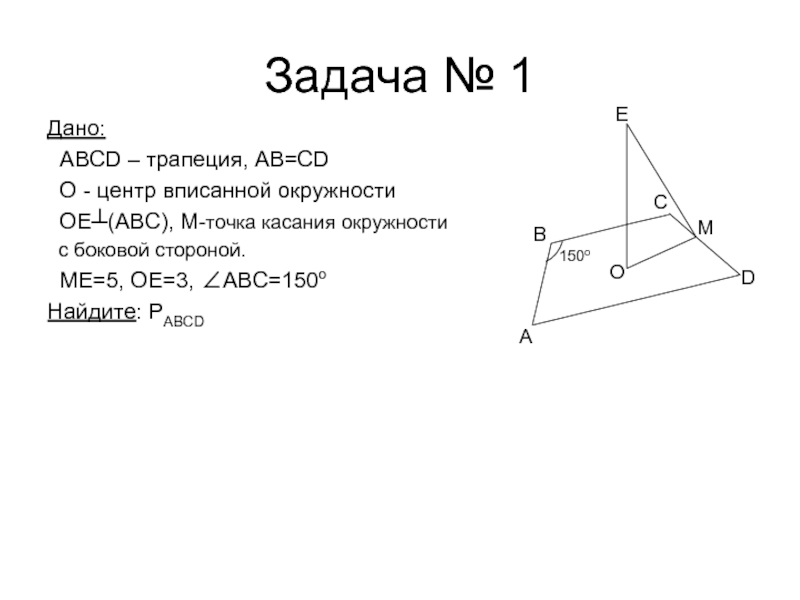
- 16. Задача № 1Дано: ABCD – трапеция,
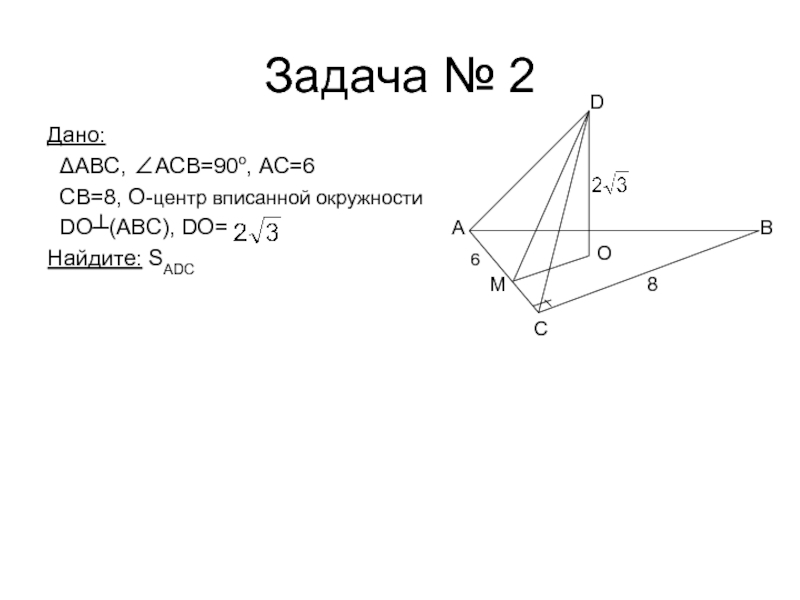
- 17. Задача № 2Дано: ΔABC, ∠АCВ=90o, AC=6 CB=8, O-центр вписанной окружности DO┴(ABC), DO=Найдите: SADC CBADMO86
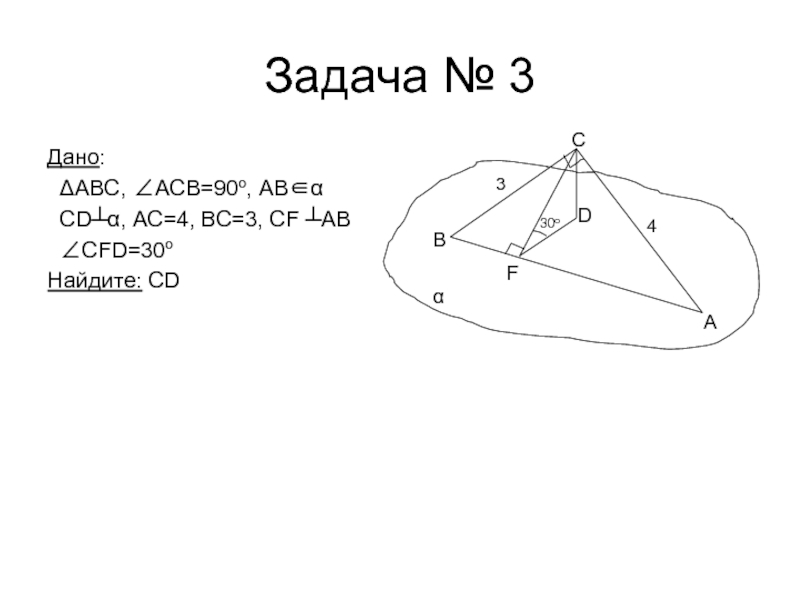
- 18. Задача № 3Дано: ΔABC, ∠АCВ=90o, AB∈α CD┴α, AC=4, BC=3, CF ┴AB ∠CFD=30oНайдите: CDFABDC34α30o
- 19. Тест «Перпендикулярность»
- 20. В-11.Какое из следующих утверждений верно?
- 21. 3. DАВС – правильная треугольная пирамида. DО
- 22. В-21.Какое из следующих утверждений верно?
- 23. 3. DАВС – треугольная пирамида. DВ –
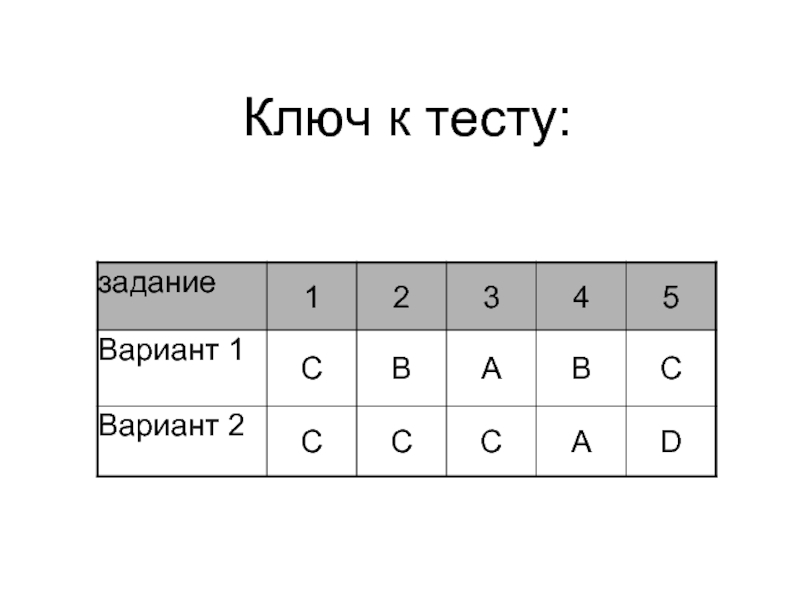
- 24. Ключ к тесту:
- 25. Итоги урока
- 26. Оценки за урок:
- 27. Домашнее заданиеВ равнобедренном треугольнике основание и высота
- 28. Скачать презентанцию
План урокаНемного теорииПолезные упражненияСоставление плана решения задачРешение задач по готовым чертежамТест «Перпендикулярность»Итог урокаДомашнее задание
Слайды и текст этой презентации
Слайд 2План урока
Немного теории
Полезные упражнения
Составление плана решения задач
Решение задач по готовым
чертежам
Слайд 3Немного теории
Дайте понятие угла между двумя плоскостями.
Сформулируйте определение перпендикулярности двух
плоскостей.
Сформулируйте признак перпендикулярности двух плоскостей.
Какая фигура называется двугранным углом? Линейным
углом двугранного угла?Каково взаимное расположение граней двугранного угла и плоскости двугранного угла?
Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла?
Можно ли утверждать, что две плоскости перпендикулярные третьей параллельны?
Верно- ли , что прямая и плоскость перпендикулярные другой плоскости, параллельны между собой?
Где лежит высота тупоугольного треугольника, проведенная из вершины острого угла?
В какую трапецию можно вписать окружность?
Свойство касательной и радиуса, проведенного в точку касания.
Свойство высоты прямоугольного треугольника, проведенной к гипотенузе.
Слайд 11Задача № 7
Верно ли, что:
(SAB)^(DBC)=90o
(SBC)┴(SAB)
(SAC)┴(DBC)
(SCD)^(DBC)=90o
(DBC)┴(ASP)
(SBC)^(ASP)=90o
B
C
D
S
A
P
Слайд 16Задача № 1
Дано:
ABCD – трапеция, AB=CD
О -
центр вписанной окружности
ОЕ┴(ABC), М-точка касания окружности
с боковой стороной.
ME=5, OE=3, ∠ABC=150oНайдите: PABCD
A
D
M
O
B
C
E
150o
Слайд 17Задача № 2
Дано:
ΔABC, ∠АCВ=90o, AC=6
CB=8, O-центр вписанной
окружности
DO┴(ABC), DO=
Найдите: SADC
C
B
A
D
M
O
8
6
Слайд 18Задача № 3
Дано:
ΔABC, ∠АCВ=90o, AB∈α
CD┴α, AC=4, BC=3,
CF ┴AB
∠CFD=30o
Найдите: CD
F
A
B
D
C
3
4
α
30o
Слайд 20В-1
1.Какое из следующих утверждений верно?
А: двугранным углом называется фигура, образованная прямой а и двумя
полуплоскостями с общей границей а;В: двугранный угол имеет бесконечное множество различных линейных углов;
С: градусной мерой двугранного угла называется градусная мера его линейного угла;
D: угол между пересекающимися плоскостями может быть тупым;
2. При пересечении двух плоскостей образовались двугранные углы, один из которых в два раза больше другого. Найдите градусную меру угла между плоскостями.
А: 300; В: 600; С:900; D: 1200.
Слайд 213. DАВС – правильная треугольная пирамида. DО – высота пирамиды,
а точка Е – середина стороны ВС. Линейным углом двугранного
угла DВСО являетсяА: DЕО; В: DВО; С: DЕВ; D: угол не обозначен.
4. АВСDА1В1С1D1 - прямоугольный параллелепипед, О – точка пересечения диагоналей грани АВСD. Расстояние от точки С1 до диагонали ВD равно
А: С1С; В: С1О; С: С1В; D:С1D.
5. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости, а катет наклонен к этой плоскости под углом 300. найдите угол между плоскостью и плоскостью треугольника.
А: 900; В: 600; С:450; D: 300.
Слайд 22 В-2
1.Какое из следующих утверждений верно?
А: градусная мера двугранного угла не превосходит 900;
В: двугранным углом называется угол, образованный прямой а и двумя полуплоскостями с общей границей а;С: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны;
D: угол между плоскостями тупой.
2. При пересечении двух плоскостей образовались двугранные углы, градусная мера одного из которых на 300 больше градусной меры другого. Найдите градусную меру угла между этими плоскостями.
А: 1050; В: 900; С:750; D: 600
Слайд 233. DАВС – треугольная пирамида. DВ – высота пирамиды, а
точка Е – середина стороны АС. Линейным углом двугранного угла
АВDС являетсяА: DВА; В: DВЕ; С: АВС; D: угол не обозначен.
4. АВСDА1В1С1D1 - прямоугольная призма, Точка О1 и О –пересечения диагоналей оснований АВСD и А1В1С1D. Расстояние от точки С1 до диагонали АС равно
А: С1С; В: С1А; С: С1О; D:С1О.
5. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости угол между плоскостью и плоскостью треугольника равен 450. Найдите градусную меру угла, под которым катет наклонен к плоскости.
А: 900; В: 600; С:450; D: 300
Слайд 27Домашнее задание
В равнобедренном треугольнике основание и высота равны по 4.
Данная точка находится на расстоянии 6 от плоскости треугольника и
на равном расстоянии от его вершин. Найдите это расстояние.Катеты прямоугольного треугольника АВС равны 3 и 4. Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр CD = 1. Найдите расстояние от точки D до гипотенузы АВ.
Стороны треугольника относятся как 10 : 17 : 21, а его площадь равна 84. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15. Найдите расстояние от его концов до большей стороны.
В треугольнике АВС угол С прямой; CD – перпендикуляр к плоскости этого треугольника. Точка D соединена с А и В. Найдите площадь треугольника ADB, если : СА = 3, ВС = 2 и CD = 1.
Теги