Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подобие в геометрии. Подобные треугольники
Содержание
- 1. Подобие в геометрии. Подобные треугольники
- 2. ТЕМА «ПОДОБИЕ»Теоретический материал.Задачи.
- 3. ПЛАНПропорциональные отрезки.Свойство биссектрисы треугольника.Определение подобных треугольников.Отношение периметров подобных фигур.Отношение площадей подобных фигур.Признаки подобия треугольников.
- 4. ЗАДАЧИРазминка.Решение задач.Задачи на признаки подобия.Тест
- 5. Пропорциональные отрезкиОтношением отрезков называется отношение их длин.Отрезки
- 6. ПРИМЕРДаны два прямоугольных треугольникаСтороны ΒC и CA
- 7. Пропорциональность отрезковПонятие пропорциональности вводится для любого числа отрезков.например
- 8. Подобные фигурыПредметы одинаковой формы, но разных размеровФотографии,
- 9. Подобные фигурыВ геометрии фигуры одинаковой формы называют
- 10. Подобные треугольникиДаны два треугольника AΒC и A1Β1C1,у
- 11. ОпределениеДва треугольника называются подобными, если их углы
- 12. Коэффициент подобияЧисло k , равное отношению сходственных сторон, называется коэффициентом подобия.ΔAΒC ~ ΔA1Β1C1k – коэффициент подобия.
- 13. Дополнительные свойстваОтношение высот подобных треугольников, проведенных к
- 14. Отношение периметровОтношение периметров подобных треугольников равно коэффициенту подобия.ΔAΒC ~ ΔA1Β1C1ДОКАЗАТЕЛЬСТВО
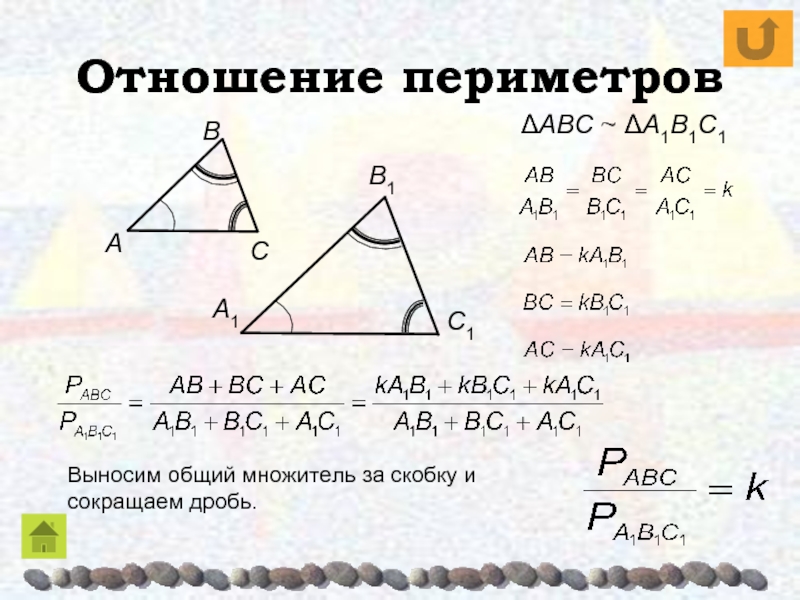
- 15. Отношение периметровВыносим общий множитель за скобку и сокращаем дробь.
- 16. Отношение площадейОтношение площадей подобных треугольников равно квадрату коэффициента подобия.ΔAΒC ~ ΔA1Β1C1ДОКАЗАТЕЛЬСТВО
- 17. Отношение площадейПусть ΔAΒC ~ ΔA1Β1C1, коэффициент подобия
- 18. Свойство биссектрисы треугольникаC BAБиссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.DилиДОКАЗАТЕЛЬСТВОПРИМЕР
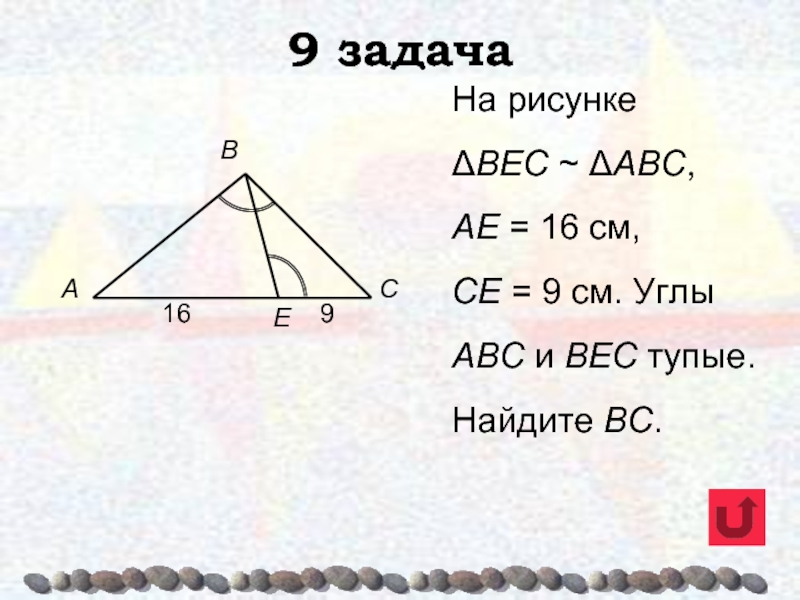
- 19. Свойство биссектрисы треугольникаΔABD и ΔACD имеют общую
- 20. Свойство биссектрисы треугольникаДано: ΔABC AD – биссектрисаAB
- 21. Свойство биссектрисы треугольникаРешение:Пусть BD = x см,
- 22. Признаки подобия треугольниковПервый признак подобия треугольников.(по двум
- 23. Первый признак подобия треугольников.Если два угла одного
- 24. Первый признак подобия треугольников.Дано:ΔABC и ΔA1B1C1, ∠A =∠A1,∠B = ∠B.Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 25. Первый признак подобия треугольников.Доказательство: ∠A =
- 26. Первый признак подобия треугольников.Доказательство: ∠A =
- 27. Второй признак подобия треугольников. Если две стороны
- 28. Второй признак подобия треугольников. Дано:ΔABC и ΔA1B1C1, ∠A =∠A1,Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 29. Доказательство:Достаточно доказать, что ∠B = ∠B1.ΔABC2, ∠1=∠A1,
- 30. Третий признак подобия треугольников. Если три стороны
- 31. Третий признак подобия треугольников. Дано:ΔABC и ΔA1B1C1, Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 32. Третий признак подобия треугольников. Доказательство:Достаточно доказать, что
- 33. Разминка1Отрезки AB и CD пропорциональны отрезкам MN
- 34. Разминка2Даны два подобных прямоугольных треугольника. Коэффициент подобия
- 35. Разминка3По данным на рисунке найдите х.х = 15
- 36. Разминка4Длины двух окружностей 2π и 8π. Найдите
- 37. Разминка5Отношение площадей двух квадратов равно 9 :
- 38. Решение задач171348111514523129610
- 39. 1 задачаОтрезки AB и CD пропорциональны отрезкам
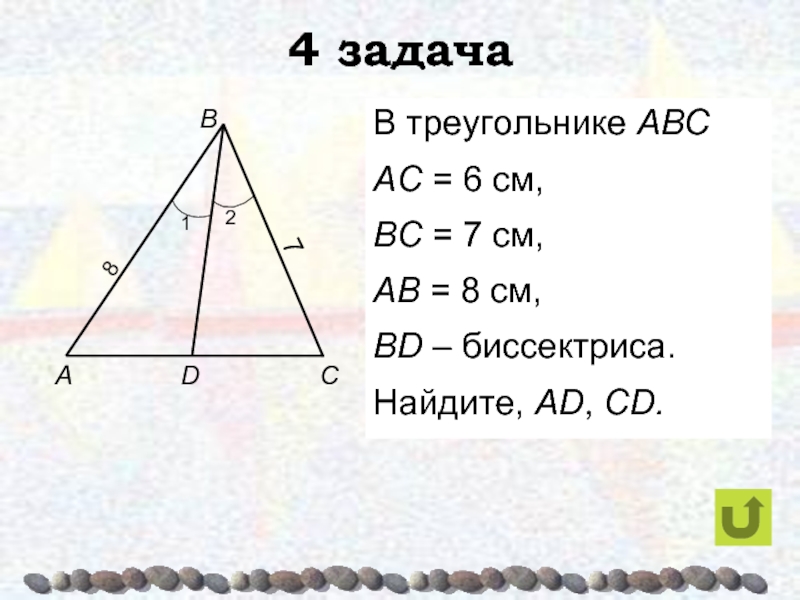
- 40. 4 задачаВ треугольнике АВСАС = 6 см,
- 41. 7 задачаТреугольник со сторонами 2 см, 3
- 42. 10 задачаСходственные стороны подобных треугольников относятся как
- 43. 13 задачаΔABC ~ ΔA1B1C1 , AB :
- 44. 2 задачаВ параллелограмме ABCD диагонали пересекаются в
- 45. 5 задачаОснование равнобедренного треугольника равно 18 мм,а
- 46. 8 задачаТреугольники KPF и ЕМТ подобны, причем
- 47. 11 задачаПериметры подобных треугольников 12 мм и
- 48. 14 задачаПлощади двух подобных треугольников равны 16
- 49. В треугольнике ABC точка K лежит на
- 50. 6 задачаAD = 4BC = 5AB + DC = 12 Найти AB, DC, AC
- 51. 9 задачаНа рисункеΔВЕС ~ ΔАВС, АЕ =
- 52. 12 задачаМасштаб плана 1 : 1000.Какова длина
- 53. 15 задачаПериметры подобных треугольников относятся как 2
- 54. ЗАДАЧИ1.Диагонали трапеции ABCD пересекаются в точке O.
- 55. РешениеРассмотрим ΔAOD и ΔBOC: ∠1=∠2 (накрест
- 56. Решение
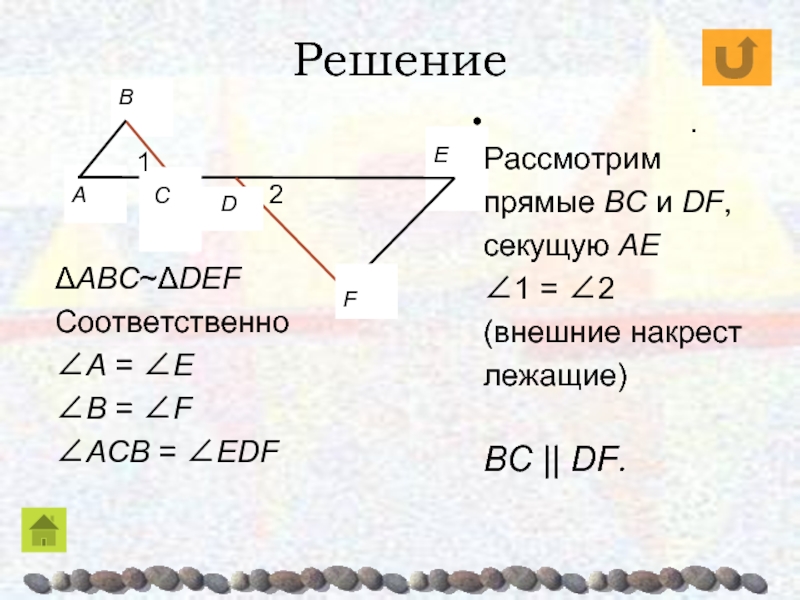
- 57. ЗАДАЧИ2.Докажите, что треугольники, изображенные на рисунке, подобны, и выясните взаимное положение прямых CB и DF.Решение:
- 58. РешениеОтсюда ΔABC~ΔDEF по трем пропорциональным сторонамНайдем отношение сходственных сторон данных треугольников
- 59. РешениеΔABC~ΔDEF Соответственно∠A = ∠E∠B = ∠F∠ACB =
- 60. ЗАДАЧИ3.Отрезки AB и CD пересекаются в точке
- 61. РешениеРассмотрим ΔAOD и ΔCOB∠DOA = ∠COB (вертикальные).
- 62. ЗАДАЧИ4. В треугольнике
- 63. Решение
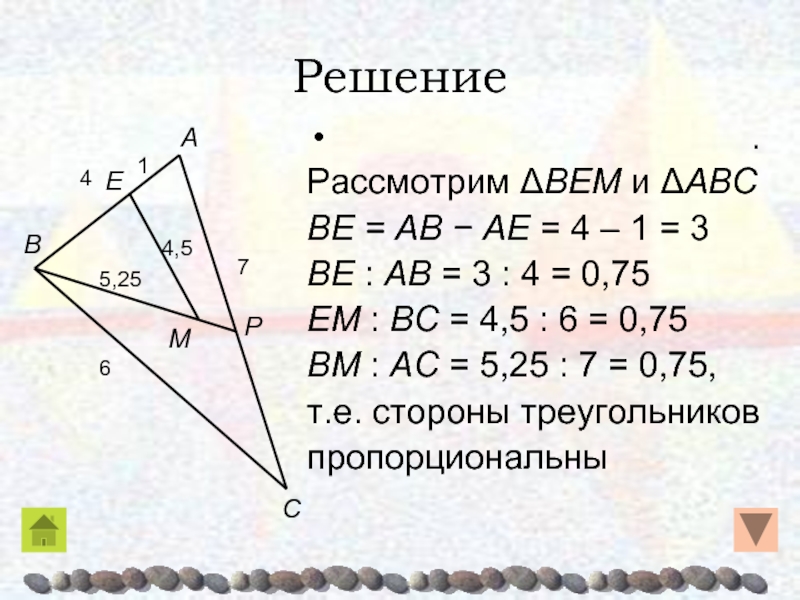
- 64. ΔBEM ~ ΔABC по трем пропорциональным
- 65. ЗАДАЧИ5.Диагональ AC параллелограмма ABCD равна 90. Середина
- 66. Рассмотрим ΔAOM и ΔCОD ∠AOM = ∠CОD
- 67. РешениеCΔAOM ~ ΔCОD
- 68. ТЕСТРешите задачи, отметьте нужные ячейки
- 69. ТЕСТ1. По данным рисунка х равенА) 7Б) 14В) 3,5Г) 14/3
- 70. ТЕСТ2) По данным рисунка периметр ΔABC равенА) 9Б) 27В) 36Г) 18
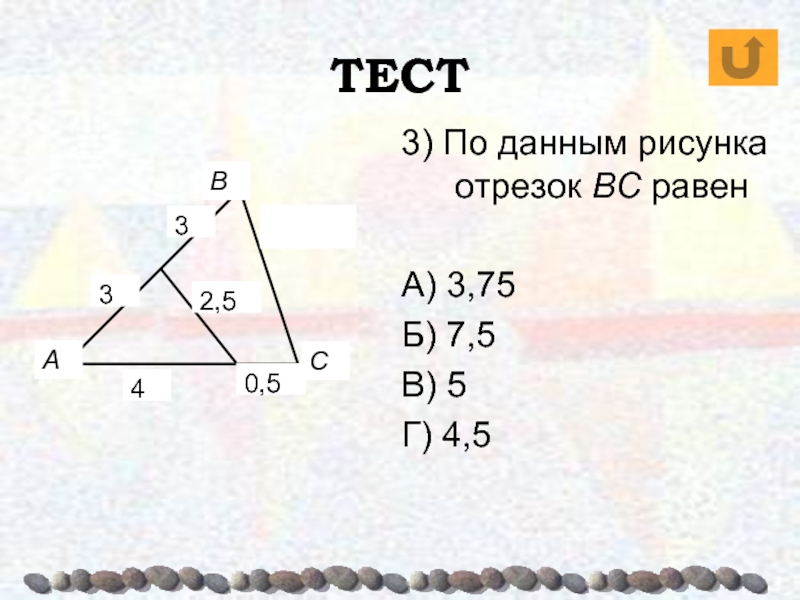
- 71. ТЕСТАВС3) По данным рисунка отрезок BC равенА) 3,75Б) 7,5В) 5Г) 4,53340,52,5
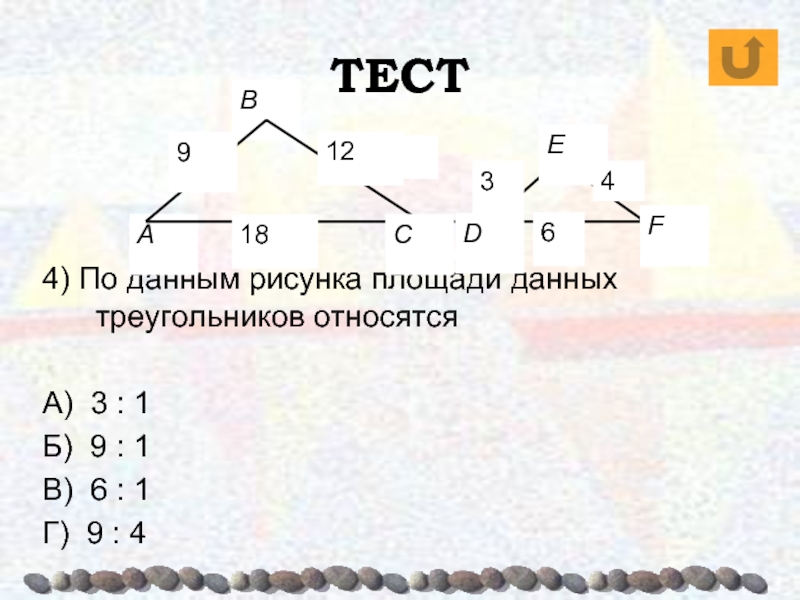
- 72. ТЕСТ4) По данным рисунка площади данных треугольников
- 73. ТЕСТ5) По данным рисунка прямые AB и DEА) нельзя ответитьБ) пересекаютсяВ) параллельны
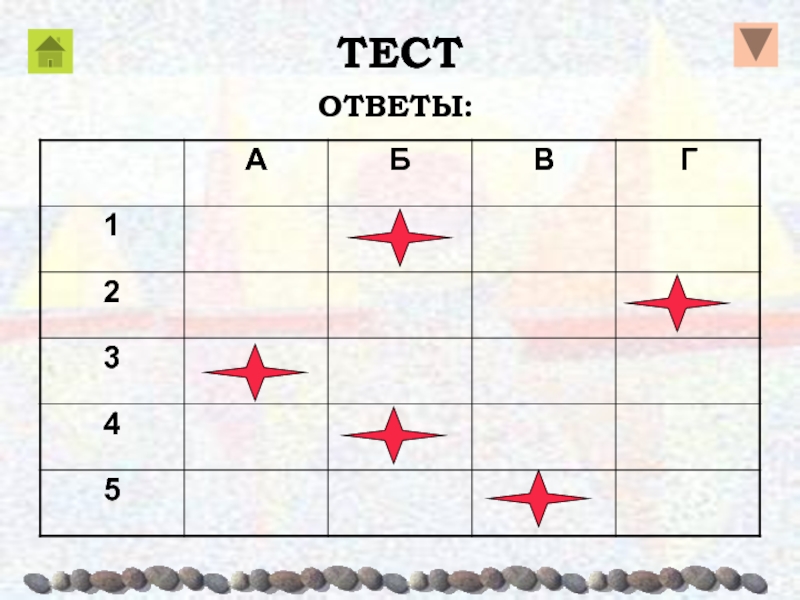
- 74. ТЕСТОТВЕТЫ:
- 75. Помощь в управлении презентациейуправление презентацией осуществляется
- 76. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3ПЛАН
Пропорциональные отрезки.
Свойство биссектрисы треугольника.
Определение подобных треугольников.
Отношение периметров подобных фигур.
Отношение площадей
подобных фигур.
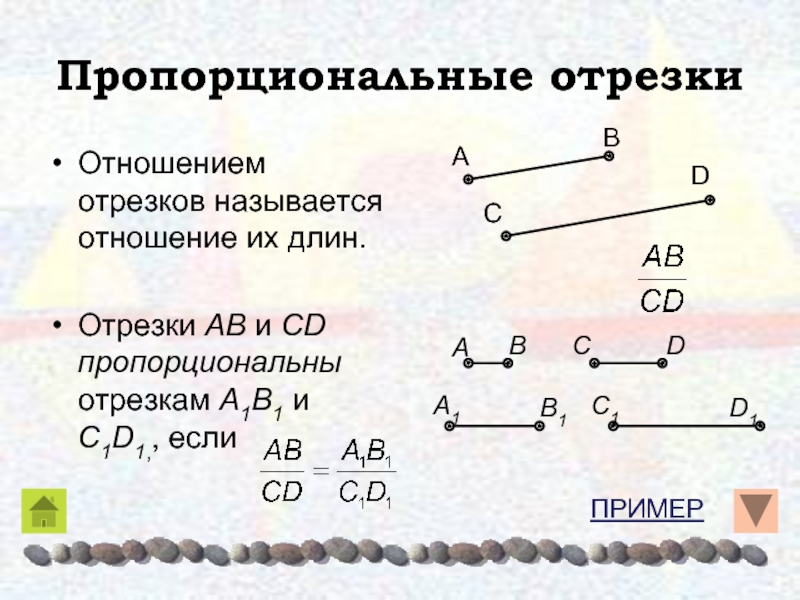
Слайд 5Пропорциональные отрезки
Отношением отрезков называется отношение их длин.
Отрезки AB и CD
пропорциональны отрезкам A1B1 и C1D1,, если
ПРИМЕР
Слайд 6ПРИМЕР
Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и
MK, так как
т.е.
и
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО ТРЕУГОЛЬНИКА.
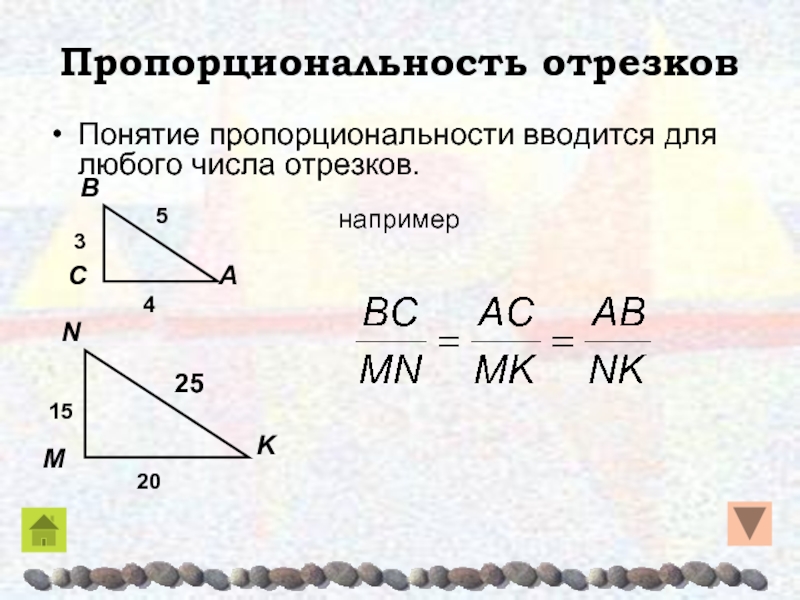
Слайд 7Пропорциональность отрезков
Понятие пропорциональности вводится для любого числа отрезков.
например
Слайд 8Подобные фигуры
Предметы одинаковой формы, но разных размеров
Фотографии, отпечатанные с одного
негатива, но с разными увеличениями;
Здание и его макет
Планы, географические карты одного и того же района, выполненные в разных масштабах.
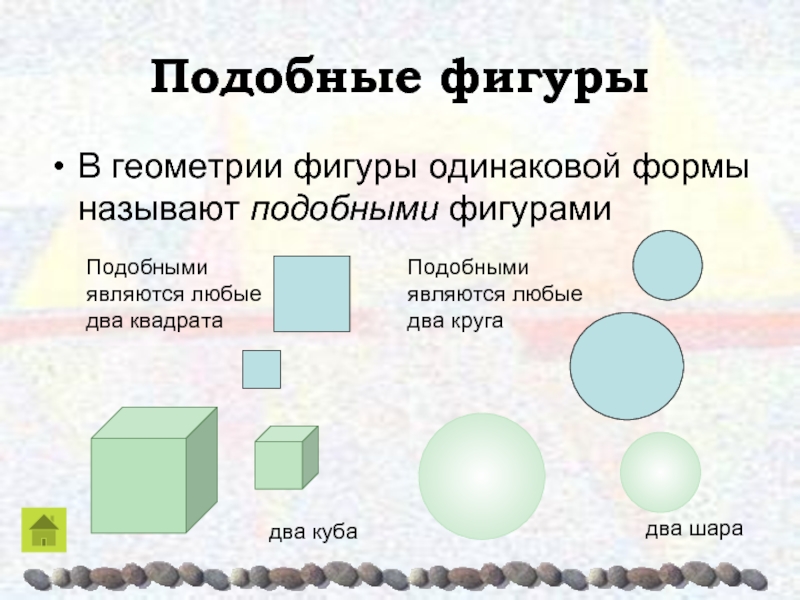
Слайд 9Подобные фигуры
В геометрии фигуры одинаковой формы называют подобными фигурами
Подобными являются
любые два квадрата
Подобными являются любые два круга
два куба
два шара
Слайд 10Подобные треугольники
Даны два треугольника AΒC и A1Β1C1,
у которых ∠A =
∠A1, ∠Β = ∠Β1, ∠C = ∠C1.
Стороны AΒ и A1Β1
, AC и A1C1 , ΒC и Β1C1, лежащие против равных углов, называют сходственными
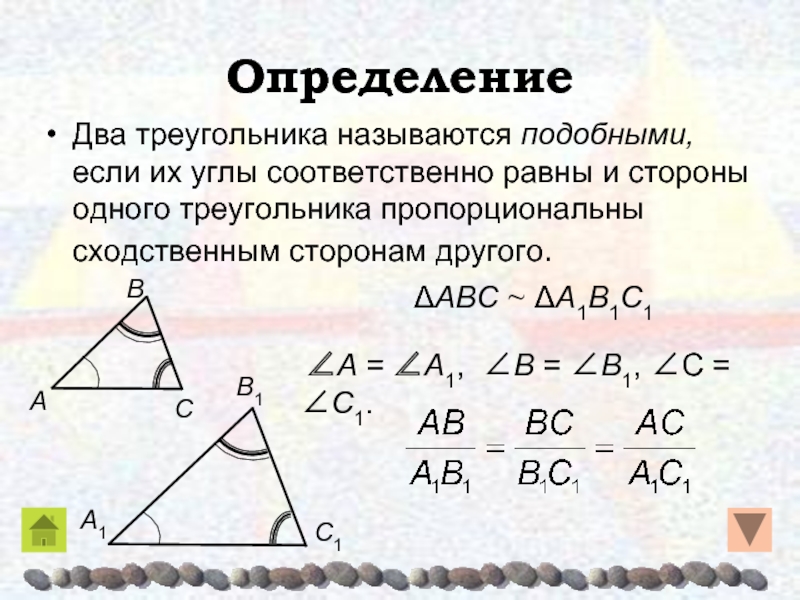
Слайд 11Определение
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
∠A = ∠A1,
∠Β = ∠Β1, ∠C = ∠C1.ΔAΒC ~ ΔA1Β1C1
Слайд 12Коэффициент подобия
Число k , равное отношению сходственных сторон, называется коэффициентом
подобия.
ΔAΒC ~ ΔA1Β1C1
k – коэффициент подобия.
Слайд 13Дополнительные свойства
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение медиан подобных треугольников, проведенных к сходственным сторонам, равно
коэффициенту подобия. Отношение биссектрис подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
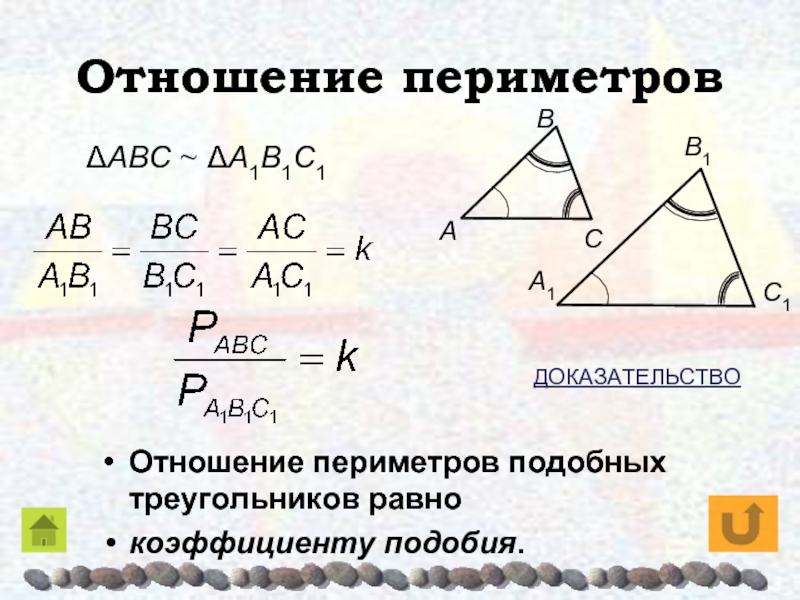
Слайд 14Отношение периметров
Отношение периметров подобных треугольников равно
коэффициенту подобия.
ΔAΒC ~ ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
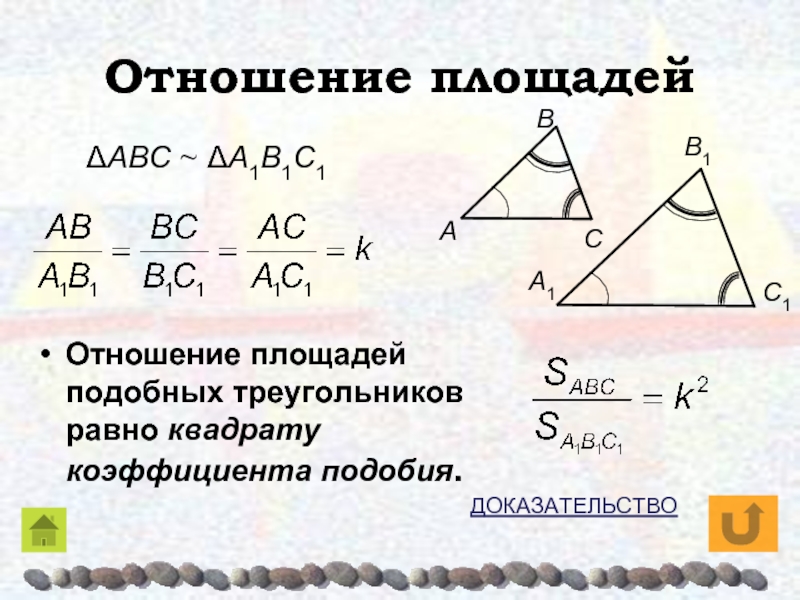
Слайд 16Отношение площадей
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
ΔAΒC ~
ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
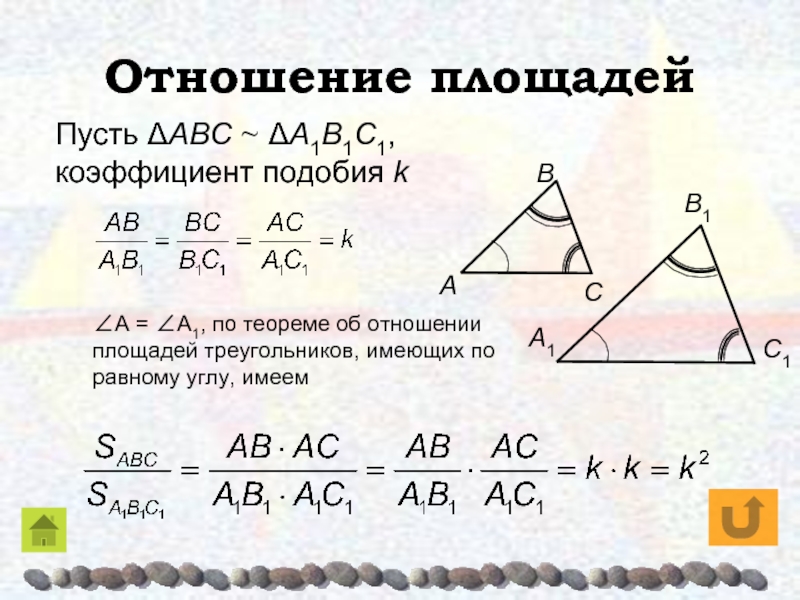
Слайд 17Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,
коэффициент подобия k
∠A = ∠A1,
по теореме об отношении площадей треугольников, имеющих по равному углу,
имеем
Слайд 18Свойство биссектрисы треугольника
C
B
A
Биссектриса треугольника делит противоположную сторону на отрезки,
пропорциональные прилежащим сторонам треугольника.
D
или
ДОКАЗАТЕЛЬСТВО
ПРИМЕР
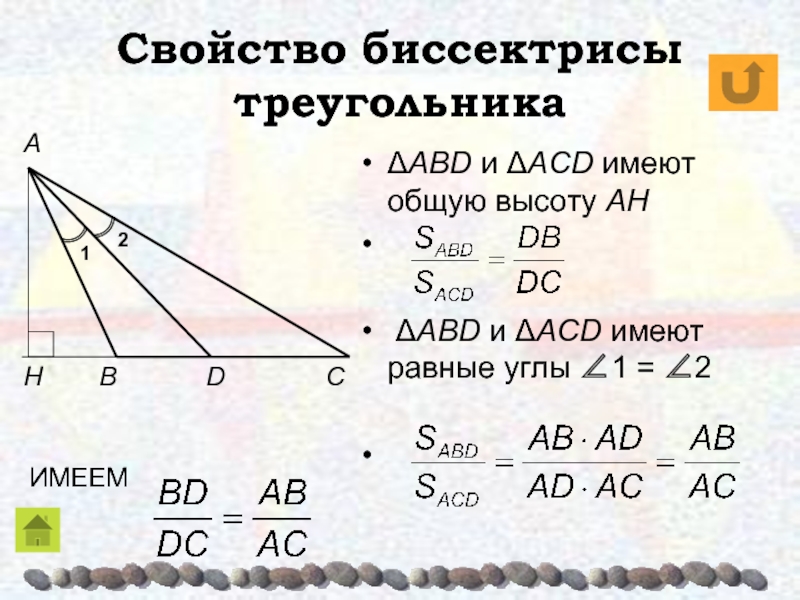
Слайд 19Свойство биссектрисы треугольника
ΔABD и ΔACD имеют общую высоту AH
ΔABD и ΔACD имеют равные углы ∠1 = ∠2
ИМЕЕМ
Слайд 20Свойство биссектрисы треугольника
Дано: ΔABC
AD – биссектриса
AB = 14 см
BC
= 20 см
AC = 21 см
Найти: BD,CD.
Решение:
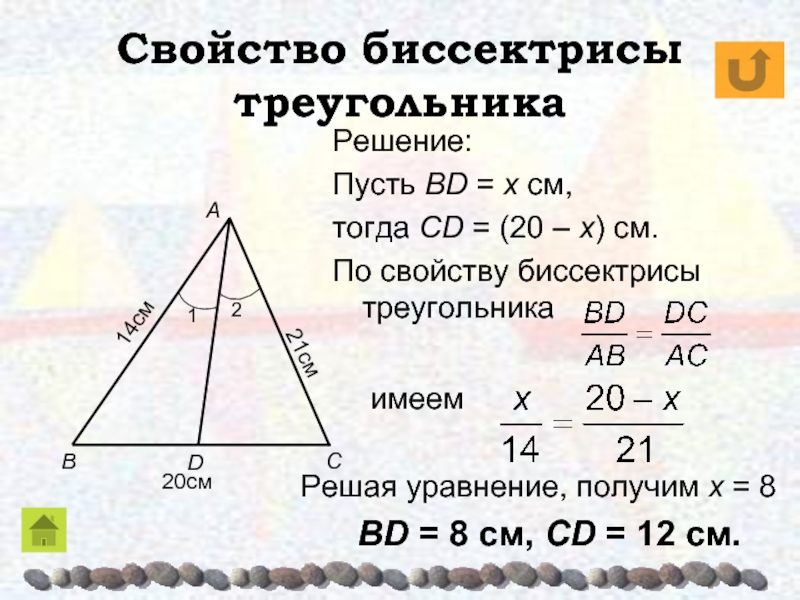
Слайд 21Свойство биссектрисы треугольника
Решение:
Пусть BD = x см,
тогда CD =
(20 – x) см.
По свойству биссектрисы треугольника
имеем
Решая уравнение, получим
х = 8BD = 8 см, CD = 12 см.
Слайд 22Признаки подобия треугольников
Первый признак подобия треугольников.
(по двум углам)
Второй признак подобия
треугольников.
(по углу и двум пропорциональным сторонам)
Третий признак подобия треугольников.
(по трем
пропорциональным сторонам)
Слайд 23Первый признак подобия треугольников.
Если два угла одного треугольника соответственно равны
двум углам другого треугольника, то такие треугольники подобны.
Слайд 24Первый признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1, ∠A =∠A1,
∠B = ∠B.
Доказать:
ΔABC
~ ΔA1B1C1
Доказательство:
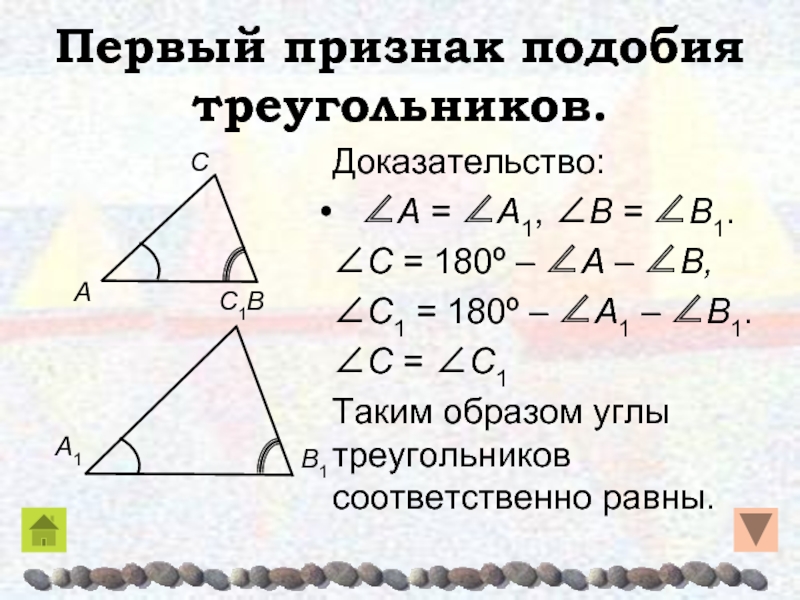
Слайд 25Первый признак подобия треугольников.
Доказательство:
∠A = ∠A1, ∠B
= ∠B1.
∠C = 180º – ∠A – ∠B,
∠C1 = 180º
– ∠A1 – ∠B1.∠C = ∠C1
Таким образом углы треугольников соответственно равны.
Слайд 26Первый признак подобия треугольников.
Доказательство:
∠A = ∠A1,
∠B = ∠B1.
Имеем
Аналогично, рассматривая равенство углов ∠C=∠C1, ∠A=∠A1,
получимИтак, сходственные стороны пропорциональны.
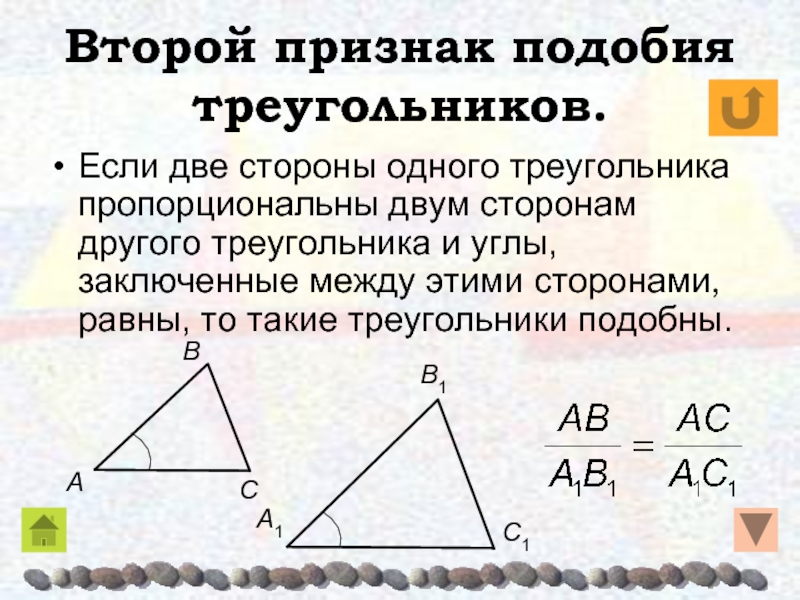
Слайд 27Второй признак подобия треугольников.
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, заключенные между этими сторонами,
равны, то такие треугольники подобны.
Слайд 28Второй признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1,
∠A =∠A1,
Доказать:
ΔABC ~
ΔA1B1C1
Доказательство:
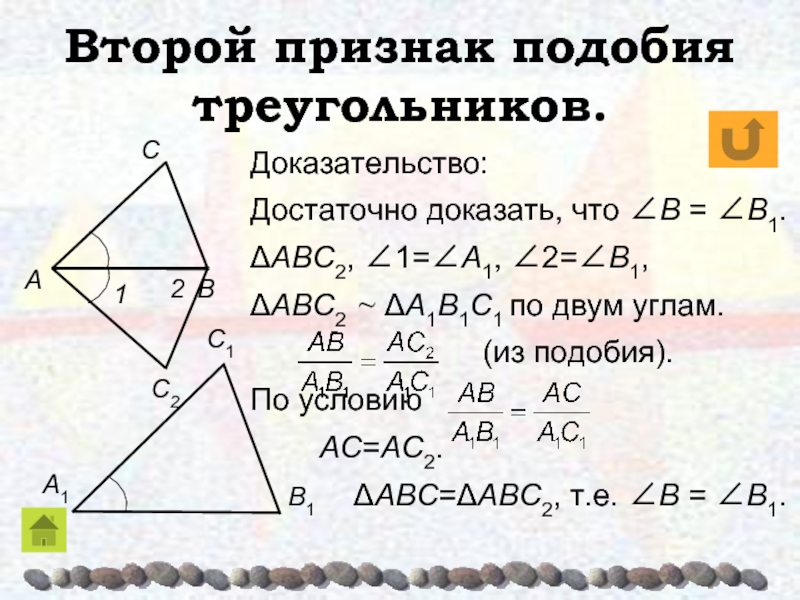
Слайд 29Доказательство:
Достаточно доказать, что ∠B = ∠B1.
ΔABC2, ∠1=∠A1, ∠2=∠B1,
ΔABC2 ~ ΔA1B1C1
по двум углам.
(из подобия).По условию
AC=AC2.
ΔABC=ΔABC2, т.е. ∠B = ∠B1.
Второй признак подобия треугольников.
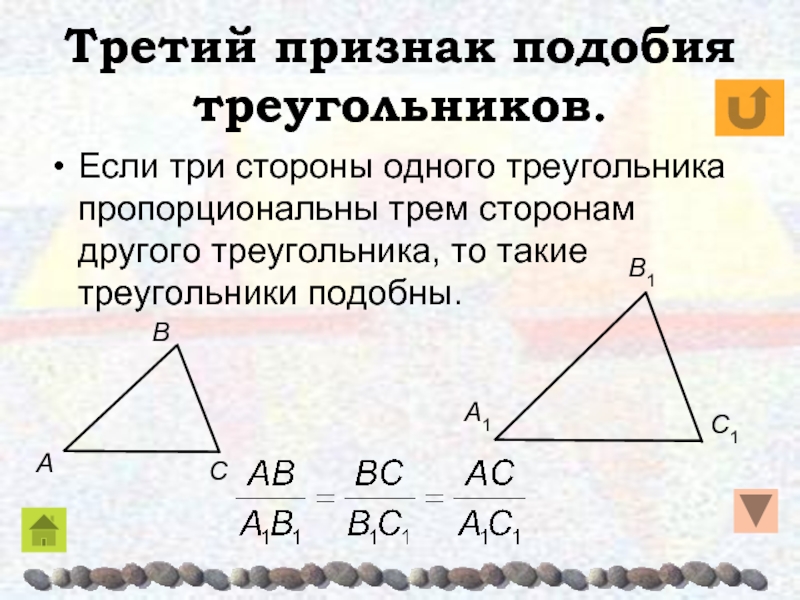
Слайд 30Третий признак подобия треугольников.
Если три стороны одного треугольника пропорциональны
трем сторонам другого треугольника, то такие треугольники подобны.
Слайд 31Третий признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1,
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Слайд 32Третий признак подобия треугольников.
Доказательство:
Достаточно доказать, что ∠A=∠A1
ΔABC2, ∠1=∠A1, ∠2=∠B1,
ΔABC2
~ ΔA1B1C1 по двум углам.
Отсюда
По условию
ΔABC=ΔABC2 по трем сторонам, т.е. ∠A = ∠A1
Слайд 33Разминка
1
Отрезки AB и CD пропорциональны отрезкам MN и PK.
Найдите MN,
если AB = 3, CD = 4, PK = 2.
MN
= 1,5
Слайд 34Разминка
2
Даны два подобных прямоугольных треугольника.
Коэффициент подобия 1,5
Стороны одного из
них 3, 4 и 5.
Найдите гипотенузу другого.
7,5
5 · 1,5
= 7,5
Слайд 37Разминка
5
Отношение площадей двух квадратов равно 9 : 1.
Найдите сторону
большего их них, если сторона меньшего равна 2.
6
k2 = 9,
k = 3 Коэффициент подобия
3 · 2 = 6
сторона большего квадрата
Слайд 391 задача
Отрезки AB и CD пропорциональны отрезкам EF и MN.
Найдите EF,
если AB = 5 см, CD = 80
мм, MN = 1 дм.Слайд 417 задача
Треугольник со сторонами 2 см, 3 см, 4 см
подобен
треугольнику
со сторонами 5 мм, 7,5 мм и 1 см.
Найдите коэффициент подобия.
Слайд 4210 задача
Сходственные стороны подобных треугольников относятся как 1 : 3.
Найдите периметр большего треугольника, если периметр меньшего 15 см.
Слайд 4313 задача
ΔABC ~ ΔA1B1C1 ,
AB : A1B1 = k
= 4
SΔABC= 48 м2.
Найдите площадь треугольника A1B1C1 .
Слайд 442 задача
В параллелограмме ABCD диагонали пересекаются в точке О, CD
= 10 см.
Найдите периметр параллелограмма, если
Слайд 455 задача
Основание равнобедренного треугольника равно 18 мм,
а биссектриса делит боковую
сторону на отрезки, из которых прилежащий к основанию равен 12
мм. Найдите периметр треугольникаСлайд 468 задача
Треугольники KPF и ЕМТ подобны, причем
∠F = 20°,
∠E = 40°.
Найдите остальные углы этих треугольников.
Слайд 4711 задача
Периметры подобных треугольников
12 мм и 108 мм соответственно.
Стороны
одного из них 3 мм, 4 мм и 5 мм.
Найдите
стороны другого и определите его вид.
Слайд 4814 задача
Площади двух подобных треугольников равны 16 см2 и 25
см2.
Одна из сторон первого треугольника равна 2 см.
Найдите
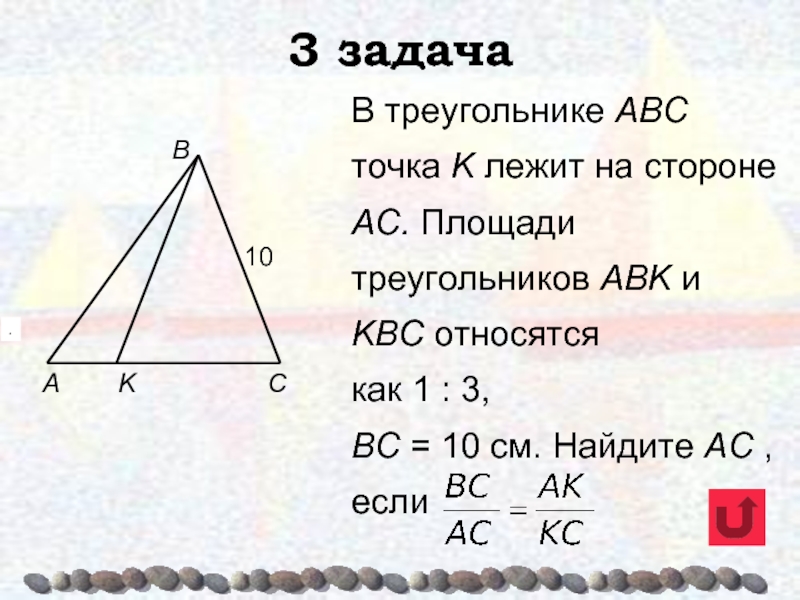
сходственную ей сторону второго треугольника. Слайд 49В треугольнике ABC точка K лежит на стороне АС. Площади
треугольников АВK и KВС относятся
как 1 : 3,
ВС
= 10 см. Найдите AC , если 3 задача
.
.
Слайд 5212 задача
Масштаб плана 1 : 1000.
Какова длина ограды участка,
если
на плане размеры
прямоугольника,
изображающего участок 2 см х 5
см.Слайд 5315 задача
Периметры подобных треугольников относятся как 2 : 3,
сумма
их площадей равна 260 см2. Найдите площадь каждого треугольника.
Слайд 54ЗАДАЧИ
1.
Диагонали трапеции ABCD пересекаются в точке O. Площади треугольников BOC
и AOD относятся как 1 : 9. Сумма оснований BC
и AD равна 4,8 см. Найдите основания трапеции.Решение:
Слайд 55Решение
Рассмотрим ΔAOD и ΔBOC:
∠1=∠2 (накрест лежащие при
AD || BC, и секущей AC;
∠3=∠4 (вертикальные)
ΔAOD
~ ΔBOC (по двум углам)= k
A
B
C
D
O
1
2
4
3
Слайд 56Решение
.
k = 3
AD + BC =
= 3BC + BC = 4BC
AD + BC = 4,8см
(по условию)
BC = 1,2 см
AD = 3,6 см
Ответ: BC = 1,2 см AD = 3,6 см
Слайд 57ЗАДАЧИ
2.
Докажите, что треугольники, изображенные на рисунке, подобны, и выясните взаимное
положение прямых CB и DF.
Решение:
Слайд 58Решение
Отсюда
ΔABC~ΔDEF
по трем пропорциональным сторонам
Найдем отношение сходственных сторон данных
треугольников
Слайд 59Решение
ΔABC~ΔDEF
Соответственно
∠A = ∠E
∠B = ∠F
∠ACB = ∠EDF
E
.
Рассмотрим
прямые BC и DF, секущую AE
∠1 = ∠2
(внешние накрест лежащие)
BC || DF.
Слайд 60ЗАДАЧИ
3.
Отрезки AB и CD пересекаются
в точке O, причем
.
Докажите,
что ∠CBO = ∠DAO. Решение:
Слайд 61Решение
Рассмотрим ΔAOD и ΔCOB
∠DOA = ∠COB (вертикальные).
.
ΔAOD ~ ΔCOB по углу и двум пропорциональным сторонам.
∠CBO = ∠DAO (из подобия).
A
O
C
B
D
Слайд 62ЗАДАЧИ
4. В треугольнике ABC
AB =
4, BC = 6, AC = 7.
Точка E лежит
на стороне AB. Внутри треугольника взята точка M так,
что MB = 5,25, ME = 4,5, AE = 1.
Прямая BM пересекает AC в точке P.
Докажите, что ΔAPB равнобедренный.
Решение:
Слайд 63Решение
.
Рассмотрим ΔBEM и ΔABC
BE = AB − AE = 4 – 1 = 3
BE : AB = 3 : 4 = 0,75
EM : BC = 4,5 : 6 = 0,75
BM : AC = 5,25 : 7 = 0,75,
т.е. стороны треугольников
пропорциональны
B
E
P
C
A
M
7
6
4
4,5
5,25
1
Слайд 64
ΔBEM ~ ΔABC по трем пропорциональным сторонам.
Следовательно, ∠BME =
∠AСB
∠EBM = ∠BAC ∠BEM = ∠ABC.
Рассмотрим треугольник ABP:
∠EBM = ∠BAC, т.е. ∠ABP = ∠BAP.
ΔABP – равнобедренный, что и требовалось доказать.
Решение
Слайд 65ЗАДАЧИ
5.
Диагональ AC параллелограмма ABCD равна 90.
Середина M стороны AB
соединена с вершиной D.
Отрезок MD пересекает AC в точке
O. Найдите отрезки AО и CО.
Решение:
Слайд 66Рассмотрим
ΔAOM и ΔCОD
∠AOM = ∠CОD (вертикальные),
∠MAO =
∠ ОCD (накрест лежащие при AB || DC и секущей
AC).Отсюда ΔAOM ~ ΔCОD
по двум углам.
Решение
C
Слайд 67
Решение
C
ΔAOM ~ ΔCОD
.
AM = ½
AB (по условию)
AB = CD (ABCD - параллелограмм),
AM
: CD = 1 : 2т.е. AO = 0,5CО
AO = ⅓AC = ⅓·90 = 30
CO = ⅔AC = ⅔·90 = 60
Слайд 72ТЕСТ
4) По данным рисунка площади данных треугольников относятся
А) 3
: 1
Б) 9 : 1
В) 6 : 1
Г) 9 :
4
Слайд 75Помощь в управлении
презентацией
управление презентацией осуществляется с помощью левой клавиши
мыши
переход от одного слайда к другому и на гиперссылки по
одиночному щелчкузавершение презентации при нажатии кнопки выход
Возврат в содержание
Переход по слайдам
Возврат к гиперссылке
Справка