Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие многогранника
Содержание
- 1. Понятие многогранника
- 2. Вступление Понятие многогранника Характеристика Эйлера Призма Решение задач Домашнее заданиеСодержание.
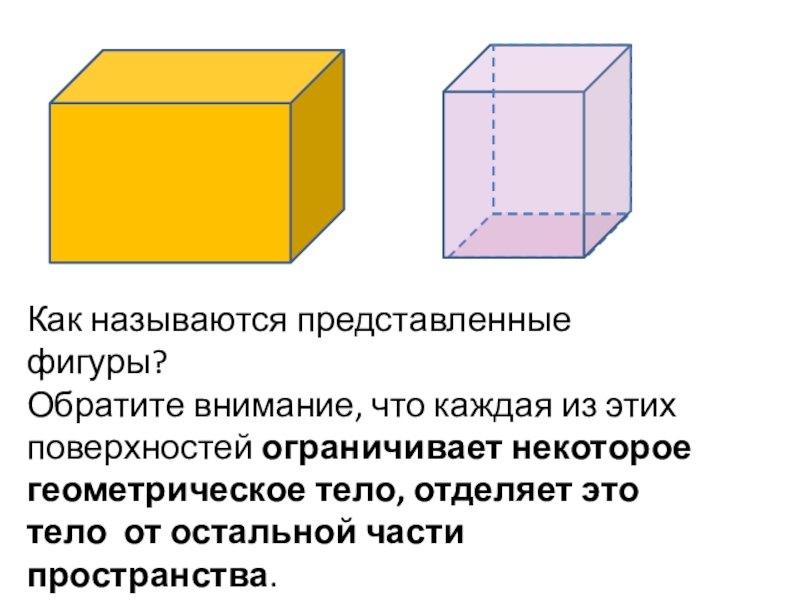
- 3. Как называются представленные фигуры?Обратите внимание, что каждая
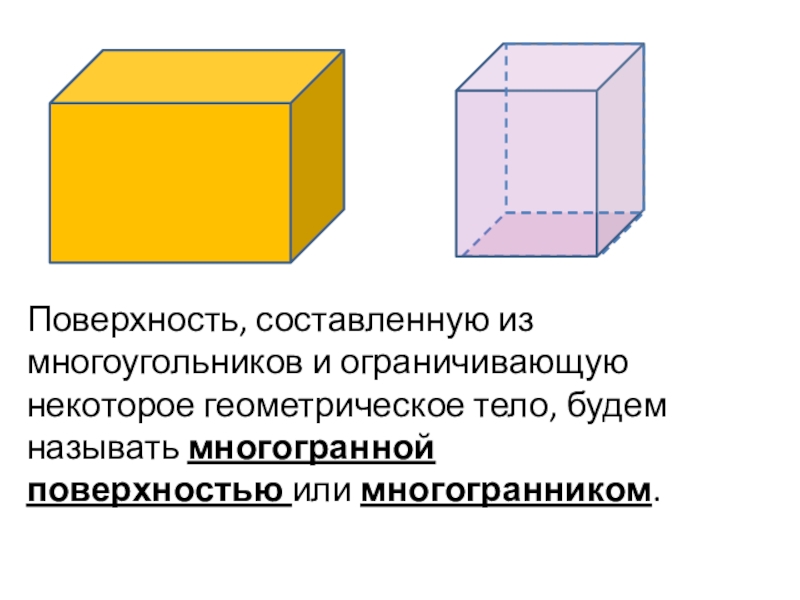
- 4. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
- 5. Многие строения в окружающем нас мире имеют форму многогранников или состоят из нескольких разных многогранников
- 6. Поэтому для лучшей сохранности, эксплуатации и моделирования
- 7. Многие многогранники изобрёл не человек, а создала природа в виде кристаллов:Поваренная и каменная сольГорный хрустальКристаллы льда
- 8. Кристаллы кварцаКристаллы граната
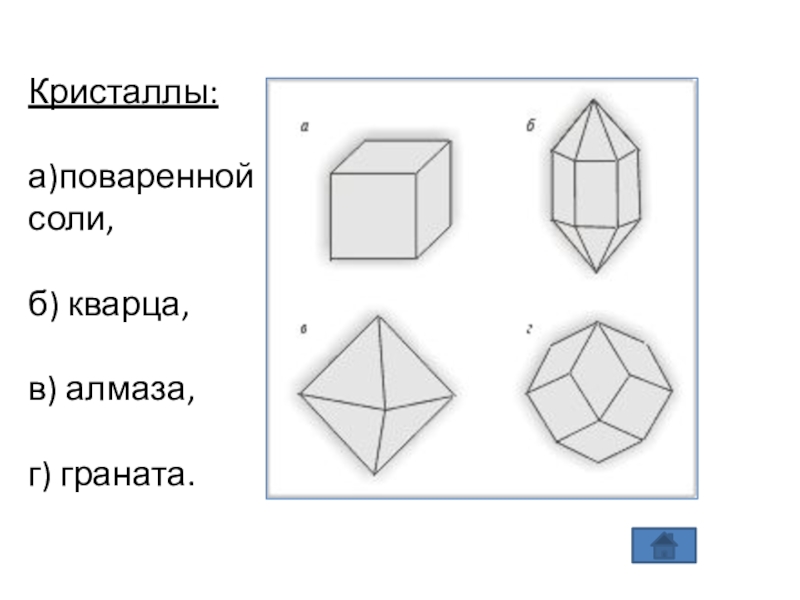
- 9. Кристаллы:а)поваренной соли,б) кварца,в) алмаза,г) граната.
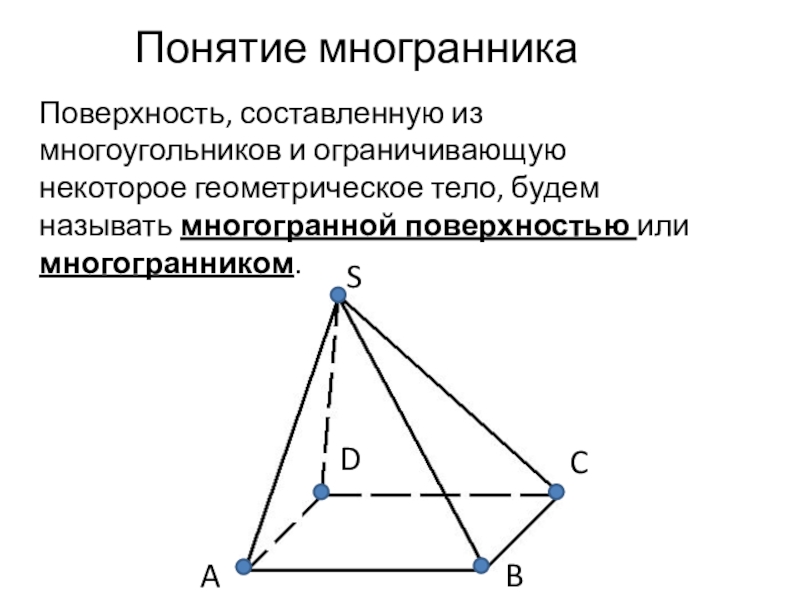
- 10. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.Понятие многранника
- 11. Из чего состоит поверхность многогранника?Из многоугольников .Значит
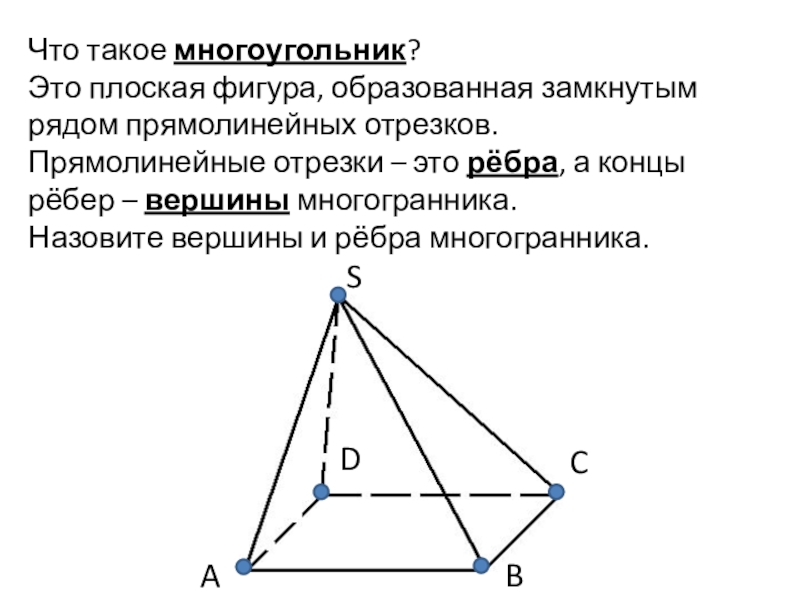
- 12. Что такое многоугольник?Это плоская фигура, образованная замкнутым
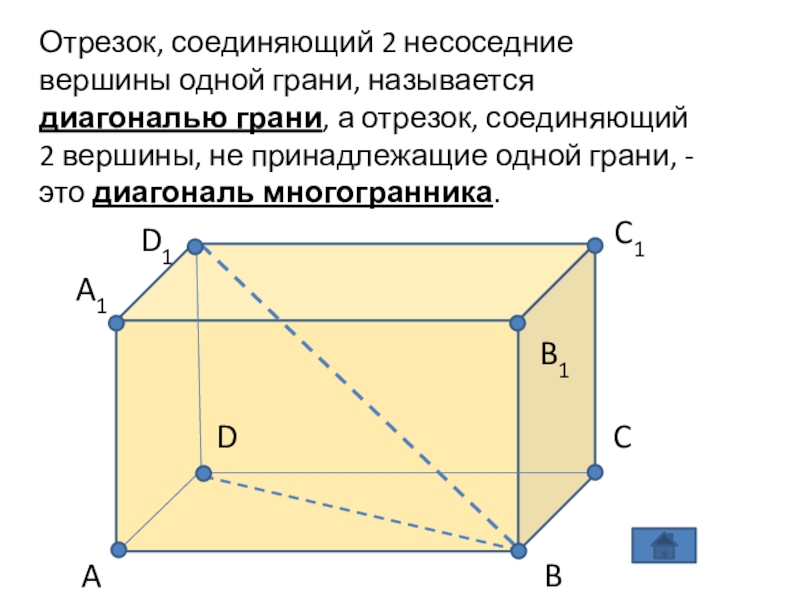
- 13. Отрезок, соединяющий 2 несоседние вершины одной грани,
- 14. Характеристика ЭйлераРавенство, которое выражает Эйлерову характеристику, было
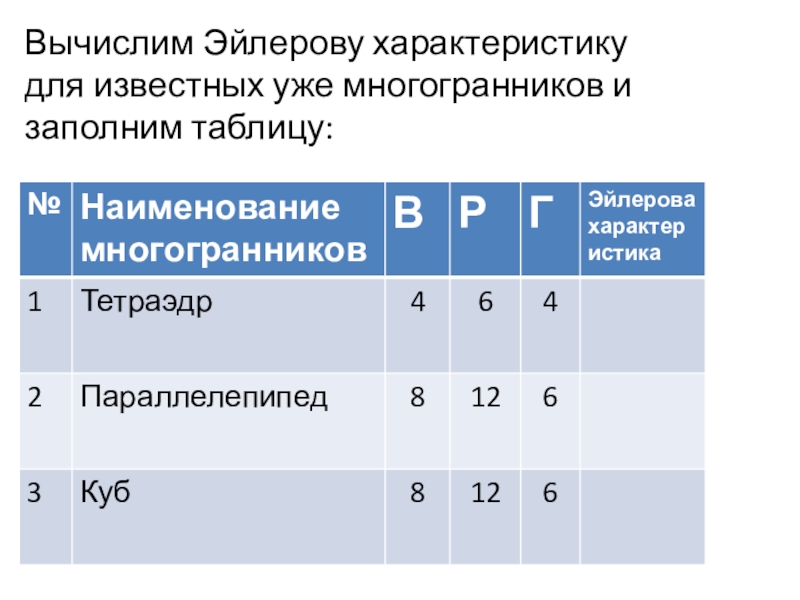
- 15. Вычислим Эйлерову характеристику для известных уже многогранников и заполним таблицу:
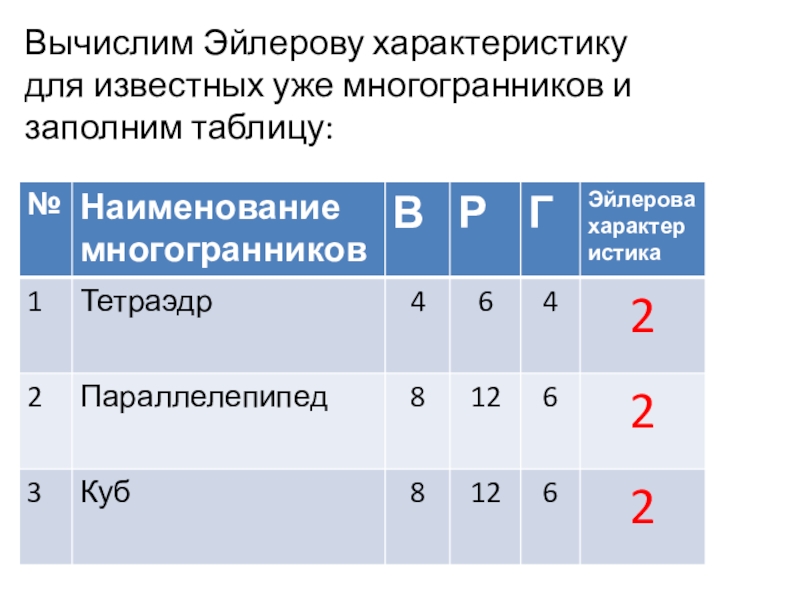
- 16. Вычислим Эйлерову характеристику для известных уже многогранников и заполним таблицу:
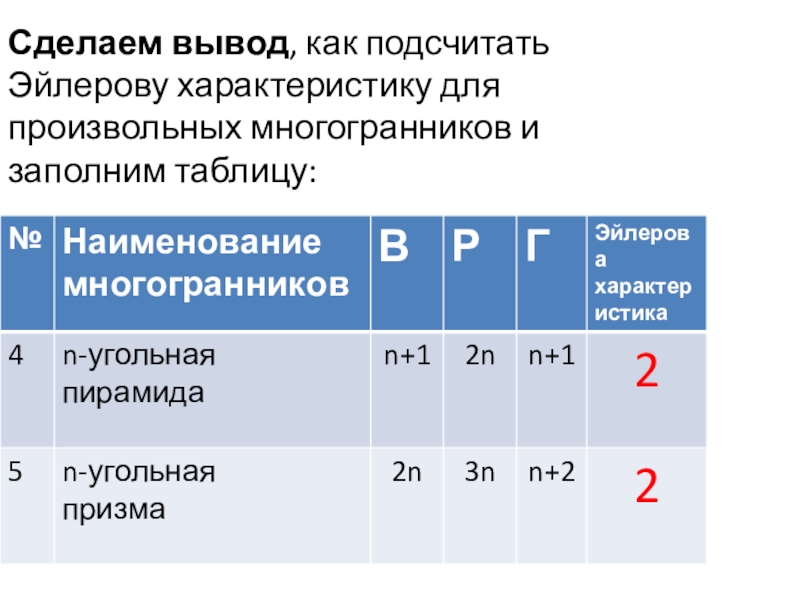
- 17. Сделаем вывод, как подсчитать Эйлерову характеристику для произвольных многогранников и заполним таблицу:
- 18. Многогранник называется выпуклым, если он расположен по
- 19. Призма.Задание классу:К следующему уроку подготовить презентацию «Призма» (пункт 27).
- 20. Решение задач.Задание классу: № 219, 223
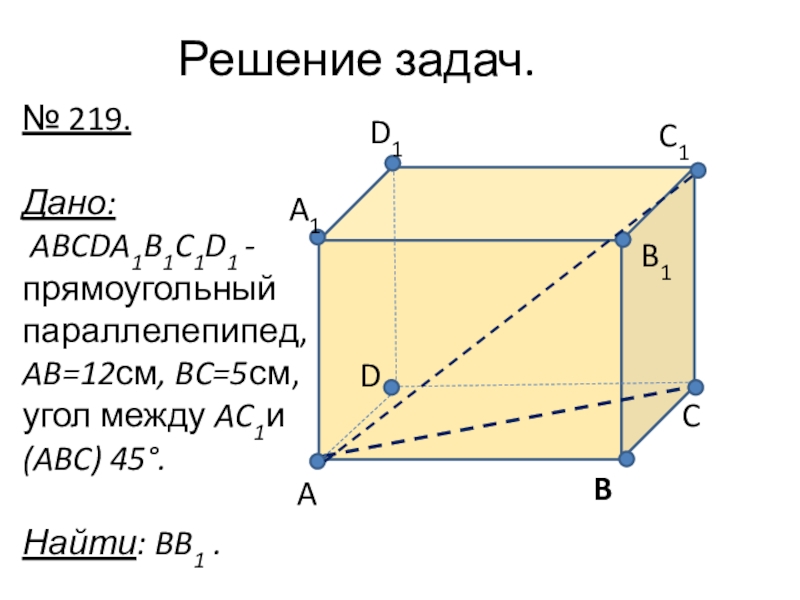
- 21. Решение задач.№ 219.Дано: ABCDA1B1C1D1 -прямоугольный параллелепипед, AB=12см, BC=5см, угол между AC1и (ABC) 45°.Найти: BB1 .ABCB1C1D1A1D
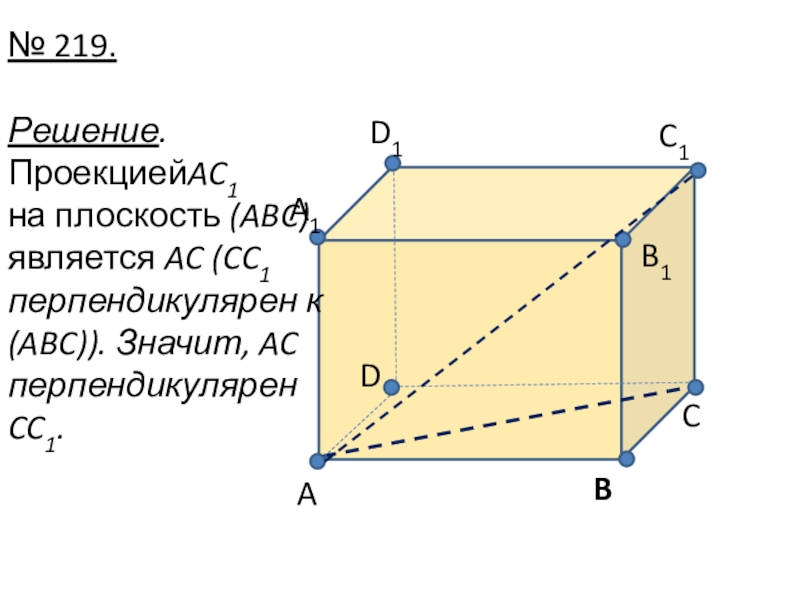
- 22. № 219.Решение.ПроекциейAC1 на плоскость (ABC)является AC (CC1 перпендикулярен к(ABC)). Значит, AC перпендикулярен CC1.ABCB1C1D1A1D
- 23. № 219.Решение.Значит, угол CAC1=45°. Имеем: ΔACC1 прямоугольный
- 24. Домашнее задание.Задание классу:Пункты 25-27, № 220.
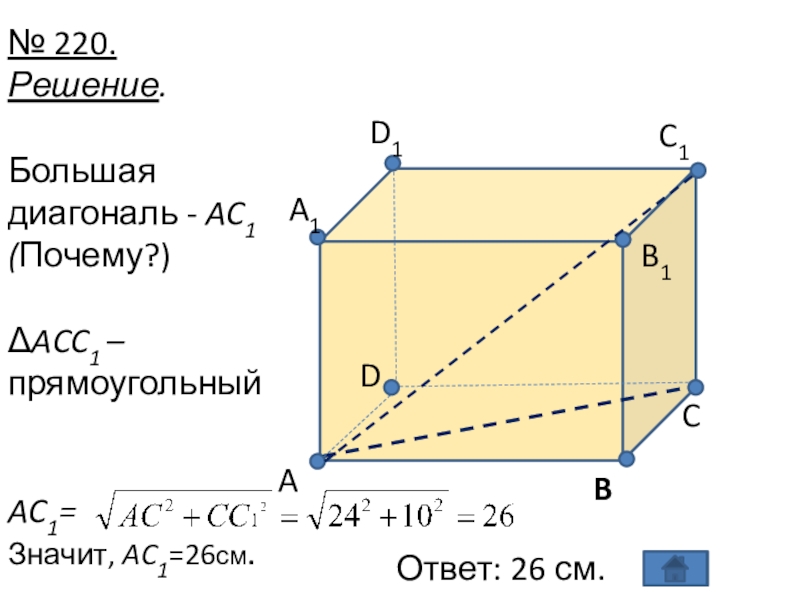
- 25. № 220.Решение.Большая диагональ - AC1 (Почему?)ΔACC1 – прямоугольныйAC1=Значит, AC1=26см. ABCB1C1D1A1DОтвет: 26 см.
- 26. Скачать презентанцию
Вступление Понятие многогранника Характеристика Эйлера Призма Решение задач Домашнее заданиеСодержание.
Слайды и текст этой презентации
Слайд 1Понятие многогранника
Урок геометрии в 10 классе
Работа учителя
математики МОУ «СОШ
№ 94» г. Саратова Яковлевой О.Е.
Слайд 2 Вступление
Понятие многогранника
Характеристика Эйлера
Призма
Решение задач
Домашнее
задание
Содержание.
Слайд 3Как называются представленные фигуры?
Обратите внимание, что каждая из этих поверхностей
ограничивает некоторое геометрическое тело, отделяет это тело от остальной части
пространства.
Слайд 4Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем
называть многогранной поверхностью или многогранником.
Слайд 5Многие строения в окружающем нас мире имеют форму многогранников или
состоят из нескольких разных многогранников
Слайд 6Поэтому для лучшей сохранности, эксплуатации и моделирования здания нужно изучить
свойства многогранников.
Пирамида Хеопса
Памятник относится к эпохе Древнего царства (IV династия).
Построена племянником фараона Хеопса Хемиуном. 
Слайд 7Многие многогранники изобрёл не человек, а создала природа в виде
кристаллов:
Поваренная и каменная соль
Горный хрусталь
Кристаллы льда
Слайд 10Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем
называть многогранной поверхностью или многогранником.
Понятие многранника
Слайд 11Из чего состоит поверхность многогранника?
Из многоугольников .
Значит грани многогранника –
многоугольники.
В данном случае: Δ ASD, ΔASB, ΔDSC, ΔBSC,
четырехугольник ABCD
Слайд 12Что такое многоугольник?
Это плоская фигура, образованная замкнутым рядом прямолинейных отрезков.
Прямолинейные
отрезки – это рёбра, а концы рёбер – вершины многогранника.
Назовите
вершины и рёбра многогранника.
Слайд 13Отрезок, соединяющий 2 несоседние вершины одной грани, называется диагональю грани,
а отрезок, соединяющий 2 вершины, не принадлежащие одной грани, -
это диагональ многогранника.A
D
B
C
B1
C1
A1
D1
Слайд 14Характеристика Эйлера
Равенство, которое выражает Эйлерову характеристику, было им доказано в
1752 году.
Если характеристика Эйлера равна 2, то это выпуклый многогранник.
Вычисляется
характеристика Эйлера следующим образом:В – Р + Г, где В – число вершин, Р – число рёбер, Г – число граней.
Слайд 17Сделаем вывод, как подсчитать Эйлерову характеристику для произвольных многогранников и
заполним таблицу:
Слайд 18Многогранник называется выпуклым, если он расположен по одну сторону от
плоскости каждой его грани.
В противном случае – это невыпуклый многогранник.
Теорема.
В
любом многограннике сумма всех плоских углов при каждой вершине меньше 360°.
Слайд 21Решение задач.
№ 219.
Дано:
ABCDA1B1C1D1 -прямоугольный параллелепипед, AB=12см, BC=5см, угол между
AC1и (ABC) 45°.
Найти: BB1 .
A
B
C
B1
C1
D1
A1
D
Слайд 22№ 219.
Решение.
ПроекциейAC1
на плоскость (ABC)является AC (CC1 перпендикулярен к(ABC)). Значит,
AC перпендикулярен CC1.
A
B
C
B1
C1
D1
A1
D
Слайд 23№ 219.
Решение.
Значит, угол CAC1=45°.
Имеем: ΔACC1 прямоугольный и равнобедренный
AC=CC1=BB1.
Найдём
AC в ΔABC:
AC=
=
Значит,CC1=DD1=13см.
A
B
C
B1
C1
D1
A1
D
Ответ: 13 см.
Слайд 25№ 220.
Решение.
Большая диагональ - AC1 (Почему?)
ΔACC1 – прямоугольный
AC1=
Значит, AC1=26см.
A
B
C
B1
C1
D1
A1
D
Ответ:
26 см.
