Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока "Правила сложения и умножения в комбинаторики"
Содержание
- 1. Тема урока "Правила сложения и умножения в комбинаторики"
- 2. Тип урока: усвоение и закрепление новых знанийЦели
- 3. Организационный этап
- 4. Отгадай ребус ГЛ = К
- 5. Актуализация знаний Что такое комбинаторика? Комбинаторика –
- 6. Слайд 6
- 7. В Древней Грецииподсчитывали число различных комбинаций длинных
- 8. Готфрид Вильгельм
- 9. Для вывода формул автор использовал наиболее простые
- 10. Практическая деятельность по изучению
- 11. Правило суммыЕсли пересечение конечных множеств А и
- 12. Задача №1.На одной полке книжного шкафа стоит
- 13. Правило умножения.Если множества А и В конечны,
- 14. Задача № 2Пусть существует три кандидата на
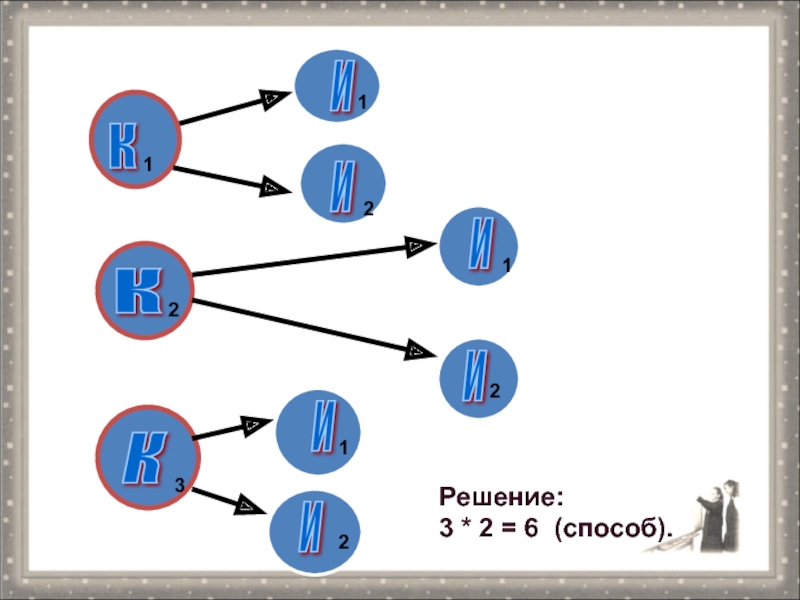
- 15. кккииииии111123222Решение:3 * 2 = 6 (способ).
- 16. 1.Имеется 3 вида конвертов и 4 вида
- 17. Проверка и закрепление освоенногоГрупповая форма.Упражнения на закрепление
- 18. 1. Сколькими способами можно записать в виде
- 19. Самостоятельная работа 1 вариант.1. Сколько можно составить
- 20. Рефлексия, подведение итоговАнкета:На уроке я работал
- 21. Домашнее задание Придумайте, какую комбинаторную задачу может решать: повар, диспетчер автовокзала, домохозяйка, завуч школы
- 22. Спасибо за урок!
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Тип урока: усвоение и закрепление новых знаний
Цели урока:
Предметные:отработка правил
сложения и вычитания вероятностей; умение выделять главное и существенное при
установлении типа комбинаторных задач.Метапредметные: умение контролировать процесс и результат учебной и математической деятельности.
Личностные: проявлять интерес к изучению темы и желание применить приобретенные знания и умения.
Слайд 3Организационный этап
.
.
Эпиграф урока:
«Число,
место и комбинация – три взаимно перекрещивающиеся, но отличные сферы
мышления, к которым можно отнести все математические идеи».Дж. Сильвестр
Слайд 5Актуализация знаний
Что такое комбинаторика?
Комбинаторика – это раздел математики,
посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям.
Здесь
изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Латинское слово combinare означает «соединять, сочетать».
Слайд 6 Из истории комбинаторики
С
комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае
увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
Слайд 7В Древней Греции
подсчитывали число различных комбинаций длинных и коротких слогов
в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые
можно составить из частей и т.д.Со временем появились различные игры
(нарды, карты, шашки, шахматы и т. д.)
В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.
Слайд 8 Готфрид Вильгельм Лейбниц
(1.07.1646 - 14.11.1716)
Комбинаторику, как самостоятельный раздел математики первым
стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».Леонард Эйлер(1707-1783)
рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.
Слайд 9Для вывода формул автор использовал наиболее простые и наглядные методы,
сопровождая их многочисленными таблицами и примерами. Сочинение Я. Бернулли превзошло
работы его предшественников и современников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью не только как серьёзного научного трактата, но и как учебно-справочного издания.Слайд 10 Практическая деятельность по изучению
нового материала
Методы решения комбинаторных
задачПравило суммы.
2. Правило произведения
Слайд 11Правило суммы
Если пересечение конечных множеств А и В пусто, то
число элементов в их объединении равно сумме чисел элементов множеств
А и В :Слайд 12Задача №1.
На одной полке книжного шкафа стоит 30 различных книг,
а на другой – 40 различных книг (не такие как
на первой). Сколькими способами можно выбрать одну книгу.Решение:
30 + 40 = 70 (способами).
Слайд 13Правило умножения.
Если множества А и В конечны, то число N
возможных пар (а; в), где а из А, в из
В равно произведению чисел элементов этих множеств:N = n (A) *n (B)
Слайд 14Задача № 2
Пусть существует три кандидата на пост командира и
2 на пост инженера. Сколькими способами можно сформировать экипаж корабля,
состоящий из командира и инженера?Слайд 161.Имеется 3 вида конвертов и 4 вида марок. Сколько существует
вариантов
выбора конверта с маркой?
2.В кружке 6 учеников. Сколькими способами
можно выбрать старостукружка и его заместителя?
4. В буфете есть 4 сорта пирожков. Сколькими способами ученик может
купить себе 2 пирожка?
3.Концерт состоит из 5 номеров. Сколько имеется вариантов программы
этого концерта?
Слайд 17Проверка и закрепление освоенного
Групповая форма.
Упражнения на закрепление навыков решения задач
(группы решают задачи разными способами и предлагают свои решения классу,
обсуждаются достоинства и недостатки), решения оформляются в тетрадях и на доске.Слайд 181. Сколькими способами можно записать в виде произведения простых множителей
число 30?
2. Сколько диагоналей в выпуклом десятиугольнике?
3. Встретились несколько друзей
и все обменялись рукопожатиями. Всего было сделано 15 рукопожатий. Сколько встретилось друзей?4. Сколько словарей надо создать, чтобы можно было непосредственно выполнять перевод с любого из пяти языков на любой другой из этих языков?
5. Из 100 человек 85 знают английский, 80 - испанский, 75 - немецкий. Сколько человек заведомо знают все три языка?
6. Придумайте как можно больше комбинаторных задач с использованием данных объектов: Четверо друзей: Катя, Олег, Света, Андрей.
Слайд 19Самостоятельная работа
1 вариант.
1. Сколько можно составить четырехзначных чисел из
цифр 1, 5, 8, 3, если: а) цифры в числе
не повторяются;б) цифры могут повторяться.
2. В среду в 5 «Б» классе 5 уроков: русский, информатика, естествознание, ИЗО, иностранный. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что информатика –первый урок?
1. Сколько можно составить трехзначных чисел из цифр 4, 9, 7, если: а) цифры в числе не повторяются;
б) цифры могут повторяться.
2. В среду в 5 «А» классе 5 уроков: русский, литература, естествознание, математика, иностранный. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что математика – второй урок?
Слайд 20Рефлексия, подведение итогов
Анкета:
На уроке я работал - активно/ пассивно
Своей
работой на уроке я - доволен/ не доволен
Урок для
меня показался - коротким/ длинным, полезным/ бесполезным, интересен/ скученНа уроке я - устал/ не устал
Мое настроение стало - лучше/ стало хуже
Материал урока был мне - понятен/ не понятен