Понятие площади фигуры и её измерение

называют равными.
Какие фигуры называют равновеликими.
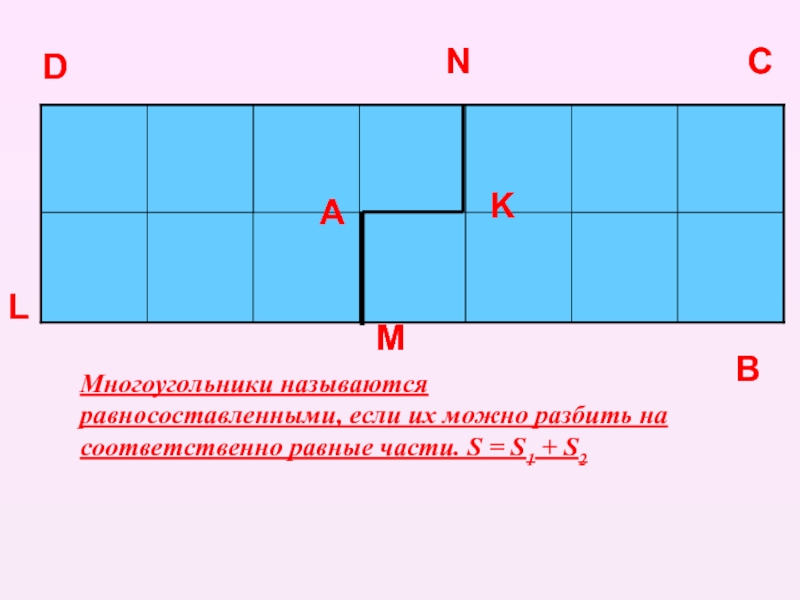
Какие фигуры называют равносоставленными.
Единицы измерения площади.

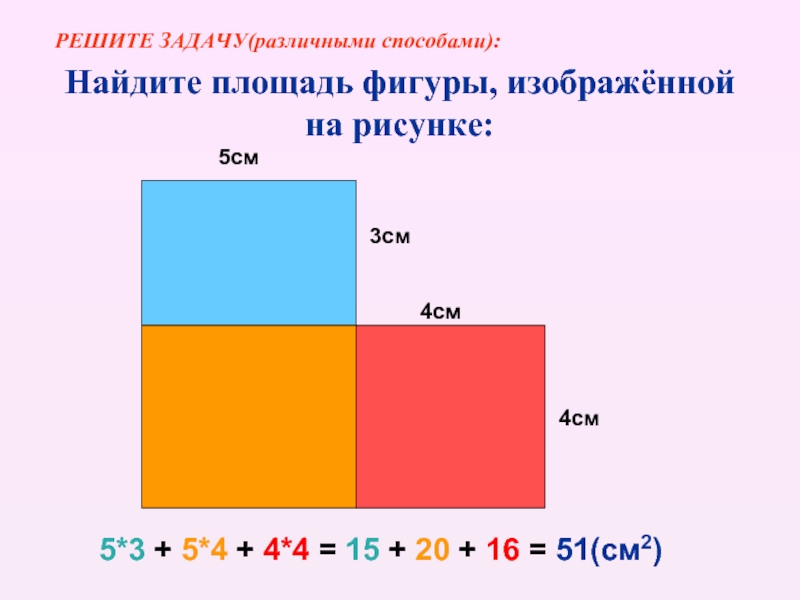
Формулу площади прямоугольника, квадрата.
Какая величина называется скалярной.
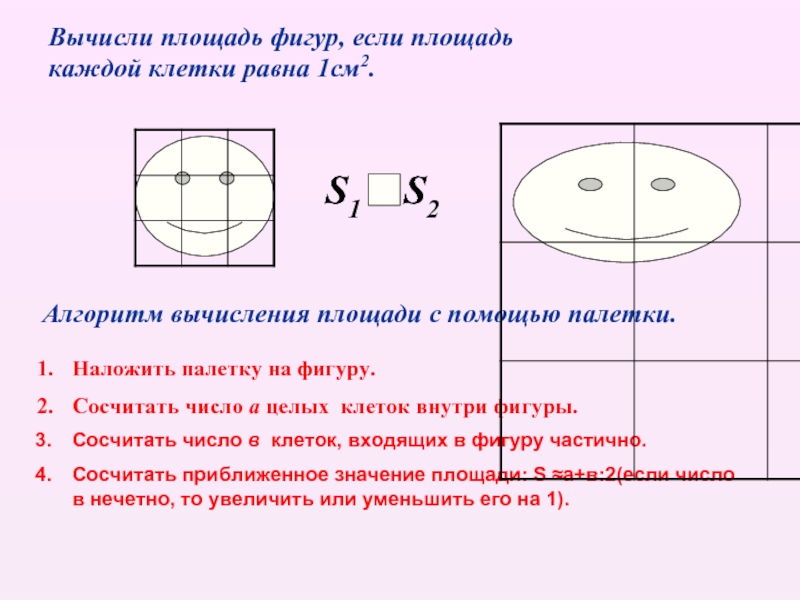
Что такое палетка?

Узнаете:

Вспомните:

га.
1 га =10 000 м2 1 м2=10 000

см2 1 м2=100 дм2 1 км2=1 000 000 м2

Площадь прямоугольника
равна произведению длин соседних его сторон.
5 . 3=15 ( квадратов)

S = a b
При a=5, b=3 получим:
S= 5 . 3=15(см2)

Площадь квадрата равна квадрату длины его стороны.
S = a2

15 см2

а

в

объем, масса, время, стоимость и количество)



а
b
1см
Инструмент, с помощью которого находят

приближенное значение площади, называется палеткой.

15 см2

S = ab
При a=5, b=3 получим:
S= 5 . 3=15(см2)

фигуры так, что:
Равные фигуры имеют равные площади;
Если фигура состоит из

двух частей, то ее площадь равна сумме площадей этих частей

7 см2

значения их площадей, т. е. F1 = F2 ⇒ S(F1)=S(F2)
2.

Если фигура F состоит из фигур F1 и F2 , то численное значение площади фигуры равно сумме численных значений площадей фигур F1 и F2 ,т.е. S(F1⊕F2)=S(F1)+S(F2)
3. Численное значение площади единичного квадрата принимается равным 1, т.е. S(E) =1.
4. При замене единицы площади численное значение площади фигуры F увеличивается ( уменьшается) во столько раз, во сколько новая единица меньше (дольше) старой.
5. Если фигура F1 является частью фигуры F2 ,то численное значение площади фигуры F1 не больше численного значения площади фигуры F2 , т.е. F1 ⊂ F2 ⇒ S(F1)≤S(F2)

5см.
Дано:

a = 10дм,
b = 5см.
Найти S.
Решение.
S =

a b.

10дм=100см.
S = 100 * 5 =500(см2).

ЗАДАЧА №1.

раза меньше. Чему равна площадь коридора?
Дано:
a = 28м,
b –

в 4 раза меньше

Найти S.

Решение.

S = a b, b - ?

b = 28 : 4 = 7(м).

S = 28 * 7 = 196(м2).

Ответ: 196м2.

ЗАДАЧА №2

= 15 + 20 + 16 = 51(см2)
РЕШИТЕ ЗАДАЧУ(различными способами):

Sn=6а2
S = 6*42 =96(cм2)

ЗАДАЧА №4
Найдите площадь полной поверхности куба.
Ответ:

96 см2

наложить на вторую, что эти фигуры совпадут.

части. S = S1 + S2

ли, что равносоставленные фигуры всегда равновелики?
Верно ли, что равновеликие фигуры

всегда равносоставленные?
Верно ли, что любые два равновеликих многоугольника всегда равносоставлены?

(Дом. задание. Л.П.Стойлова, стр.442-448.)

площади с помощью палетки.
Наложить палетку на фигуру.
Сосчитать число а целых

клеток внутри фигуры.
Сосчитать число в клеток, входящих в фигуру частично.
Сосчитать приближенное значение площади: S ≈а+в:2(если число в нечетно, то увеличить или уменьшить его на 1).

S1 = S2