Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока "Неравенства"
Содержание
- 1. Презентация для урока "Неравенства"
- 2. Числовое неравенствоНера́венство — одно из фундаментальных понятий математики.Если
- 3. Неравенства одинакового и противоположного смыслаНеравенства
- 4. Строгие и нестрогие неравенства НеравенстваСтрогиеНестрогиеНеравенства отношений >,
- 5. Свойства числовых неравенствСвойство 1. Если a >
- 6. Обоснование свойства 1, при помощи числовой прямой
- 7. Свойство 2. Если a > b,
- 8. Свойство 3.Если a > b и m
- 9. Свойство 4.Если a > b и c
- 10. Свойство 5.Если a, b, c, d –
- 11. Свойство 6.Если а и b — неотрицательные
- 12. Пример 1.Пусть a и b - положительные
- 13. Пример 2.Пусть а — положительное число. Доказать, чтоРешение. Получили неотрицательное число, значит, Заметим, что
- 14. Пример 3.Пусть а и b неотрицательные числа.
- 15. В этом случае, число
- 16. Использованные ресурсыУчебник «Алгебра» А.Г. Мордкович 8 классhttp://ru.wikipedia.org/wikiЯндекс картинки
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Числовое неравенство
Нера́венство — одно из фундаментальных понятий математики.
Если два вещественных числа a и
b соединены знаком неравенства ≠ или одним из отношений
порядка a > b , илиa < b или a ≥ b , или же a ≤ b , установленных между числами, то говорят, что задано числовое неравенство.
Если a > b – это значит, что a – b – положительное число;
Если a < b - это значит, что a – b – отрицательное число;
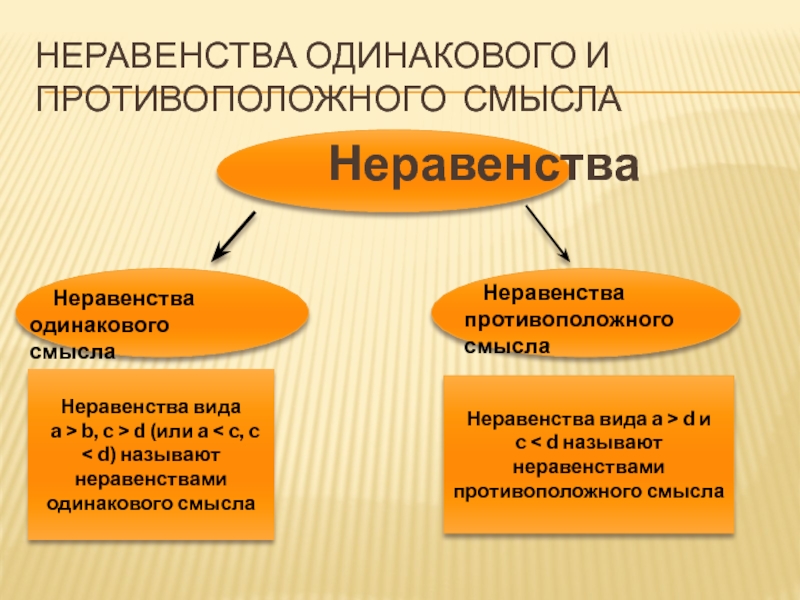
Слайд 3Неравенства одинакового и противоположного смысла
Неравенства
Неравенства
одинакового смысла
Неравенства противоположного смысла
Неравенства
вида a > b, c > d (или a < c, c < d) называют неравенствами одинакового смысла
Неравенства вида a > d и
c < d называют неравенствами противоположного смысла
Слайд 4Строгие и нестрогие неравенства
Неравенства
Строгие
Нестрогие
Неравенства отношений >,
называют нестрогими
Слайд 5Свойства числовых неравенств
Свойство 1.
Если a > b и
b > c, то a > c
Доказательство.
1) a >
b – по условию, т.е. a - b – положительное число. 2) b > c – по условию, т.е. b - c – положительное число.
3) Сложив положительные числа a - b и b - c, получим положительное число.
4) Следовательно, (a - b) + (b - c) = a - c. Значит, a - c – положительное число , т.е a > c, что и требовалось доказать.
Слайд 6Обоснование свойства 1, при помощи числовой прямой
Неравенство a
> b означает, что на числовой прямой точка a расположена
правее точки b, а неравенство b > c - что точка b расположена правее точки c. Но тогда точка a расположена на прямой правее точки c, т.е. a > c. Это свойство называют свойством транзитивности (Образно говоря, от пункта a мы добираемся до пункта c как бы транзитом, с промежуточной остановкой в пункте b)c
b
a
x
Слайд 7Свойство 2.
Если a > b, то a + c
> b + c
То
есть, если к обеим частям неравенства прибавить одно и тоже число, то знак неравенства не изменится.Пример:
6 > 4 , если к обеим частям неравенства прибавить 2 , то знак неравенства не изменится. Получится такое выражение: 8 > 6. На основе первого свойства можно сделать вывод, что любое слагаемое можно перенести из одной части в другую, изменив его знак на противоположный. Пример:
5 < 9, в этом неравенстве можем правую часть перенести в левую, а левую в правую, и знак неравенств не поменяется: -9 < 5
Слайд 8Свойство 3.
Если a > b и m > 0 ,
то a b
m mТо есть, если обе части неравенства разделить на одно и то же положительное число, то знак неравенства следует сохранить;
Пример: a > b , тогда a b
Если а > b и m > 0, то am> bm
То есть, если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить;
Пример: a > b , тогда 8a > 8b
Если а > b и m < 0, то am < bm.
То есть, если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на < ).
Пример: a < b, тогда -9a > -9b;
Если a > b, то -a <-b;
То есть, если изменить знаки у обеих частей неравенства, то надо изменить и знак неравенства.
8
8
Слайд 9Свойство 4.
Если a > b и c > d, то
a + c > b + d.
Доказательство.
I способ.
1. а > b и с > d - по условию, значит, а - b и с - d — положительные числа. 2. Тогда и их сумма, т. е. (а - b) + (с - d) — положительное число.
3. Так как (a-b) + (c-d) = (a + c)-(b + d), то и (а + с) - (b + d) — положительное число. Поэтому a + c > b + d, что и требовалось доказать.
II способ.
1.Так как а > Ь, то а + с > b + с – по свойству 2.
2. Аналогично, так как с > d, то с + b > d + b.
3.Итак, а + с > b + с, b + с > b + d. Тогда, в силу свойства транзитивности, получаем, что а + с > b + d, что и требовалось доказать.
Слайд 10Свойство 5.
Если a, b, c, d – положительные числа и
a > b, c > d, то
ac > bd.То есть, при умножении неравенств одинакового смысла, у которых левые и правые части — положительные числа, получится неравенство того же смысла.
Доказательство.
1.Так как a > b и c > 0, то ac > bc – по свойству 3.
2.Так как с > d и b > 0, то cb > db – по свойству 3.
3. Итак, ac > bc, bc > bd. Тогда ac > bd - по свойству транзитивности, что и требовалось доказать.
Слайд 11Свойство 6.
Если а и b — неотрицательные числа и а
> b, то аn > Ьn, где n — любое натуральное число.
То есть, если обе части неравенства — неотрицательные числа, то их можно возвести в одну и ту же натуральную степень, сохранив знак неравенства.Дополнение:
Если n — нечетное число, то для любых чисел а и b из неравенства а > b следует неравенство того же смысла аn > bn.
Слайд 12Пример 1.
Пусть a и b - положительные числа и a
> b.
Доказать, что
Решение.
Рассмотрим разность
Имеем:
По условию, а, b, а - b — положительные числа. Значит,
- отрицательное число, т.е.
откуда следует, что
Слайд 13Пример 2.
Пусть а — положительное число.
Доказать, что
Решение.
Получили неотрицательное
число, значит,
Заметим, что
Слайд 14Пример 3.
Пусть а и b неотрицательные числа.
Доказать, что
Решение.
Составим
разность левой и правой частей неравенства. Имеем
Слайд 15В этом случае, число
называют средним арифметическим чисел а и b;
Число
называют средним геометрическим чисел а и b. Таким образом, среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Доказанное неравенство иногда называют неравенством Коши в честь французского математика XIX века Огюста Коши.
Замечание. Неравенство Коши имеет любопытное геометрическое истолкование. Пусть дан прямоугольный треугольник и пусть высота h, проведенная из вершины прямого угла, делит гипотенузу на отрезки а и b (рис. 116). В геометрии доказано, что
(так что не случайно для этого выражения ввели термин «среднее геометрическое»). А что такое ?
Это длина половины гипотенузы. Но из геометрии известно, что медиана m прямоугольного треугольника, проведенная из вершины прямого угла, как раз и равна половине гипотенузы. Таким образом, неравенство Коши означает, что медиана, проведенная к гипотенузе, т. е. , ,
не меньше высоты, проведенной к гипотенузе (т.е. ),
— очевидный геометрический факт (см. рис. 116).
Огюсте́н Луи́ Коши́


 , " alt="Строгие и нестрогие неравенства НеравенстваСтрогиеНестрогиеНеравенства отношений >, ">
, " alt="Строгие и нестрогие неравенства НеравенстваСтрогиеНестрогиеНеравенства отношений >, "> b и b >" alt="Свойства числовых неравенствСвойство 1. Если a > b и b > c, то a > cДоказательство. 1)">
b и b >" alt="Свойства числовых неравенствСвойство 1. Если a > b и b > c, то a > cДоказательство. 1)"> " alt="Обоснование свойства 1, при помощи числовой прямой Неравенство a > b означает, что на числовой">
" alt="Обоснование свойства 1, при помощи числовой прямой Неравенство a > b означает, что на числовой"> b, то a + c >" alt="Свойство 2. Если a > b, то a + c > b + c">
b, то a + c >" alt="Свойство 2. Если a > b, то a + c > b + c"> b и m > 0 , то" alt="Свойство 3.Если a > b и m > 0 , то a">
b и m > 0 , то" alt="Свойство 3.Если a > b и m > 0 , то a"> b и c > d, то a" alt="Свойство 4.Если a > b и c > d, то a + c > b + d.">
b и c > d, то a" alt="Свойство 4.Если a > b и c > d, то a + c > b + d.">
 " alt="Свойство 6.Если а и b — неотрицательные числа и а > b, то аn > Ьn, где n">
" alt="Свойство 6.Если а и b — неотрицательные числа и а > b, то аn > Ьn, где n"> " alt="Пример 1.Пусть a и b - положительные числа и a > b. Доказать, что">
" alt="Пример 1.Пусть a и b - положительные числа и a > b. Доказать, что">