Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема косинусов (9 класс)
Содержание
- 1. Теорема косинусов (9 класс)
- 2. Цели Изучить теорему косинусовВырабатывать навыки решения задач на применение теоремы косинусов
- 3. Изучение формулировки теоремы
- 4. Квадрат стороны треугольника равен сумме квадратов двух
- 5. Доказательство теоремы
- 6. хУАСВ(c;0)bacС(bcosA; bsinA)B
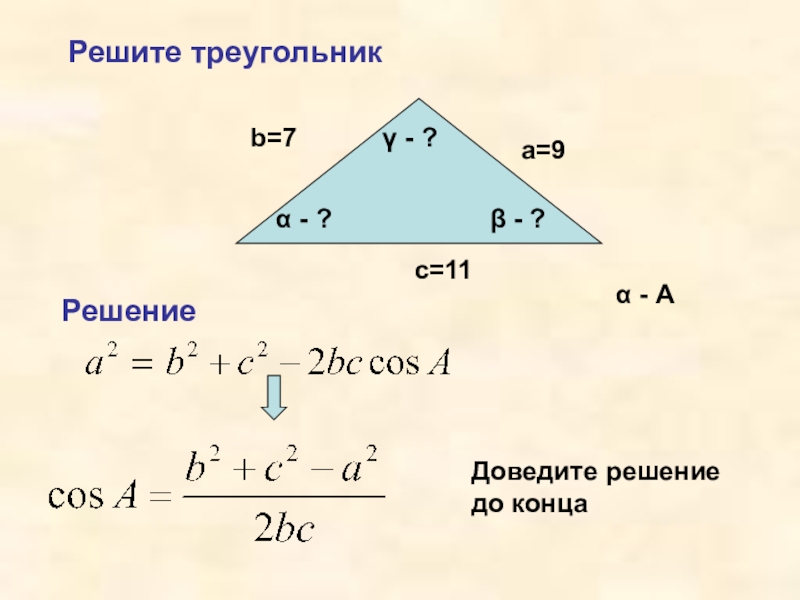
- 7. Решите треугольникb=7a=9c=11α - ?β - ?γ - ?Решениеα - АДоведите решение до конца
- 8. Утверждения, эквивалентные теореме косинусов для сферического треугольника,
- 9. Исторические сведенияАбу Абдаллах Мухаммад ибн Джабир ибн
- 10. Ал-Баттани провёл в Ракке и Дамаске между
- 11. Региомонта́н (лат. Regiomontanus, подлинное имя — Йоганн
- 12. Родился в 1540 году в Фонтене-ле-Конт французской
- 13. Благодаря связям матери и браку своей ученицы
- 14. При жизни Виета была издана только часть
- 15. Решить № 1025(г, д)
- 16. https://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E5%EC%E0_%EA%EE%F1%E8%ED%F3%F1%EE%E2https://ru.wikipedia.org/wiki/%D0%90%D0%BB-%D0%91%D0%B0%D1%82%D1%82%D0%B0%D0%BD%D0%B8https://ru.wikipedia.org/wiki/%D0%92%D0%B8%D0%B5%D1%82,_%D0%A4%D1%80%D0%B0%D0%BD%D1%81%D1%83%D0%B0https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B3%D0%B8%D0%BE%D0%BC%D0%BE%D0%BD%D1%82%D0%B0%D0%BD
- 17. Скачать презентанцию
Цели Изучить теорему косинусовВырабатывать навыки решения задач на применение теоремы косинусов
Слайды и текст этой презентации
Слайд 1Теорема косинусов
урок геометрии, 9 класс,
УМК Л.С. Атанасян
Автор: Лазарчук Владимир
Николаевич,
Мурманской областиСлайд 2Цели
Изучить теорему косинусов
Вырабатывать навыки решения задач на применение теоремы
косинусов
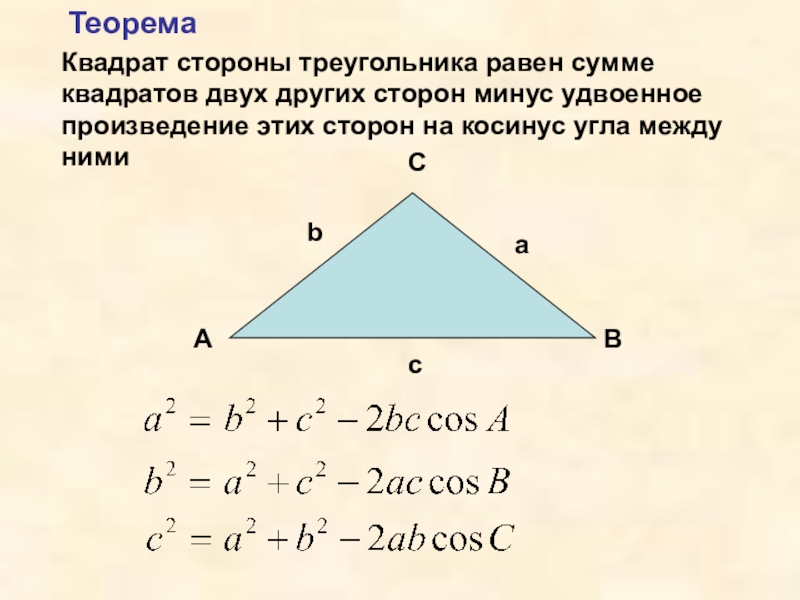
Слайд 4Квадрат стороны треугольника равен сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на косинус угла между ними
Теорема
А
b
a
c
С
B
Слайд 8Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях
математиков стран Средней Азии. Теорему косинусов для сферического треугольника в
привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» (по имени ал-Баттани).В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
Исторические сведения
Слайд 9Исторические сведения
Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Батта́ни (араб.
أبو عبد الله محمد بن جابر بن سنان الحراني الصابي
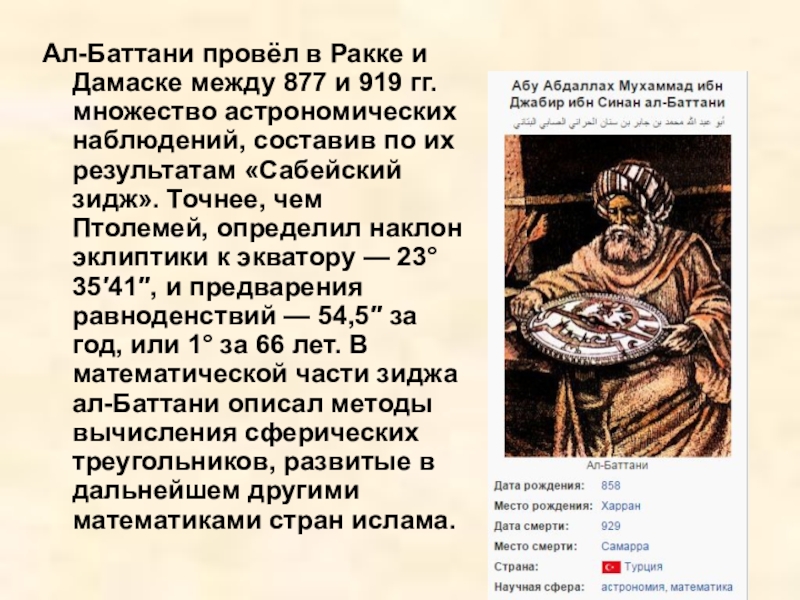
البتاني, Харран, 858 — Самарра, 929) — выдающийся средневековый астроном и математик, сабий по происхождению. В средневековой Европе был известен под латинизированным именем Albategnius.Слайд 10Ал-Баттани провёл в Ракке и Дамаске между 877 и 919
гг. множество астрономических наблюдений, составив по их результатам «Сабейский зидж».
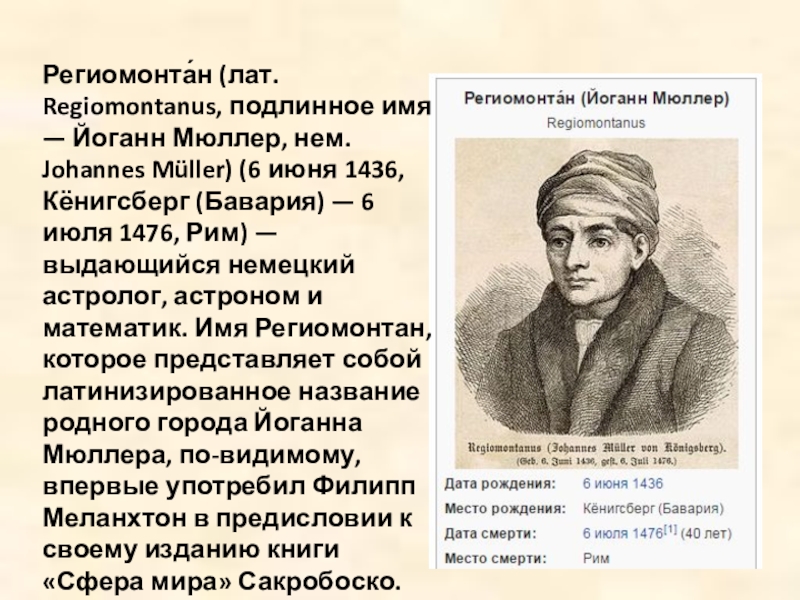
Точнее, чем Птолемей, определил наклон эклиптики к экватору — 23°35′41″, и предварения равноденствий — 54,5″ за год, или 1° за 66 лет. В математической части зиджа ал-Баттани описал методы вычисления сферических треугольников, развитые в дальнейшем другими математиками стран ислама.Слайд 11Региомонта́н (лат. Regiomontanus, подлинное имя — Йоганн Мюллер, нем. Johannes
Müller) (6 июня 1436, Кёнигсберг (Бавария) — 6 июля 1476,
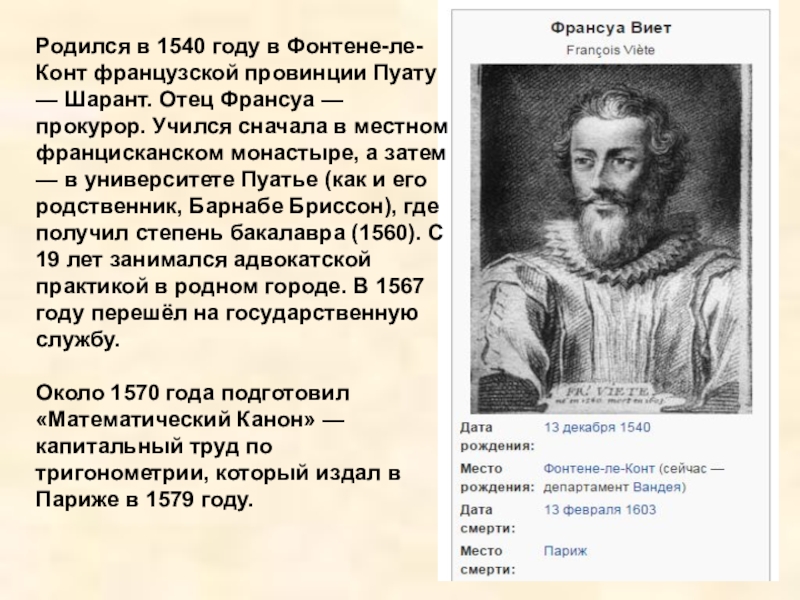
Рим) — выдающийся немецкий астролог, астроном и математик. Имя Региомонтан, которое представляет собой латинизированное название родного города Йоганна Мюллера, по-видимому, впервые употребил Филипп Меланхтон в предисловии к своему изданию книги «Сфера мира» Сакробоско.Слайд 12Родился в 1540 году в Фонтене-ле-Конт французской провинции Пуату —
Шарант. Отец Франсуа — прокурор. Учился сначала в местном францисканском
монастыре, а затем — в университете Пуатье (как и его родственник, Барнабе Бриссон), где получил степень бакалавра (1560). С 19 лет занимался адвокатской практикой в родном городе. В 1567 году перешёл на государственную службу.Около 1570 года подготовил «Математический Канон» — капитальный труд по тригонометрии, который издал в Париже в 1579 году.
Слайд 13Благодаря связям матери и браку своей ученицы с принцем де
Роганом, Виет сделал блестящую карьеру и стал советником сначала короля
Генриха III, а после его убийства — Генриха IV. По поручению Генриха IV Виет сумел расшифровать переписку испанских агентов во Франции, за что был даже обвинён испанским королём Филиппом II в использовании чёрной магии.Когда в результате придворных интриг Виет был на несколько лет отстранён от дел (1584—1588), он полностью посвятил себя математике. Изучил труды классиков (Кардано, Бомбелли, Стевина и др.). Итогом его размышлений стали несколько трудов, в которых Виет предложил новый язык «общей арифметики» — символический язык алгебры.
Слайд 14При жизни Виета была издана только часть его трудов. Главное
его сочинение — «Введение в аналитическое искусство» (1591), которое он
рассматривал как начало всеобъемлющего трактата, но продолжить не успел. Есть гипотеза, что учёный умер насильственной смертью. Сборник трудов Виета был издан посмертно (1646, Лейден) его голландским другом Ф. ван Схотеном.Слайд 16
https://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E5%EC%E0_%EA%EE%F1%E8%ED%F3%F1%EE%E2
https://ru.wikipedia.org/wiki/%D0%90%D0%BB-%D0%91%D0%B0%D1%82%D1%82%D0%B0%D0%BD%D0%B8
https://ru.wikipedia.org/wiki/%D0%92%D0%B8%D0%B5%D1%82,_%D0%A4%D1%80%D0%B0%D0%BD%D1%81%D1%83%D0%B0
https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B3%D0%B8%D0%BE%D0%BC%D0%BE%D0%BD%D1%82%D0%B0%D0%BD
Теги