Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку "Логарифмическая функция"
Содержание
- 1. Презентация к уроку "Логарифмическая функция"
- 2. ТЕМА УРОКА: ПОВТОРЕНИЕ «ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ В УРАВНЕНИЯХ».
- 3. УРОК ПОСТРОЕН ПО ЭТАПАМ:1-й Логарифмическая функция и
- 4. ДЖОН НЕПЕР (1550-1617) Шотландский математик – изобретатель
- 5. ПАЛОЧКИ НЕПЕРА НЕПЕР ПРЕДЛОЖИЛ В 1617 ГОДУ
- 6. Слово логарифм происходит от греческого слова (число)
- 7. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА. ГУНТЕР.В 1614 году шотландский математик
- 8. ОДА ЭКСПОНЕНТЕДве шкалы Гунтера – Вот чудо
- 9. 2-й «Потяни за ниточку» (теоретический)
- 10. НАЙДИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ, ИМЕЮЩИЕ СМЫСЛ: LOG3
- 11. НАЙТИ ВЕРНЫЕ РАВЕНСТВА: LOG2 8 = 3
- 12. Какой знак имеет функция у= LOG2 х на промежутке (0;1)
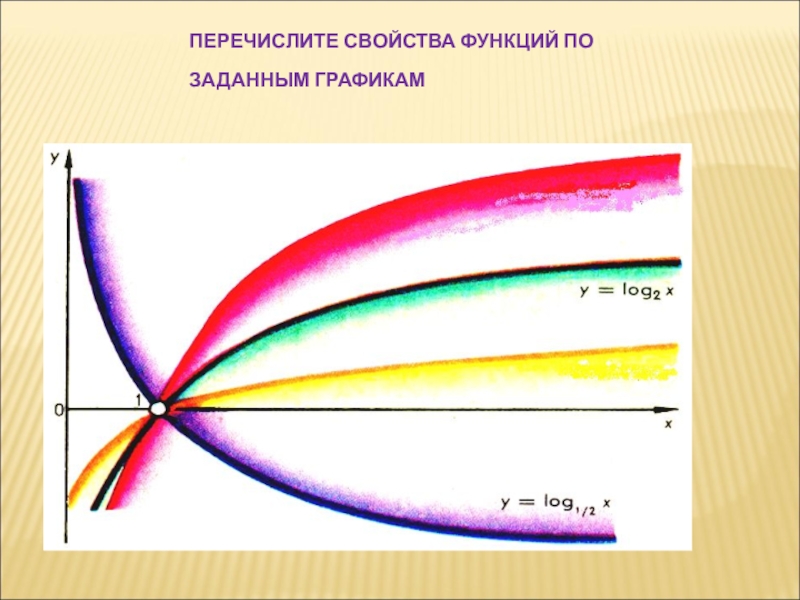
- 13. ПЕРЕЧИСЛИТЕ СВОЙСТВА ФУНКЦИЙ ПО ЗАДАННЫМ ГРАФИКАМ
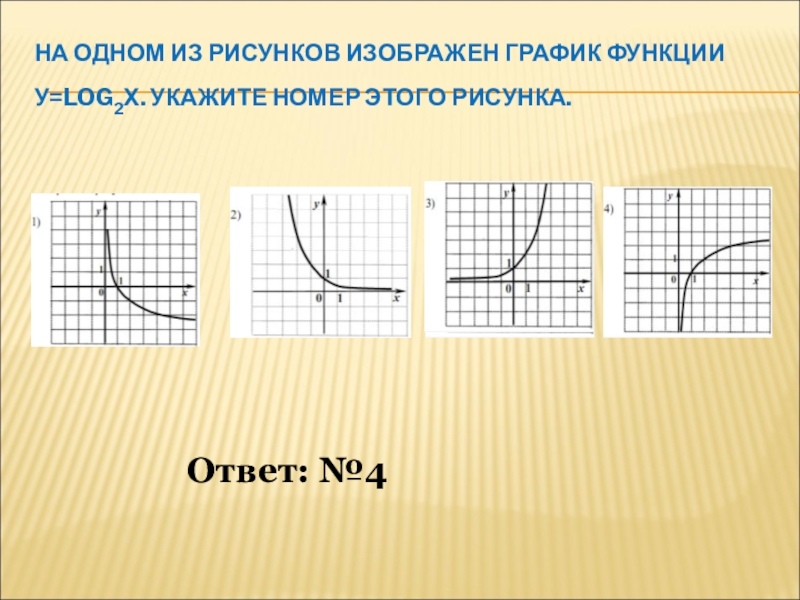
- 14. Ответ: №4НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ У=LOG2Х. УКАЖИТЕ НОМЕР ЭТОГО РИСУНКА.
- 15. НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ У= LOG2(5 – 3X)Ответ: №4
- 16. Логарифмическая «комедия 2>3»
- 17. «ЛОГАРИФМИЧЕСКИЕ ДИКОВИНКИ»Вычислить: LOGх у LOGу х
- 18. ЛЮБОЕ ЧИСЛО– ТРЕМЯ ДВОЙКАМИЛюбое целое положительное число можно представить с помощью трех двоек и математических символов.*
- 19. «РАССКАЖИ МНЕ, И Я ЗАБУДУ, ПОКАЖИ
- 20. ЛОГАРИФМИЧЕСКИЕ ДИКОВИНКИВычислить
- 21. 5 – тремя двойками
- 22. 5-й «Видит око, да ум ещё
- 23. 6-й «На приз Непера» ( самостоятельная работа)Учебное пособие «математика подготовка к ЕГЭ-2012»Стр.285 № 977, 988
- 24. 7-й Подведение итогов урока, выставление оценок, задание
- 25. Скачать презентанцию
ТЕМА УРОКА: ПОВТОРЕНИЕ «ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ В УРАВНЕНИЯХ».
Слайды и текст этой презентации
Слайд 3УРОК ПОСТРОЕН ПО ЭТАПАМ:
1-й Логарифмическая функция и её приложение (историческая
справка)
2-й «Потяни за ниточку» (теоретический)
3-й «Логарифмическая комедия» (найдите ошибку,
кто быстрее)4-й Любое число – тремя «2»
5-й «Видит око, да ум ещё дальше» (задание на прямое применение свойств логарифмической функции)
6-й «На приз Непера» ( самостоятельная работа)
7-й Подведение итогов урока, выставление оценок, задание на дом.
Слайд 4ДЖОН НЕПЕР
(1550-1617)
Шотландский математик –
изобретатель логарифмов.
В 1590-х
годах пришел к идее
логарифмических вычислений
и составил первые
таблицы логарифмов, однако свой знаменитый
“Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Слайд 5ПАЛОЧКИ НЕПЕРА
НЕПЕР ПРЕДЛОЖИЛ
В 1617 ГОДУ ДРУГОЙ
(НЕ ЛОГАРИФМИЧЕСКИЙ)
СПОСОБ
ПЕРЕМНОЖЕНИЯ ЧИСЕЛ.
ИНСТРУМЕНТ, ПОЛУЧИВШИЙ
НАЗВАНИЕ ПАЛОЧКИ (ИЛИ КОСТЯШКИ) НЕПЕРА,
СОСТОЯЛ
ИЗ ТОНКИХ ПЛАСТИН, ИЛИ БЛОКОВ. КАЖДАЯ СТОРОНА БЛОКА НЕСЕТ ЧИСЛА, ОБРАЗУЮЩИЕ
МАТЕМАТИЧЕСКУЮ ПРОГРЕССИЮ. МАНИПУЛЯЦИИ С
БЛОКАМИ ПОЗВОЛЯЮТ ИЗВЛЕКАТЬ КВАДРАТНЫЕ И
КУБИЧЕСКИЕ КОРНИ, А ТАКЖЕ УМНОЖАТЬ И ДЕЛИТЬ
БОЛЬШИЕ ЧИСЛА.
Слайд 6
Слово логарифм происходит от греческого слова (число) и (отношение) и
переводится, следовательно, как отношение чисел. Выбор изобретателем логарифмов Дж. Непером
такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое — геометрическим.
Слайд 7ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА. ГУНТЕР.
В 1614 году шотландский математик Джон Непер изобрел
таблицы логарифмов. Принцип их заключался в том, что каждому числу
соответствует свое специальное число - логарифм.Логарифмы очень упрощают деление и умножение.
Например, для умножения двух чисел складывают их логарифмы, результат находят в таблице логарифмов.
В дальнейшем им была изобретена логарифмическая
линейка, которой пользовались до 70-х годов нашего века.
Слайд 8ОДА ЭКСПОНЕНТЕ
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая
линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные
искусства питаются ею.Разве музыкальная гамма не есть
Набор передовых логарифмов?
Английский поэт Э.Брилл
Слайд 14
Ответ: №4
НА ОДНОМ ИЗ РИСУНКОВ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ У=LOG2Х. УКАЖИТЕ
НОМЕР ЭТОГО РИСУНКА.
3»" alt="Логарифмическая «комедия 2>3»">
Слайд 18ЛЮБОЕ ЧИСЛО– ТРЕМЯ ДВОЙКАМИ
Любое целое положительное число можно представить с
помощью трех двоек и математических символов.
*
Слайд 19«РАССКАЖИ МНЕ, И Я ЗАБУДУ, ПОКАЖИ МНЕ, И Я ЗАПОМНЮ, ДАЙ
МНЕ СДЕЛАТЬ САМОМУ, И Я ПОЙМУ»
О. ХАЙЯМ
Слайд 22
5-й «Видит око, да ум ещё дальше»
(задание на
прямое применение свойств логарифмической функции) – на доске
Слайд 23
6-й «На приз Непера»
( самостоятельная работа)
Учебное пособие
«математика подготовка
к ЕГЭ-2012»
Стр.285 № 977, 988
Слайд 24
7-й Подведение итогов урока, выставление оценок, задание на дом.
Учебное пособие
«математика подготовка к ЕГЭ-2012 стр.290 №1056, 1060
