Слайд 2Содержание
1. Основные аксиомы и определения.
2. Взаимное расположение точек,
прямых и плоскостей в пространстве.
3. Взаимное расположение двух прямых в
пространстве.
4. Параллельность прямой и плоскости.
5. Параллельные плоскости.
66. Перпендикулярность прямой и плоскости.
7. Двугранный и трехгранный углы.
8. Перпендикулярность плоскостей.
9. Теоремы стереометрии.
10. Индивидуальные задания.
11. Тестовые задания.
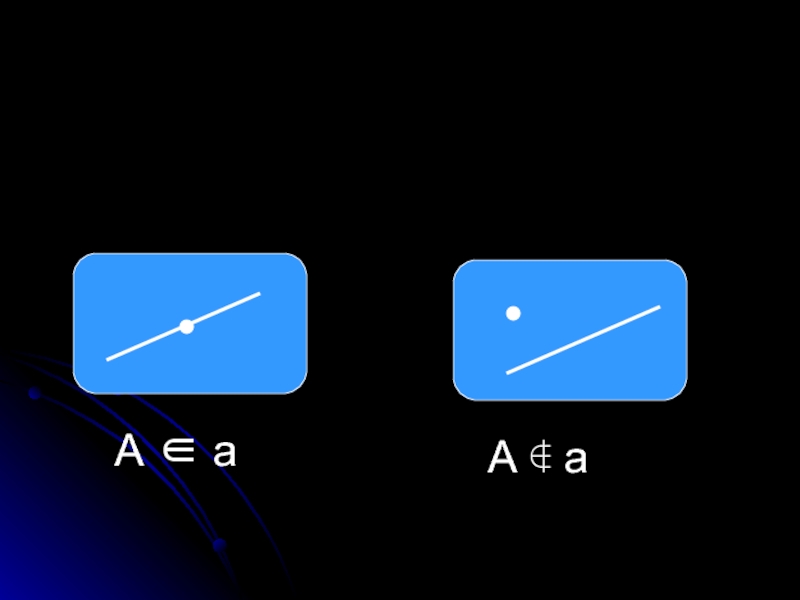
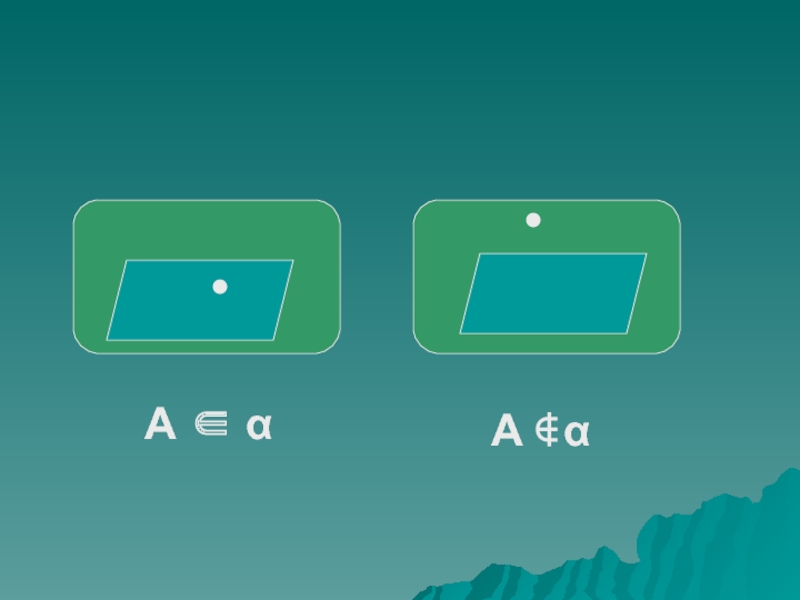
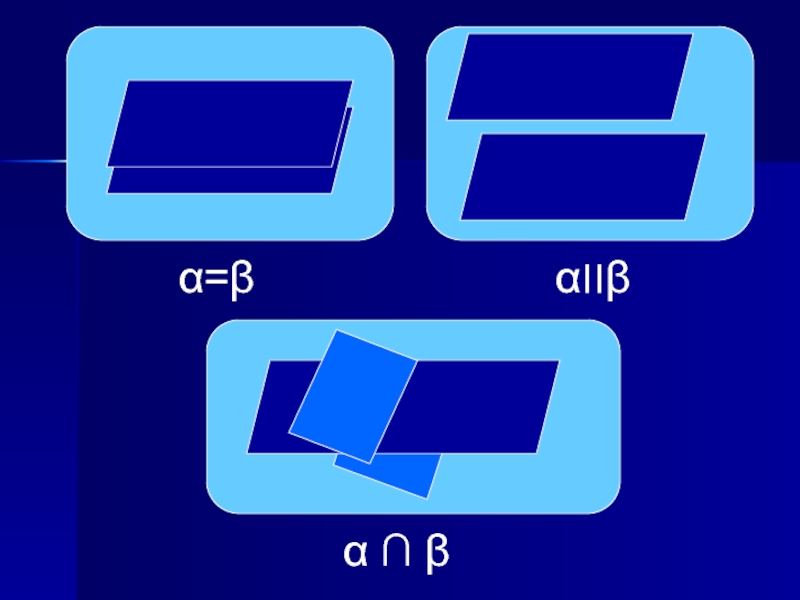
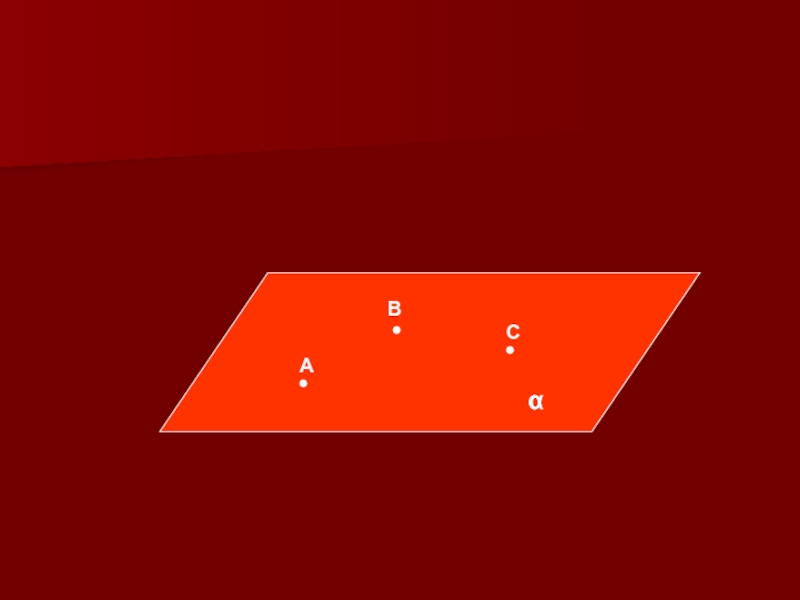
Слайд 3Взаимное расположение точек, прямых и плоскостей в простанстве
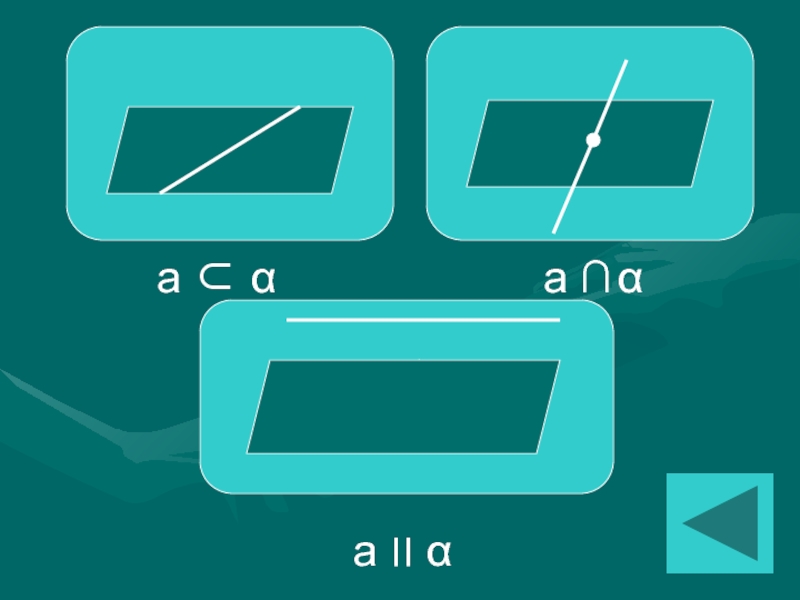
Слайд 6
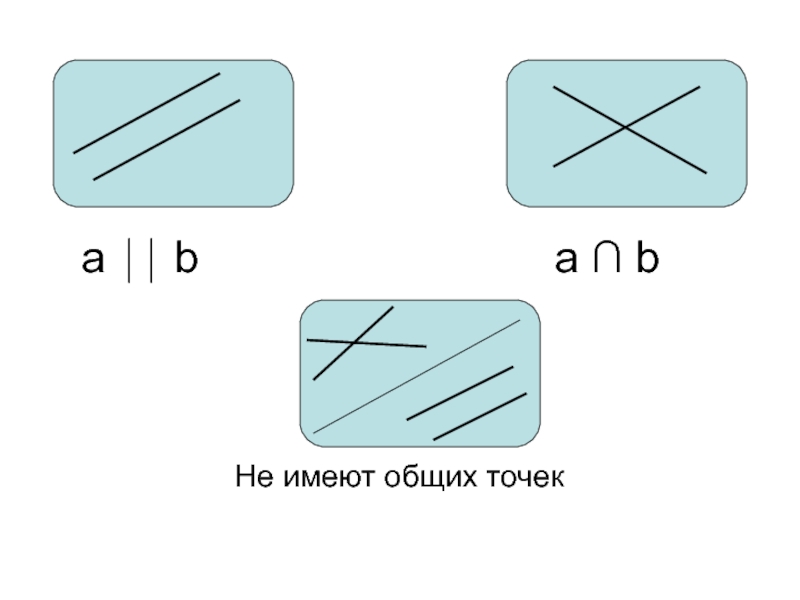
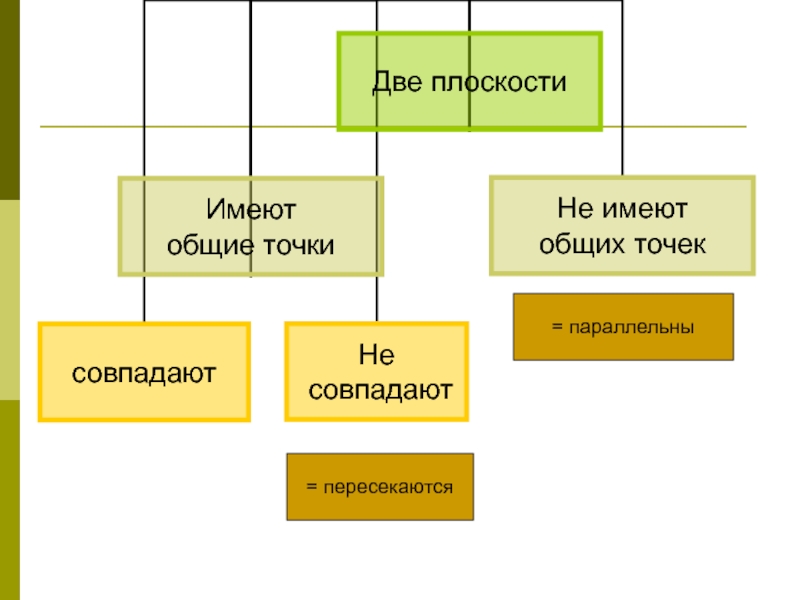
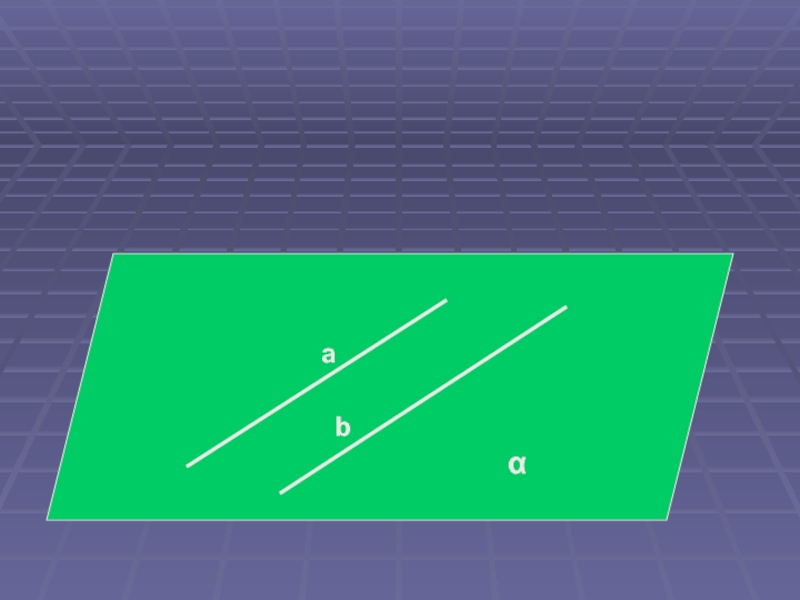
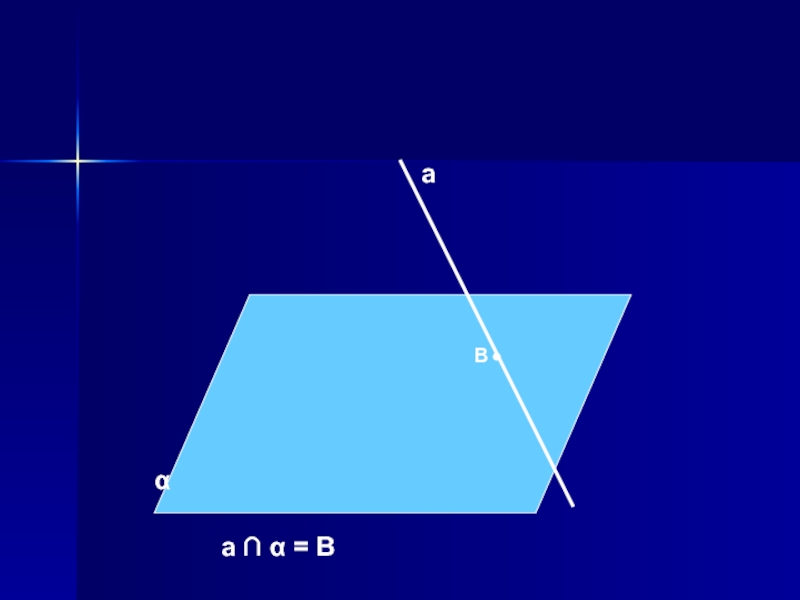
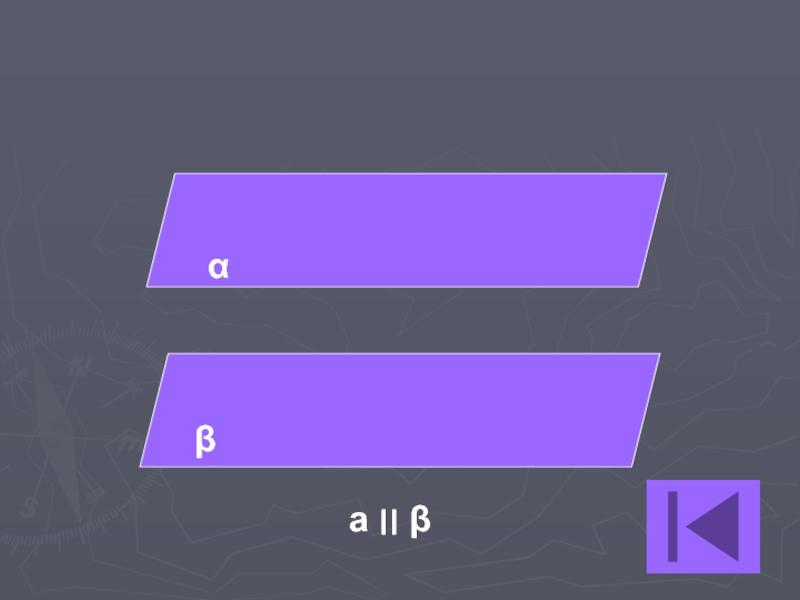
a ⏐⏐ b
a ∩ b
Не имеют общих точек
Слайд 9
Взаимное расположение двух прямых в пространстве
Слайд 10
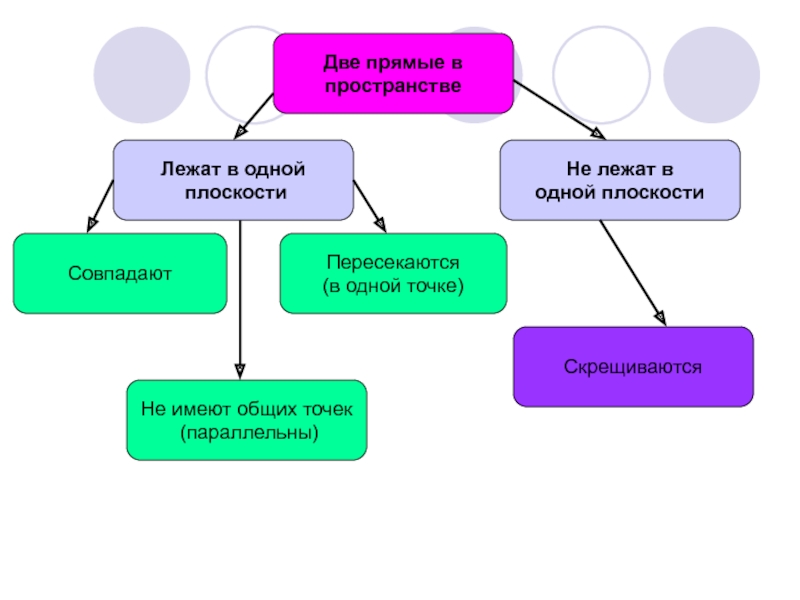
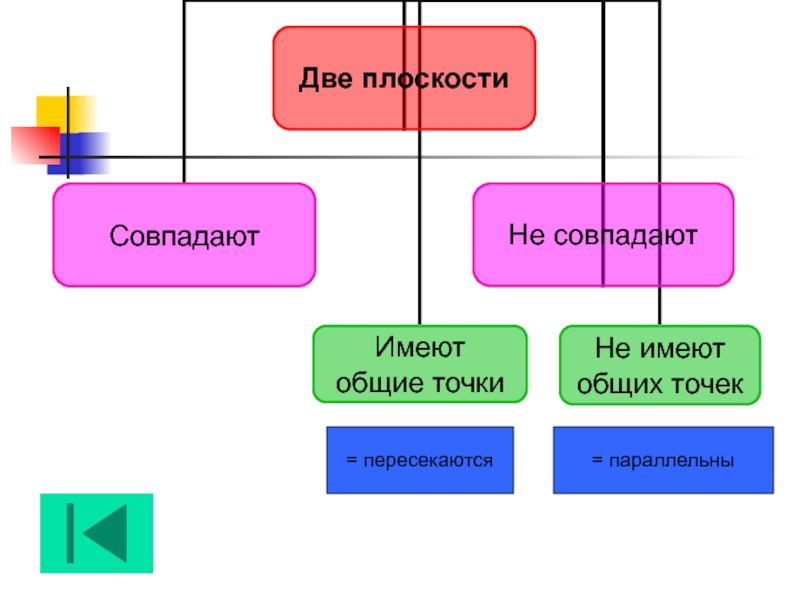
Две прямые в
пространстве
Лежат в одной
плоскости
Совпадают
Не лежат в
одной
плоскости
Не имеют общих точек
(параллельны)
Пересекаются
(в одной точке)
Скрещиваются
Слайд 11
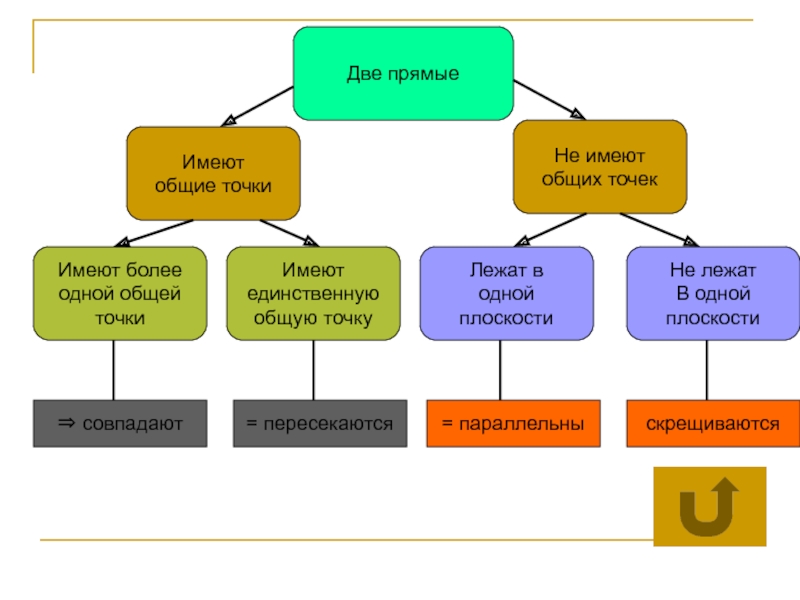
Имеют
единственную
общую точку
Имеют более
одной общей
точки
Лежат в
одной
плоскости
Не лежат
В одной
плоскости
Имеют
общие точки
Не имеют
общих точек
Две
прямые
⇒ совпадают
= пересекаются
= параллельны
скрещиваются
Слайд 12
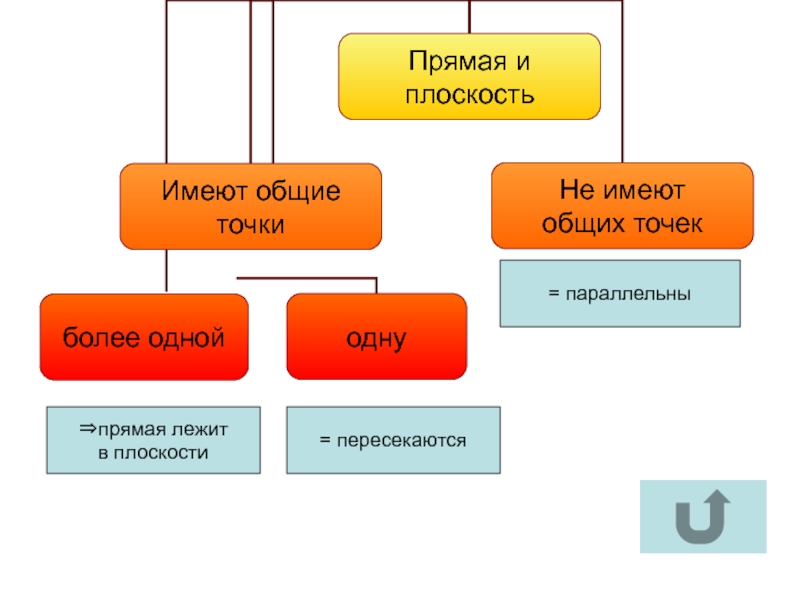
Параллельность прямой и плоскости
Слайд 13
⇒прямая лежит
в плоскости
= пересекаются
= параллельны
Слайд 18
Через любые три точки, не лежащие
на одной прямой, проходит
одна и только одна плоскость
Слайд 20
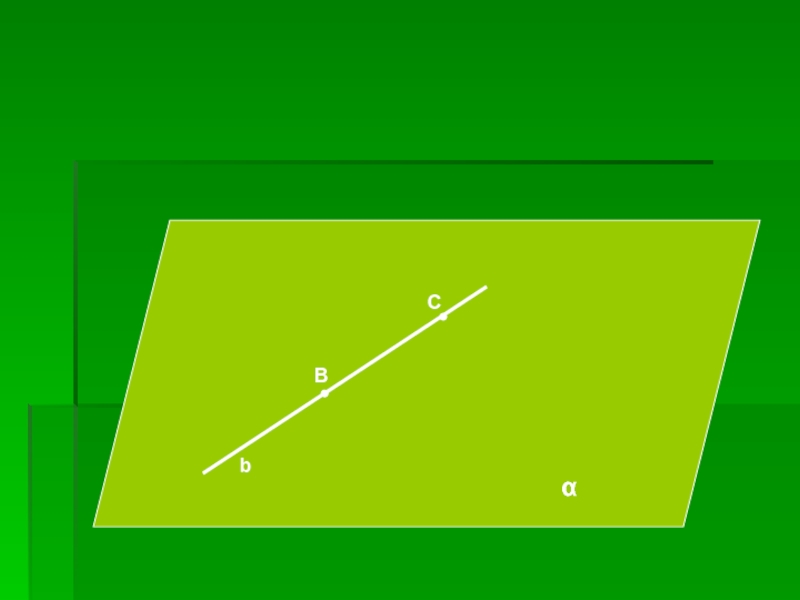
Если две точки прямой лежат в плоскости, то и вся
прямая лежит в этой плоскости.
Слайд 22
Прямая называется
параллельной плоскости,
а плоскость –
параллельной прямой,
если
они не имеют общих точек.
Слайд 24
Две прямые, имеющие только одну общую точку, называются пересекающимися
Слайд 26Две прямые, лежащие в одной плоскости и не имеющие общих
точек, называются параллельными.
Слайд 28
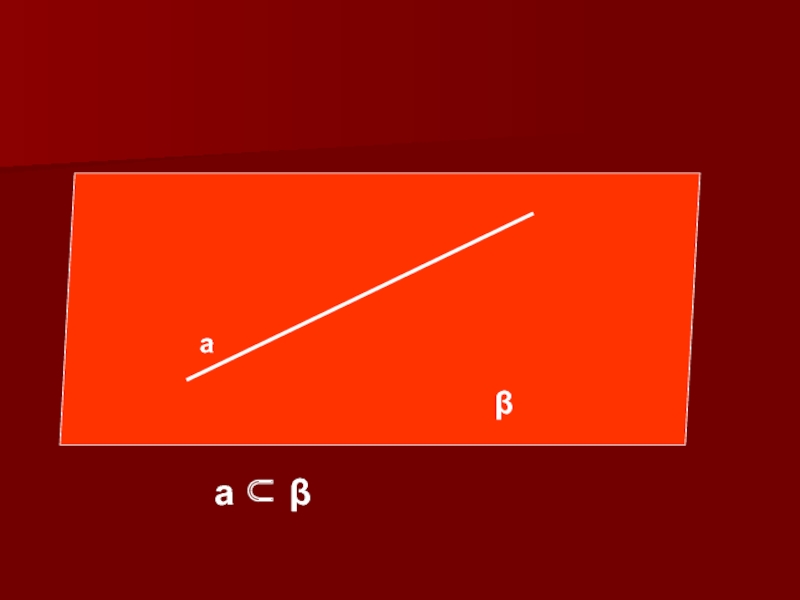
Прямая, все точки которой принадлежат плоскости, называется прямой,
лежащей в
этой плоскости.
Слайд 30
Прямая пересекает плоскость, если у них есть только одна общая
точка.
Слайд 32
Две плоскости, не имеющие общих точек, называются параллельными
Слайд 34
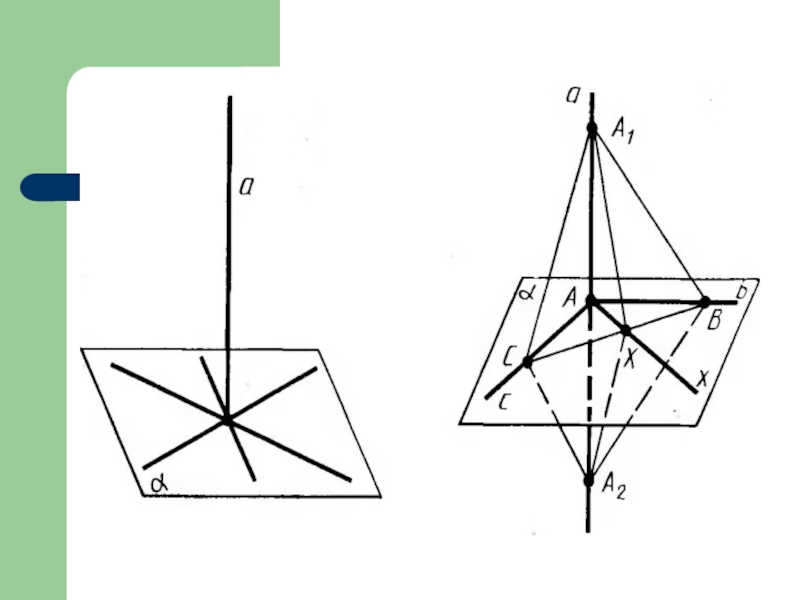
Прямая называется перпендикулярной плоскости (а плоскость прямой), если прямая перпендикулярна
любой прямой лежащей в этой плоскости.
Слайд 35
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Если прямая перпендикулярна двум пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна данной плоскости.
Слайд 37
СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ
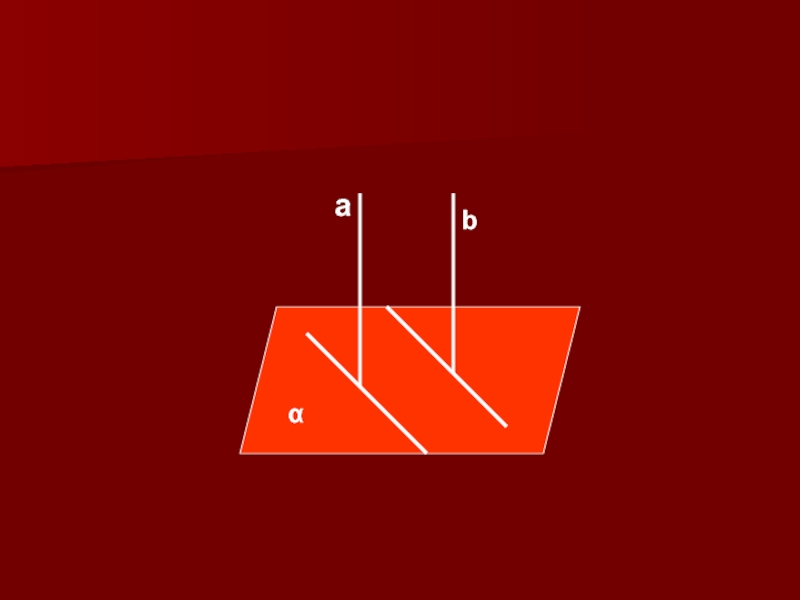
Если плоскость перпендикулярна одной из двух
параллельных прямых, то она перпендикулярна и другой.
Слайд 39
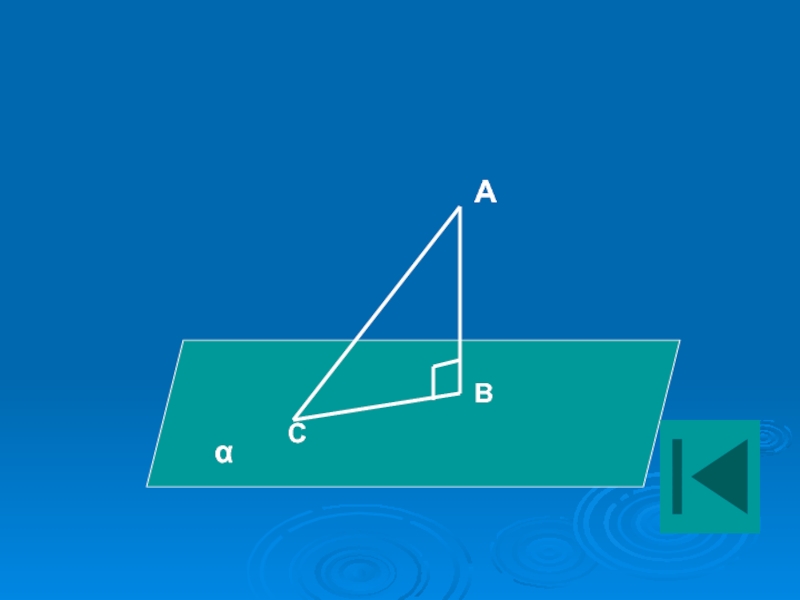
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Перпендикуляром, опущенным из данной точки на данную плоскость,
называется отрезок, соединяющий данную точку с точкой плоскости и лежащий
на прямой, перпендикулярной плоскости.
Слайд 40
Наклонной, проведенной из данной точки к данной плоскости, называется любой
отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром
к плоскости.
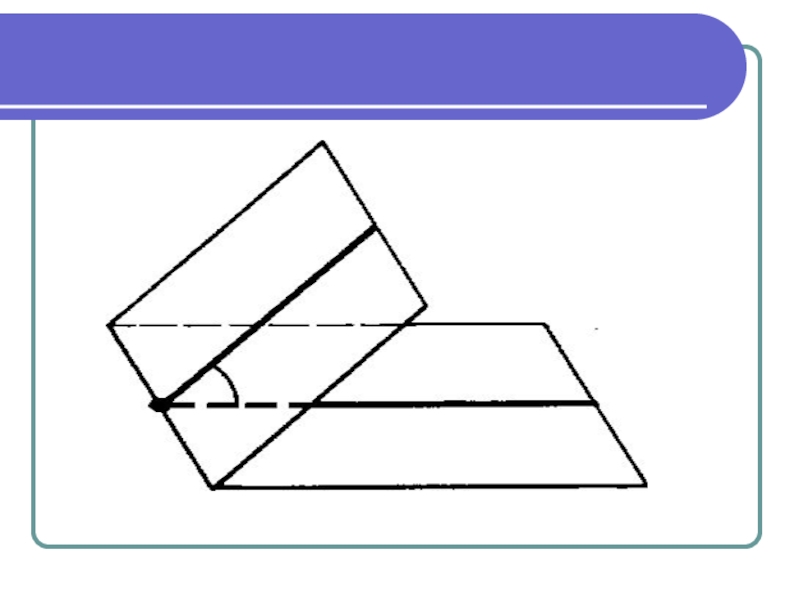
Слайд 42
Двугранным углом
называется фигура, образованная двумя полуплоскостями с общей ограничивающей
их прямой. Полуплоскости называются гранями, а ограничивающая их прямая —
ребром двугранного угла.
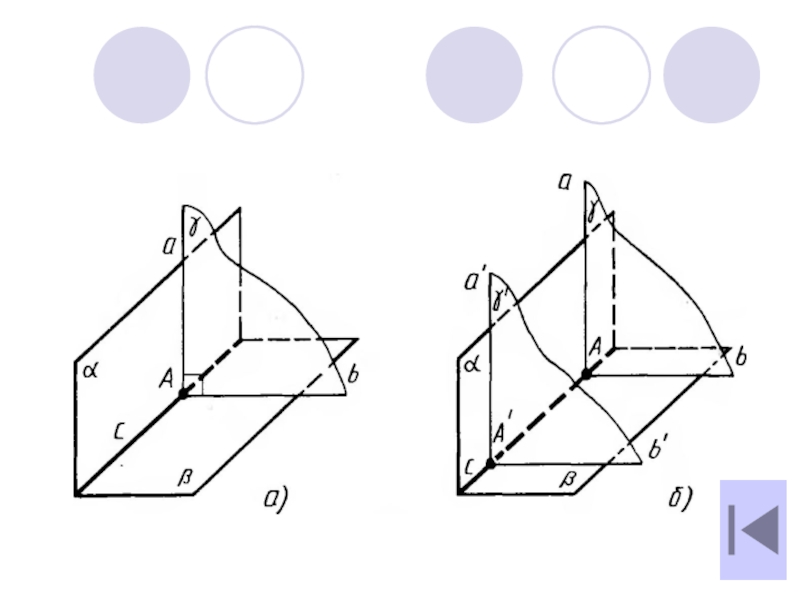
Слайд 44
Линейным углом двугранного
угла называется пересечение этого двугранного угла и
плоскости перпендикулярной его ребру.
Слайд 45
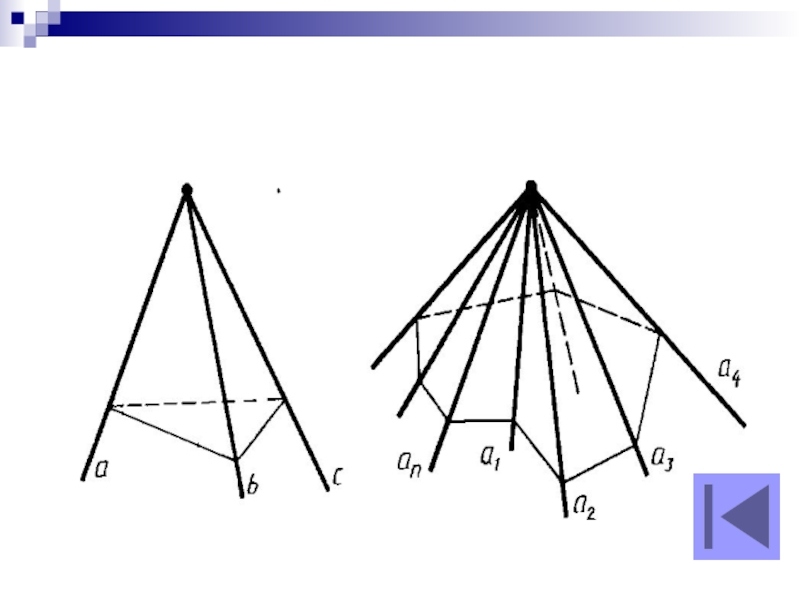
Трехгранным углом (аbс) называется фигура, составленная из трех плоских углов
(аb), (bс) и (ас). Эти углы называются гранями трехгранного угла,
а их стороны — ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Слайд 47
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная
прямой пересечения этих плоскостей, пересекает их по
перпендикулярным прямым.
Слайд 48
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ
Если плоскость проходит через прямую, перпендикулярную другой плоскости,
то эти плоскости перпендикулярны.
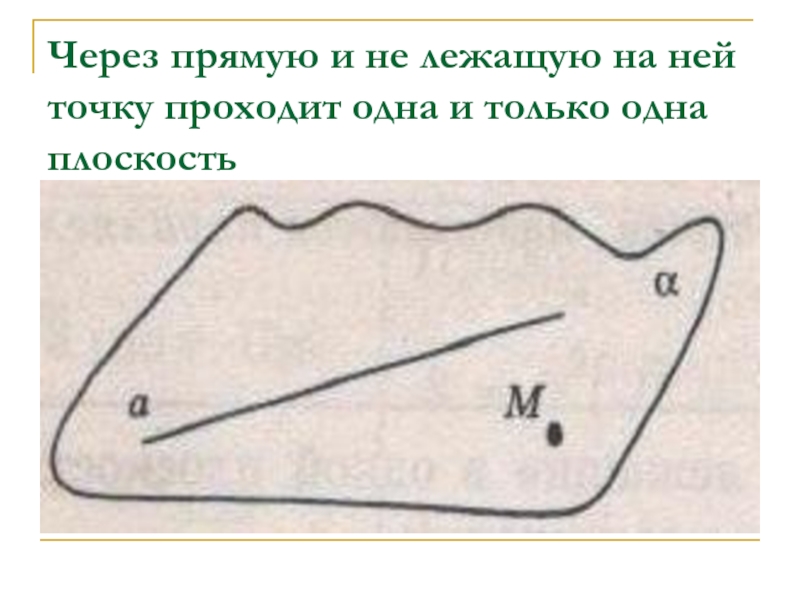
Слайд 51Через прямую и не лежащую на ней точку проходит одна
и только одна плоскость
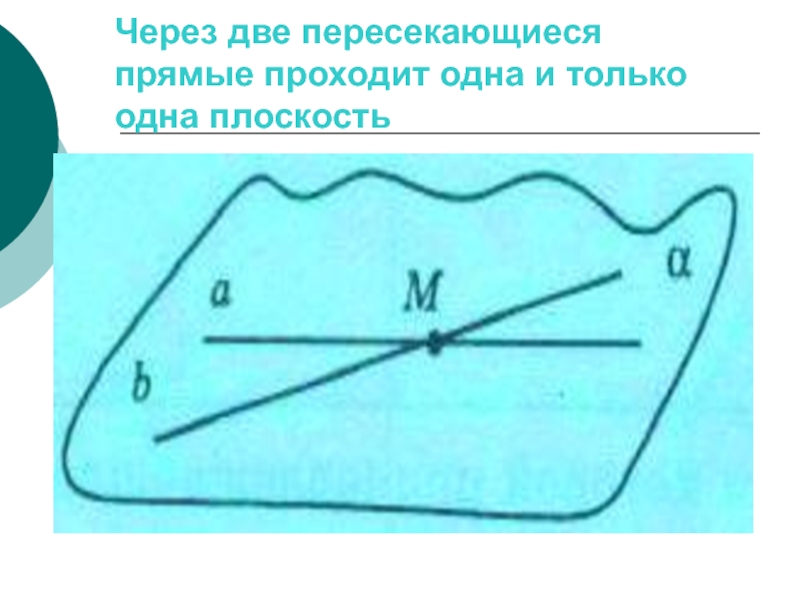
Слайд 52Через две пересекающиеся прямые проходит одна и только одна плоскость
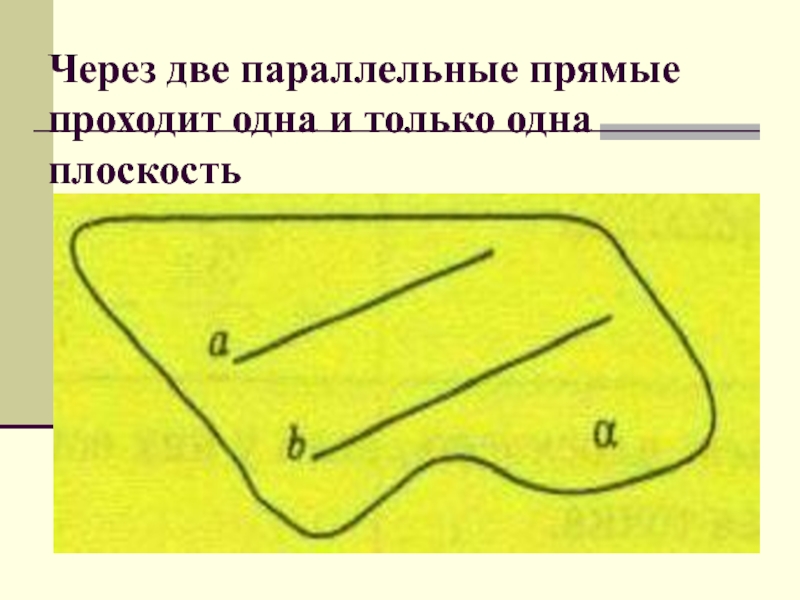
Слайд 53Через две параллельные прямые проходит одна и только одна плоскость
Слайд 54
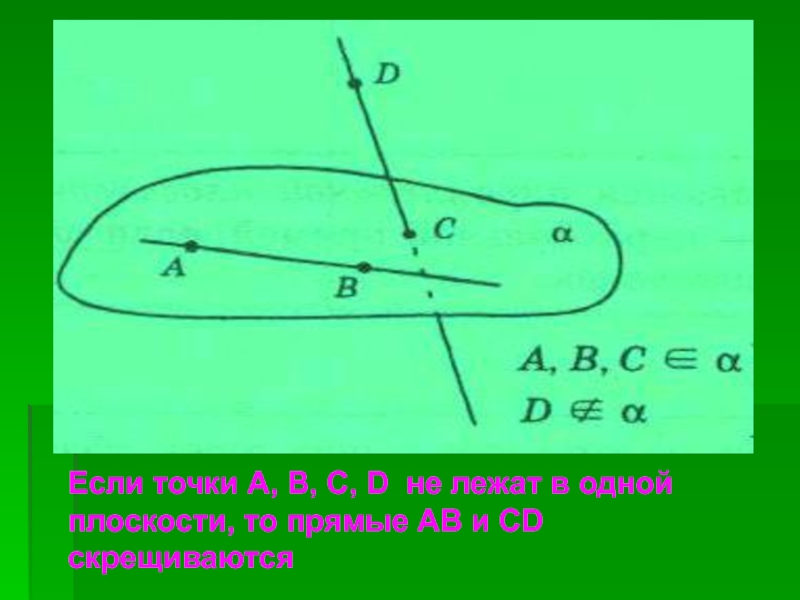
Если точки A, B, C, D не лежат в одной
плоскости, то прямые AB и CD скрещиваются
Слайд 55
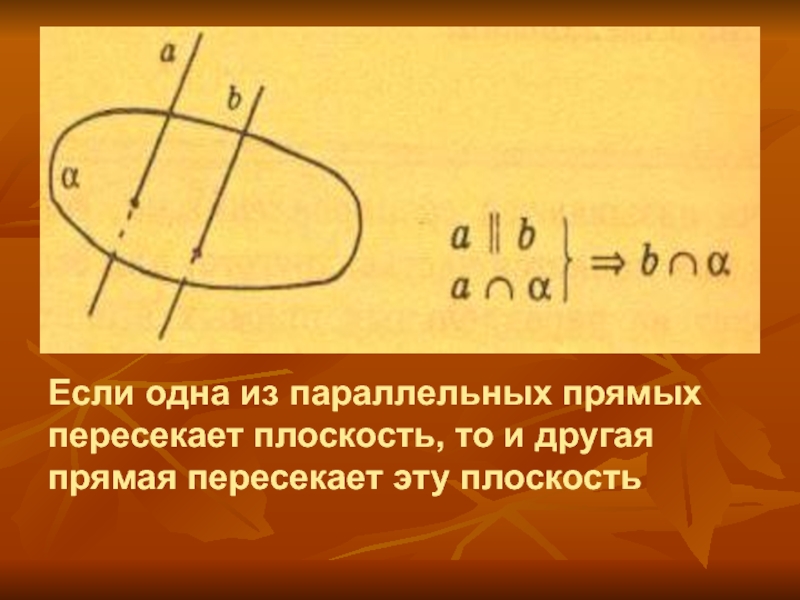
Если одна из параллельных прямых пересекает плоскость, то и другая
прямая пересекает эту плоскость
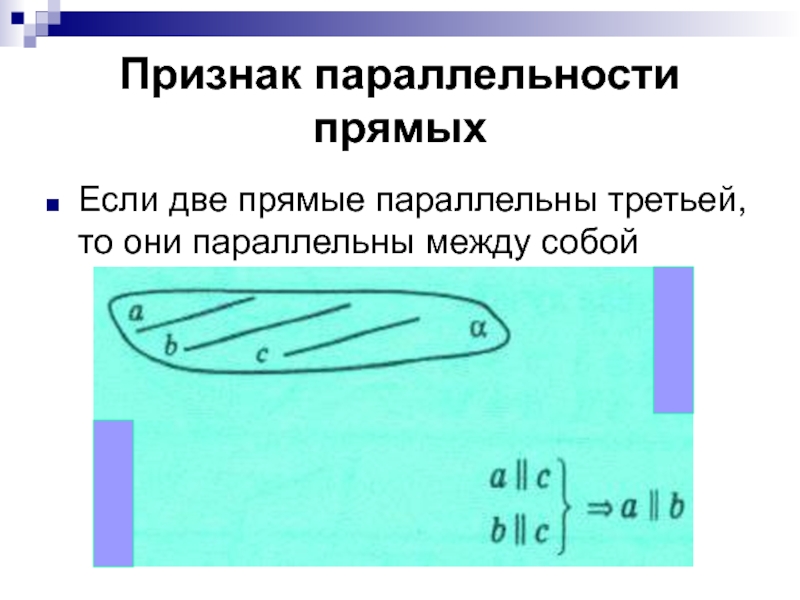
Слайд 56Признак параллельности прямых
Если две прямые параллельны третьей, то они параллельны
между собой
Слайд 57
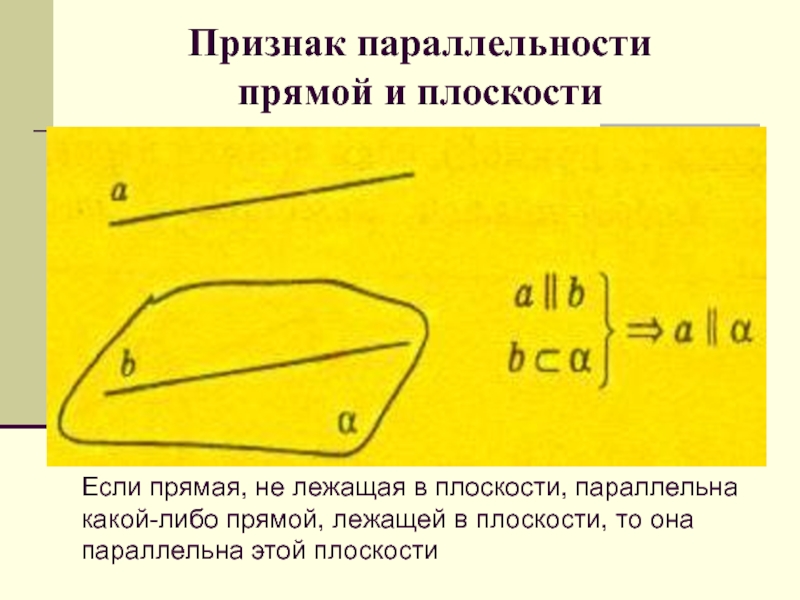
Признак параллельности
прямой и плоскости
Если прямая, не лежащая в плоскости,
параллельна какой-либо прямой, лежащей в плоскости, то она параллельна этой
плоскости
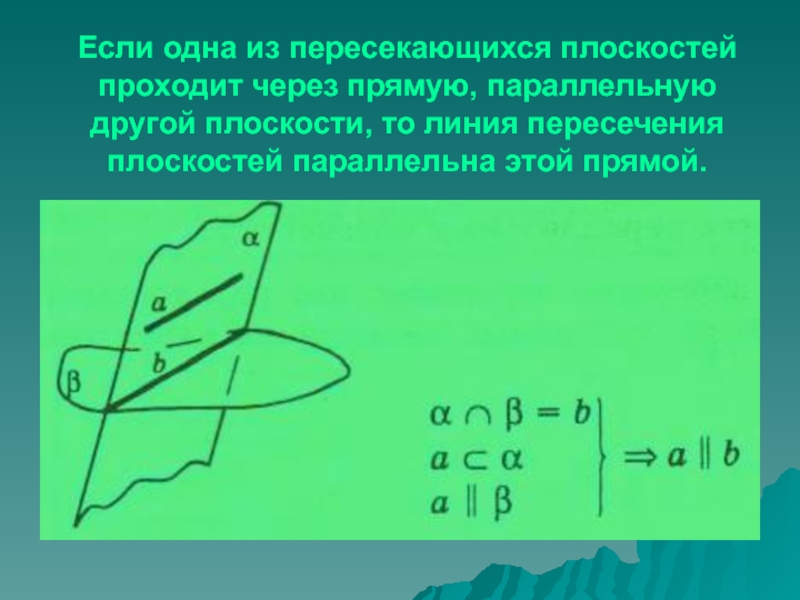
Слайд 58Если одна из пересекающихся плоскостей проходит через прямую, параллельную другой
плоскости, то линия пересечения плоскостей параллельна этой прямой.
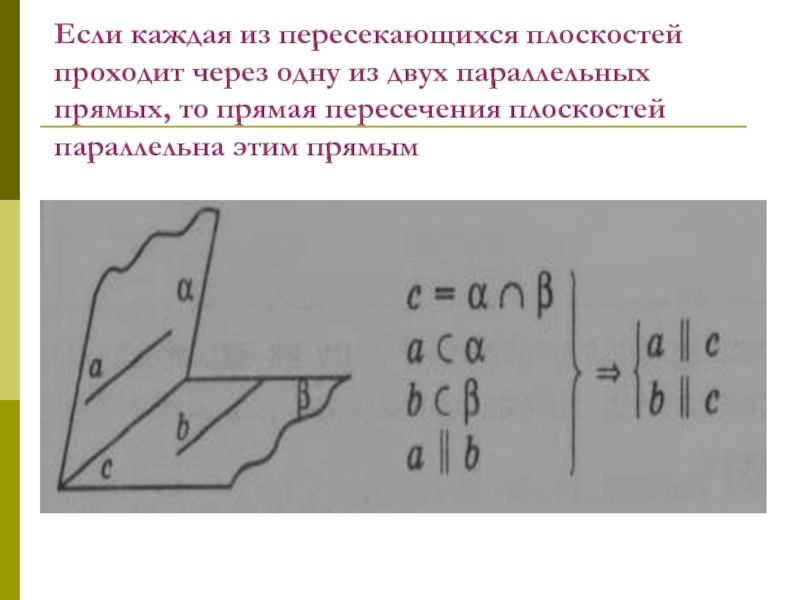
Слайд 59Если каждая из пересекающихся плоскостей проходит через одну из двух
параллельных прямых, то прямая пересечения плоскостей параллельна этим прямым
Слайд 60Если две пересекающиеся плоскости пересечены третьей плоскостью по параллельным прямым,
то линия их пересечения параллельна этим прямым
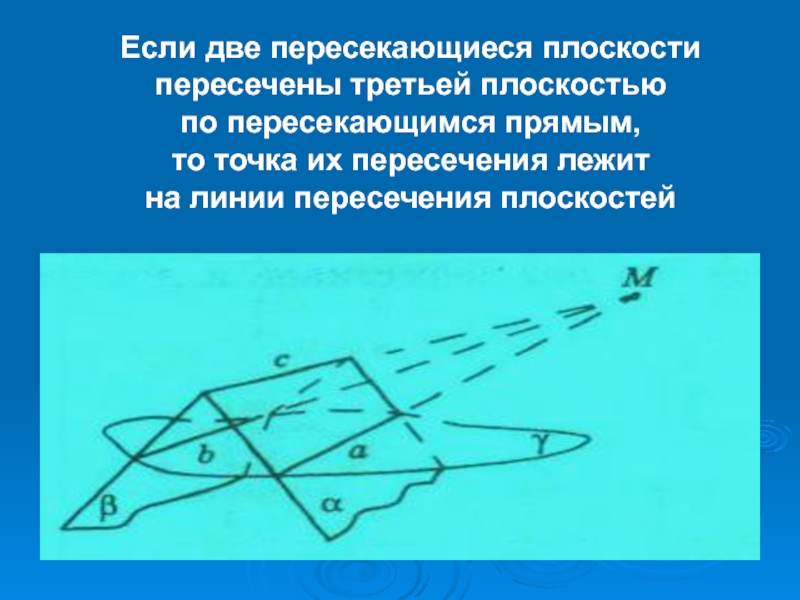
Слайд 61Если две пересекающиеся плоскости пересечены третьей плоскостью
по пересекающимся прямым,
то точка их пересечения лежит
на линии пересечения плоскостей
Слайд 62
Признаки параллелельности плоскостей
Слайд 63
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся
прямым другой плоскости, то эти плоскости параллельны
Слайд 64
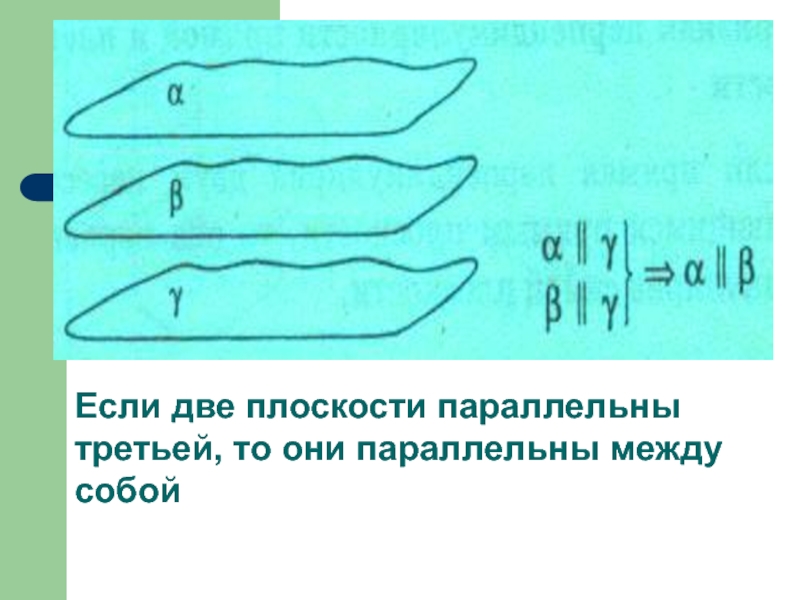
Если две плоскости параллельны третьей, то они параллельны между собой
Слайд 65
Свойства параллельных плоскостей
Слайд 66
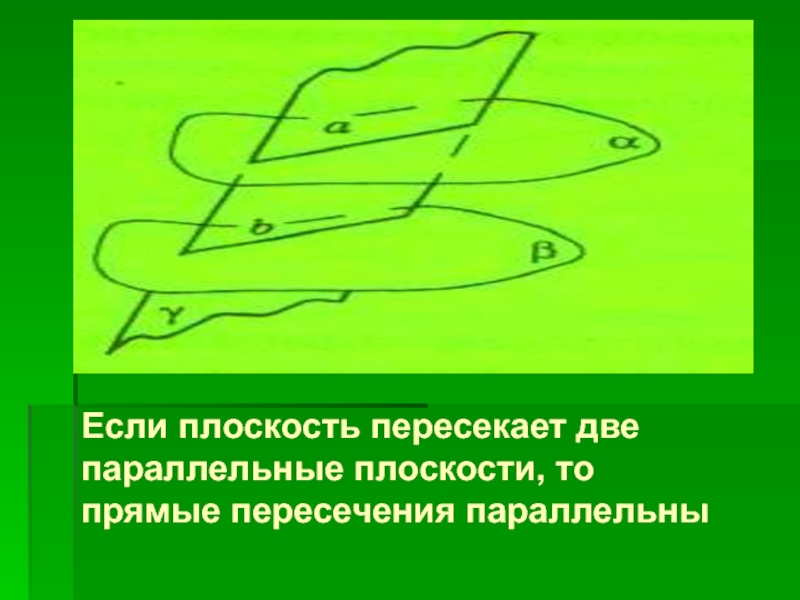
Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллельны
Слайд 67
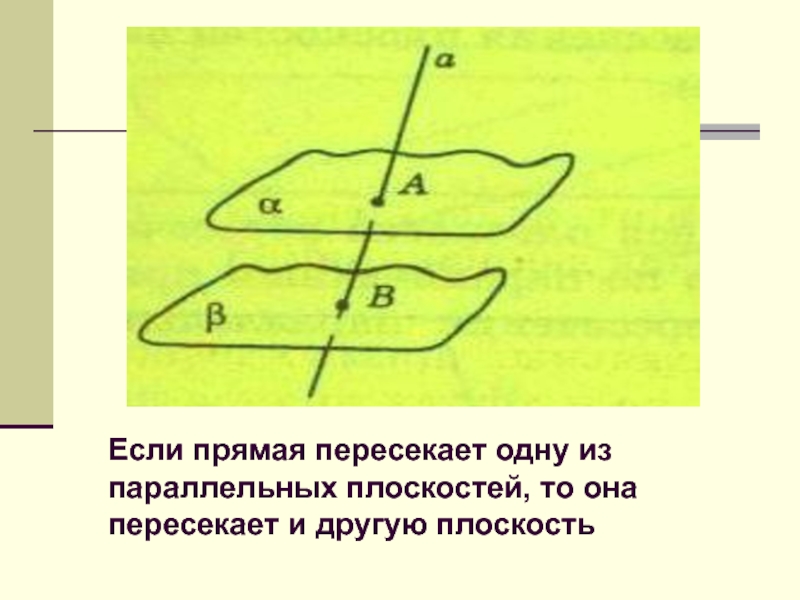
Если прямая пересекает одну из параллельных плоскостей, то она пересекает
и другую плоскость
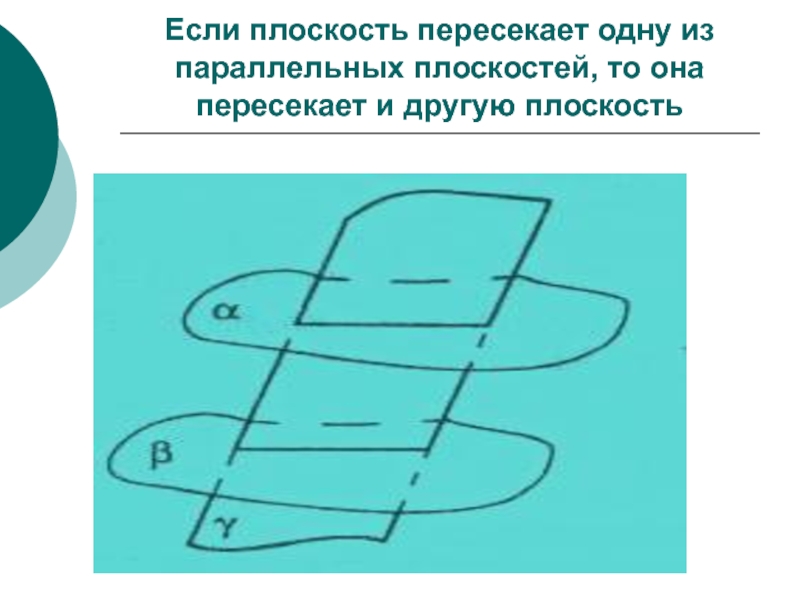
Слайд 68Если плоскость пересекает одну из параллельных плоскостей, то она пересекает
и другую плоскость
Слайд 69
Через точку, не лежащую на плоскости, можно провести одну и
только одну плоскость, параллельную данной
Слайд 70
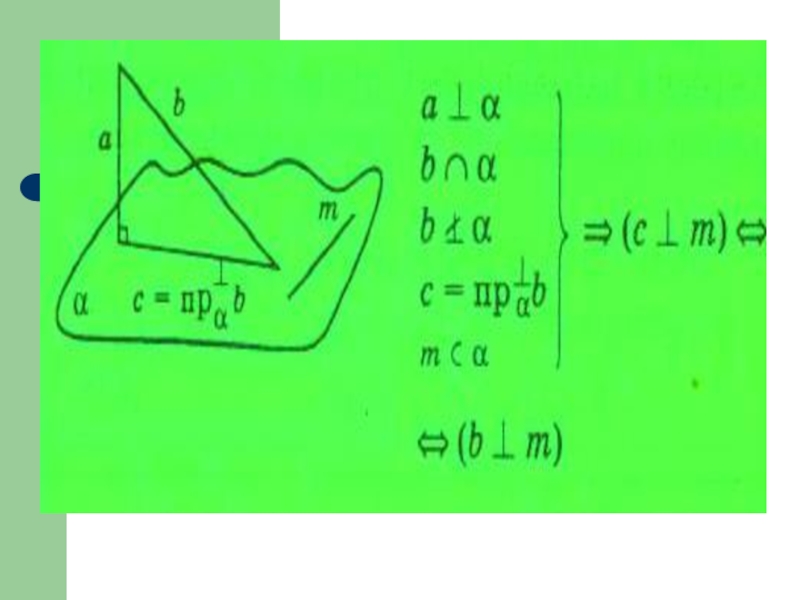
Если (ортогональная) проекция наклонной перпендикулярна прямой на плоскости, то и
сама наклонная перпендикулярна этой прямой.
Если наклонная перпендикулярна некоторой прямой плоскости,
то и (ортогональная) проекция наклонной на эту плоскость перпендикулярна этой прямой.
Теорема о трех перпендикулярах
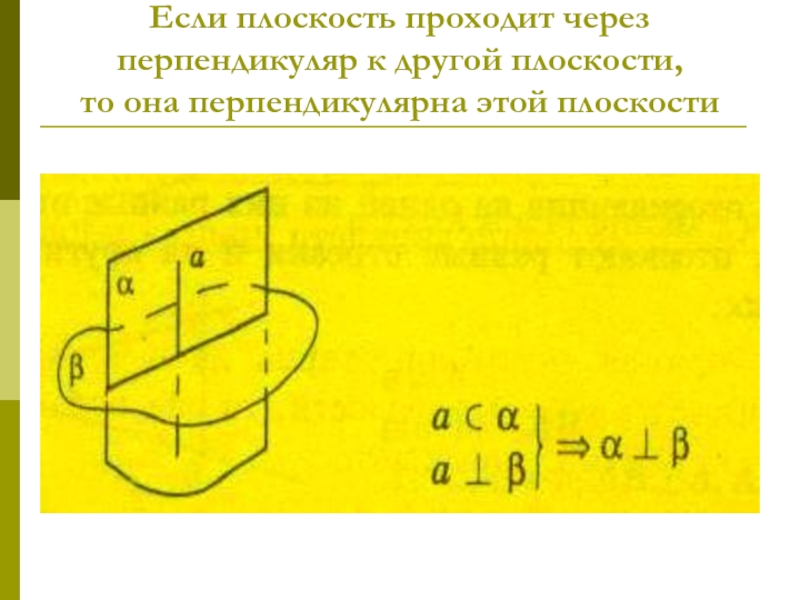
Слайд 72Если плоскость проходит через перпендикуляр к другой плоскости,
то она
перпендикулярна этой плоскости
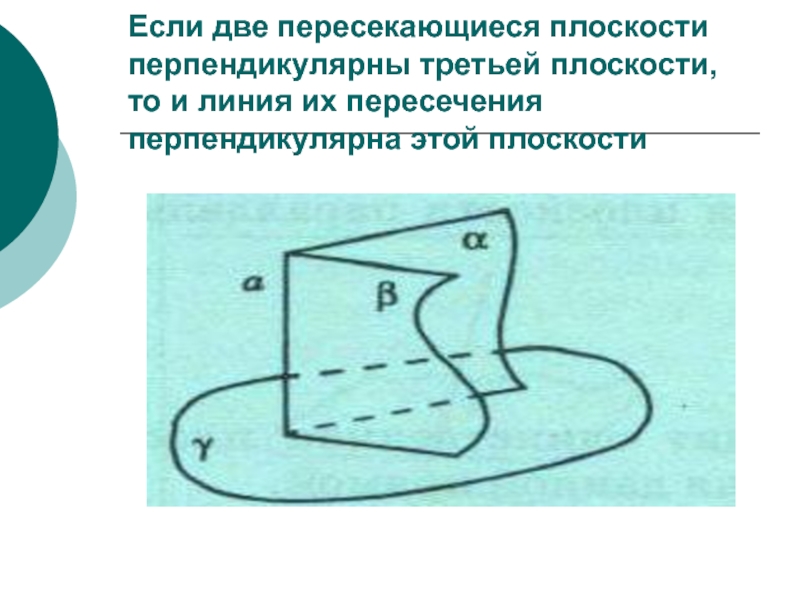
Слайд 73Если две пересекающиеся плоскости перпендикулярны третьей плоскости,
то и линия
их пересечения перпендикулярна этой плоскости
Слайд 74
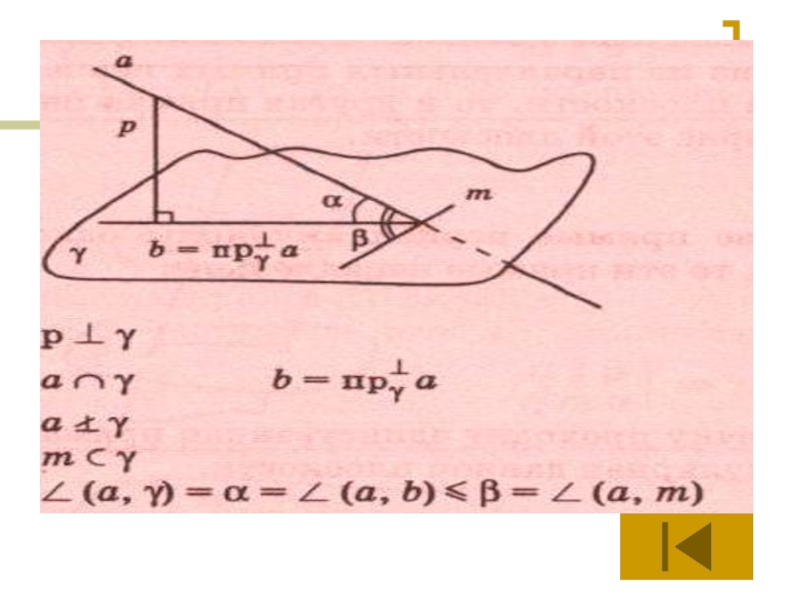
Угол, образованный наклонной и плоскостью, не больше угла между этой
наклонной и любой прямой плоскости.
Углом между наклонной и плоскостью называется
угол между наклонной и ее ортогональной проекцией на эту плоскость.
Слайд 77Карточка 1
Точки A, B, C, D не лежат в одной
плоскости. Могут ли прямые AB и CD пересекаться?
Через точки K,
L и середину N отрезка KL проведены параллельные прямые, пересекающие некоторую плоскость α в точках K1, L1, N1 соответственно. Найдите длину отрезка NN1, если KK1 = 15 м, LL1 = 5 м, причем отрезок KL не пересекает плоскость α.
Слайд 78Карточка 2
Точки K, L, M, T не лежат в одной
плоскости. Могут ли прямые KL и MT пересекаться?
Через точки A,
B и середину N отрезка AB проведены параллельные прямые, пересекающие некоторую плоскость α в точках A1, B1, N1 соответственно. Найдите длину отрезка NN1, если AA1 = 10 м, BB1 = 8 м, причем отрезок AB не пересекает плоскость α.
Слайд 79Карточка 3
Прямые b и c пересекаются. Прямая f является скрещивающейся
с прямой b. Могут ли прямые с и f быть
параллельными? Ответ обоснуйте.
Плоскость β проходит через середины боковых сторон AB и CD трапеции ABCD – точки S и P. Докажите, что AD || β. Найдите BC, если AD=6 м, SP =9 м.
Слайд 80Карточка 4
Прямые а и b пересекаются. Прямая k является скрещивающейся
с прямой а. Могут ли прямые b и k быть
параллельными? Ответ обоснуйте.
Плоскость β проходит через середины боковых сторон AB и CD трапеции ABCD – точки S и P. Докажите, что AD || β. Найдите BC, если AD=12 см, SP =10см.
Слайд 81Карточка 1
Через точки А и В проведены прямые, перпендикулярные плоскости
β, пересекающие её в точках С и D соответственно. Найдите
расстояние между точками А и В, если АС = 8 см, ВD= 5 см, СD= 4 см и отрезок АВ не пересекает плоскость β.
Слайд 82Карточка 2
Через точки М и К проведены прямые, перпендикулярные плоскости
α, пересекающие её в точках Т и L соответственно. Найдите
расстояние между точками М и К, если МТ= 12 см, КL = 8 см, ТL = 3 см и отрезок МК не пересекает плоскость α.
Слайд 83Карточка 3
Телефонная проволока длиной 10 м. протянута от телефонного столба,
где она прикреплена на высоте 12 м. от поверхности земли,
к дому, где её прикрепили на высоте 18 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
Слайд 84Карточка 4
Телефонная проволока длиной 10 м. протянута от телефонного столба,
где она прикреплена на высоте 14 м. от поверхности земли,
к дому, где её прикрепили на высоте 22 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
Слайд 85Карточка 1
Точка отстоит от плоскости на 12 см; из неё
проведена к плоскости наклонная, равная 13 см. Чему равна проекция
этой плоскости?
CDEK – квадрат, диагональ которого равна 8 см. BD перпендикулярно плоскости CDE. Найдите расстояние от точки B до плоскости CDE, BK=10 см.
Слайд 86Карточка 2
Точка отстоит от плоскости на 8 см; из неё
проведена к плоскости наклонная, равная 10 см. Чему равна проекция
этой плоскости?
CDEK – квадрат, диагональ которого равна 12 см. BD перпендикулярно плоскости CDE. Найдите расстояние от точки B до плоскости CDE, BK=13 см.
Слайд 87Параллельность прямых и плоскостей
№ 1
Через концы отрезка СD и его
середину К проведены параллельные прямые, пересекающие некоторую плоскость в точках
С1, D1 и К1.Найдите длину отрезка КК1, если отрезок СD не пересекает плоскость и СС1=8 см, DD1=10 см.
СС1=10 см, DD1=12 см.(второй вариант)
Слайд 88№ 2
Плоскость β проходит через основание КL трапеции КМNL. А
и В – середины боковых сторон трапеции. Докажите, что АВ||β.
Найдите КL, если МN=5 см, АВ = 7 см.
МN=7 см, АВ = 9 см. (второй вариант)
Слайд 89№ 3
Даны параллельные плоскости β и γ. Через точки С
и D плоскости проведены параллельные прямые, пересекающие плоскость γ в
точках С1 и D1. Найдите С1D1, если СD=9 см.
СD=10 см. (второй вариант)
Слайд 90№ 4
Докажите, что все прямые, пересекающие две данные параллельные прямые,
лежат в одной плоскости.
Слайд 91№ 5
Параллельные прямые а и b пересекают одну из двух
параллельных плоскостей в точках А1 и В1, а другую в
точках А2 и В2 соответственно. Найдите <А2А1В1, если <А1А2В2 = 140°
<А1А2В2 = 150°(второй вариант)
Слайд 92Перпендикулярность прямых и плоскостей. № 1
1. Через точки А и
В проведены прямые, перпендикулярные плоскости α, пересекающие её в точках
Си Д соответственно. Найдите расстояние между точками А и В, если отрезок АВ не пересекает плоскость α и АС = 10 см, ВД = 4 см, СД = 8 см.
(Второй вариант: АС = 10 см, ВД = 2 см, СД = 6 см.)
Слайд 93№ 2
Точка А отстоит от плоскости на расстояние 4
м. Найти длину наклонной, проведенной из этой точки под углом
30° к плоскости.
(Второй вариант: Точка А отстоит от плоскости на расстояние 6 м.)
Слайд 94№ 3
Дан прямоугольник АВСД. Через точку О пересечения его диагоналей
проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от т.
К до вершин прямоугольника, если ОК =24 см, АВ =12 см, АД =16 см.
Слайд 95Вопросы
1) Как называется раздел геометрии, изучающий фигуры в пространстве?
2) Как
называется раздел геометрии, изучающий фигуры на плоскости?
3) Назовите основные фигуры
в пространстве?
4) Могут ли прямая и плоскость иметь две общие точки?
5) Сколько плоскостей можно провести через три точки?
6) Сколько плоскостей можно провести через прямую и не лежащую на ней точку?
7) Сколько может быть общих точек у прямой и плоскости?
8) Могут ли прямая и плоскость иметь одну общую точку?
Слайд 96Задания
Верно ли, что две прямые называются перпендикулярными в пространстве, если
они пересекаются под углом 180º?
Верно ли, что две прямые,
перпендикулярные одной и той же плоскости, параллельны?
Верно ли, что через данную точку плоскости можно провести одну и только одну перпендикулярную ей прямую?
Верно ли, что перпендикуляр, проведенный из данной точки к плоскости, больше любой наклонной, проведенной из той же точки к плоскости?
Верно ли, что если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости?
Верно ли утверждение: Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?
Слайд 97Тестовые задания
Аксиомы стереометрии и следствия из них.
Взаимное расположение прямых в пространстве. Угол
между прямыми.
Параллельность прямых и плоскостей.
Перпендикулярность прямой и плоскости.
Перпендикуляр и наклонные.
Слайд 98Тема «Аксиомы стереометрии и следствия из них».
Вариант 1.
1. Какое из
следующих утверждений верно?
а) любые четыре точки лежат в одной плоскости;
б) любые три точки не лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость; д) через любые три точки проходит плоскость, и притом только одна.
2. Сколько общих точек могут иметь две различные плоскости?
а) 2; б) 3; в) несколько; г) бесконечно много; д) бесконечно много или ни одной.
3. Точки А, В, С лежат на одной прямой, точка D не лежит на ней. Через
каждые три точки проведена одна плоскость. Сколько различных
плоскостей при этом получилось?
а) 2; б) 3; в) 1; г) 4; д) бесконечно много.
4. Если три точки не лежат на одной прямой, то положение плоскости в
пространстве они:
а) не определяют в любом случае; б) определяют, но при дополнительных условиях;
в) определяют в любом случае; г) ничего сказать нельзя; д) другой ответ.
5. Выберите верное утверждение.
а) Если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна; в) через две пересекающиеся прямые плоскость провести нельзя; г) любые две плоскости не имеют общих точек; д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой.

Слайд 99Тема «Аксиомы стереометрии и следствия из них».
Вариант 2.
1.Что можно сказать
о взаимном расположении двух плоскостей, которые имеют три общие точки,
не лежащие на одной прямой?
а) Пересекаются; б) ничего сказать нельзя; в) не пересекаются; г) совпадают; д) имеют три общие точки.
2. Какое из следующих утверждений верно?
а) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны; в) любые две плоскости имеют только одну общую точку; г) через две точки проходит плоскость и притом только одна; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
3. Могут ли две различные плоскости иметь только две общие точки?
а) Никогда; б) могу, но при дополнительных условиях; в) всегда имеют; г) нельзя ответить на вопрос; д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось?
а) 1; б) 2; в) 3; г) 4; д) бесконечно много.
5. Выберите верное утверждение.
а) Через любые три точки проходит плоскость, и притом только одна; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости; в) если две плоскости имеют общую точку, то они не пересекаются; г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна; д) через две пересекающиеся прямые плоскость провести нельзя.

Слайд 100Тема «Взаимное расположение прямых в пространстве. Угол между прямыми».
Вариант 1.
1. Выясните взаимное расположение прямых АС и КС.
а) Параллельны;
б) определить нельзя; в) скрещиваются; г) пересекаются; д) совпадают в
любом случае.
2. Точка М не лежит в плоскости треугольника ABC, K – середина MB. Каково взаимное расположение прямых MA и CK?
а) Определить нельзя; б) скрещиваются; в) параллельны; г) совпадают; д) пересекаются.
3. Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b?
а) Взаимное расположение точно определить нельзя; б) скрещиваются или параллельны; в) параллельны или пересекаются; г) совпадают; д) пересекаются или скрещиваются.
4. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда:
а) прямые а и с пересекаются; б) прямая с лежит в плоскости α; в) прямые а и с скрещиваются; г) прямая b лежит в плоскости α; д) прямые а и спараллельны.
5. В треугольнике ABC угол А на 30˚ больше суммы углов В и С. Найдите угол между прямыми АС и ВС.
а) 105˚; б) 75˚; в) 37,5˚; г) 30˚; д) определить нельзя.
Слайд 101Тема «Взаимное расположение прямых в пространстве. Угол между прямыми».
Вариант 2.
1. Выясните взаимное расположение прямых MN и NP.
а) Параллельны;
б) скрещиваются; в) определить нельзя; г) пересекаются; д) совпадают в
любом случае.
2. Точка М не лежит в плоскости четырехугольника ABCD, K – середина МА. Каково взаимное расположение прямых МВ и DK?
а) Определить нельзя; б) скрещиваются; в) параллельны; г) пересекаются; д) совпадают.
3. Прямые а и с скрещиваются с прямой b. Что можно сказать о прямых а и c?
а) параллельны или пересекаются; б) скрещиваются или параллельны; в) взаимное расположение определить точно нельзя; г) пересекаются или скрещиваются; д) совпадают.
4. Прямая с, параллельная прямой а, пересекает плоскость β. Прямая b параллельна прямой а, тогда:
а) прямые b и с пересекаются; б) прямая b лежит в плоскости β; в) прямые b и с скрещиваются; г) прямые b и с параллельны; д) прямая а лежит в плоскости β.
5. В треугольнике ABC угол С на 40˚ больше суммы углов В и А. Найдите угол между прямыми АС и ВС.
а) 110˚; б) 70˚; в) 55˚; г) 125˚; д) определить нельзя.
Слайд 102Тема «Параллельность прямых и плоскостей».
Вариант 1.
1. Каким может быть взаимное
расположение прямых а и b, если прямая а лежит в плоскости α, а прямая b параллельна этой плоскости?
а) Параллельны
или пересекаются; б) скрещиваются или пересекаются; в) параллельны или скрещиваются; г) определить нельзя; д) совпадают.
2. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α; б) прямая а не пересекает ни одну прямую, лежащую в плоскости α; в) прямая аскрещивается со всеми прямыми плоскости α; г) прямая а имеет общую точку с плоскостью α; д) прямая а лежит в плоскости α.
3. Даны треугольник АВС и плоскость α, причем АВ║α, АС║α, тогда прямая ВС и плоскость α:
а) параллельны; б) пересекаются; в) прямая лежит в плоскости; г) определить нельзя; д) другой ответ.
4. Через концы отрезка АВ , не пересекающего плоскость α и точку С – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость α в точках А1, В1 ,С1 соответственно. Найдите длину отрезка СС1, если АА1 = 12, ВВ1 = 6.
а) 6; б) 9; в) 6√2; г) 9√2; д) другой ответ.
5. Прямая а параллельна прямой b и плоскости α. Выберите верное утверждение.
а) Прямая b параллельна плоскости α; б) прямая b лежит в плоскости α; в) прямая b пересекает плоскость α; г) прямая b лежит в плоскости α или параллельна ей; д) прямая b скрещивается с плоскостью α.

Слайд 103Тема «Параллельность прямых и плоскостей».
Вариант 2.
1. Каким может быть взаимное
расположение двух прямых, если обе они параллельны одной плоскости?
а) Только
параллельны; б) определить нельзя; в) все случаи взаимного расположения; г) только скрещиваются; д) только пересекаются.
2. Прямая b параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая b параллельна любой прямой, лежащей в плоскости α; б) прямая b параллельна некоторой прямой, лежащей в плоскости α; в) прямая bпересекается со всеми прямыми плоскости α; г) прямая b пересекается с некоторой прямой плоскости α; д) любая плоскость, проходящая через прямую b, пересекает плоскость α.
3. Даны трапеция ABCD и плоскость α. Диагонали трапеции AC и BD параллельны плоскости α. Тогда прямая BA и плоскость α:
а) Параллельны; б) пересекаются; в) определить нельзя; г) прямая лежит в плоскости; д) другой ответ.
4. В треугольнике АВС точки F и E принадлежат сторонам СВ и АВ соответственно, причём ВЕ : ЕА = 2 : 3. Через эти точки провели плоскость, параллельную АС. Найдите отношение BF : FC.
а) 3 : 2; б) 2 : 3; в) 3 : 5; г) 2 : 5; д) Определить нельзя.
5. Прямая а параллельна плоскости α, точка М принадлежит этой плоскости. Выберете верное утверждение.
а) Точка М принадлежит прямой а; б) любая прямая, проходящая через точку М, будет параллельна прямой а; в) в плоскости α существует прямая, проходящая через точку М и параллельная прямой а; г) существует прямая, не лежащая в плоскости α, которая проходит через точку М и параллельная прямой а; д) в плоскости α существуют две прямые, проходящие через точку М и параллельные прямой а.

Слайд 104Тема «Перпендикулярность прямой и плоскости».
Вариант 1.
1. Какое из следующих утверждений
неверно?
а) Если одна из двух параллельных прямых перпендикулярна третьей прямой,
то и другая прямая перпендикулярна к этой прямой;
б) прямая называется параллельной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости;
в) две прямые, перпендикулярные к плоскости, параллельны;
г) если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости;
д) через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
2. Две скрещивающиеся прямые взаимно перпендикулярны. Чему равен угол между ними?
а) 900; б) 00; в) 1800; г) 450; д) определить нельзя.
3. Через вершину квадрата ABCD проведена прямая AM, перпендикулярная его плоскости. Какое из следующих утверждений неверно?
а) MA BD; б) MD CD; в) MB BC; г) MC BC; д) MA AC .
4. Дан правильный треугольник ABC со стороной, равной 3. Точка O – центр треугольника, OM – перпендикуляр к его плоскости, OM = 1. Найдите расстояния от точки Mдо вершин треугольника. а) ; б) определить нельзя; в) 3; г) 1; д) 2.
5. Прямая m перпендикулярна к прямым a и b, лежащим в плоскости α, но m не перпендикулярна к плоскости α. Выясните взаимное расположение прямых a и b.
а) Параллельны; б) пересекаются; в) скрещиваются; г) совпадают; д) определить нельзя.

Слайд 105Тема «Перпендикулярность прямой и плоскости».
Вариант 2.
1. Если угол между двумя прямыми
равен 900, то эти прямые:
а) пересекаются; б) параллельны; в) скрещиваются; г) перпендикулярны;
д) совпадают.
2. Какое из следующих утверждений неверно?
а) Если прямая перпендикулярна к двум прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости;
б) если прямая перпендикулярна к плоскости, то она ее пересекает;
в) если две плоскости перпендикулярны к прямой, то они параллельны;
г) если две прямые перпендикулярны к плоскости ,то они параллельны;
д) если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
3. Если одна из двух скрещивающихся прямых перпендикулярна к плоскости, то будет ли перпендикулярна к этой плоскости вторая прямая?
а) Да; б) да, но при определенных условиях; в) определить нельзя; г) нет; д) другой ответ.
4. ABCD – квадрат со стороной, равной , O – точка пересечения его диагоналей, OE – перпендикуляр к плоскости ABC, OE = . Найдите расстояние от точки E до вершин квадрата. а) Определить нельзя; б) ; в) ; г) 1; д) 2.
5. Прямая а перпендикулярна к прямым с и b, лежащим в плоскости α, прямая а перпендикулярна к плоскости α. Выясните взаимное расположение прямых с и b.
а) Параллельны; б) пересекаются; в) параллельны или пересекаются; г) совпадают; д) определить нельзя.

Слайд 106Тема «Перпендикуляр и наклонные».
Вариант 1.
1. Из точки М к плоскости α проведены две наклонные, длины
которых 18см и 2 см. Их проекции на эту плоскость относятся как 3 : 4. Найдите расстояние от
точки М до плоскости α.
а) 6 см; б) 30см; в) 6см; г) 3 см; д) 2 см.
2. Какое из следующих утверждений неверно?
а) Перпендикуляр и наклонная, выходящие из одной точки, имеют разную длину;
б) расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из данной точки к данной плоскости; в) равные наклонные, проведенные к плоскости из одной точки, имеют разные проекции; г) проекцией точки на плоскость является точка; д) углом между прямой и плоскостью, пересекающей эту прямую и неперпендикулярной к ней, называется угол между прямой и ее проекцией на эту плоскость.
3. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4см. Найдите расстояние от точки M до плоскости ABC, еслиAB = 6см.
а) 4см; б) 16 - 2 см; в) 8см; г) 6см; д) 2см.
4. Через точку А, удаленную от плоскости α на 4см, проходит прямая, пересекающая плоскость α в точке В. Найдите угол между прямой АВ и плоскостью α, если длина отрезка АВ равна 6см.
а) arccos2/3; б) arcsin2/3; в) arcsin3/2; г) arctg2/3; д) arcctg2/3.
5. Из точки к плоскости проведены две равные наклонные. Величина угла между этими наклонными равна 600. Величина угла между их проекциями равна 900. Найдите угол между каждой наклонной и ее проекцией.
а) 900; б) 600; в) 300; г) 450; д) определить нельзя.

Слайд 107Тема «Перпендикуляр и наклонные».
Вариант 2.
1. Из точки М к плоскости α проведены две наклонные, длины
которых 18см и 2 см. Их проекции на эту плоскость относятся как 4 : 3. Найдите расстояние от
точки М до плоскости α.
а) 34см; б) 2 см; в) 2см; г) 2 см; д) 10 см.
2. Какое из следующих утверждений неверно?
а) Перпендикуляр и наклонная, выходящие из одной точки, имеют равные длины;
б) проекцией прямой на плоскость является точка или прямая; в) наклонные разной длины, проведенные к плоскости из одной точки, имеют проекции разных длин; г) прямая, проведенная к плоскости через основание наклонной перпендикулярно к ней, перпендикулярна к ее проекции; д) расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
3. Расстояние от точки К до каждой из вершин квадрата ABCD равно 4см. Найдите расстояние от точки K до плоскости ABC, если AB = 2см.
а) 4 - см; б) 14см; в) 2см; г) см; д) 2 см.
4. Через точку А, удаленную от плоскости α на 3см, проходит прямая, пересекающая плоскость α в точке В. Угол между прямой АВ и плоскостью αравен arcsin0,6. Найдите длину отрезка АВ.
а)4см; б)3см; в)6см; г)50см; д)5см.
5. Из точки к плоскости проведены две равные наклонные. Величина угла между этими наклонными равна 600. Найдите величину угла между их проекциями, если угол между каждой наклонной и ее проекцией равен 450.
а) 300; б) 450; в) 600; г) 900; д) определить нельзя.