Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Стереометрия"
Содержание
- 1. Презентация по теме "Стереометрия"
- 2. Содержание:МногогранникиПрямоугольный параллелепипед;Прямая призма;Наклонная призма;Пирамида;Усеченная пирамида.Тела, полученные при вращенииЦилиндр;Конус;Усеченный конус;Сфера;Шар.
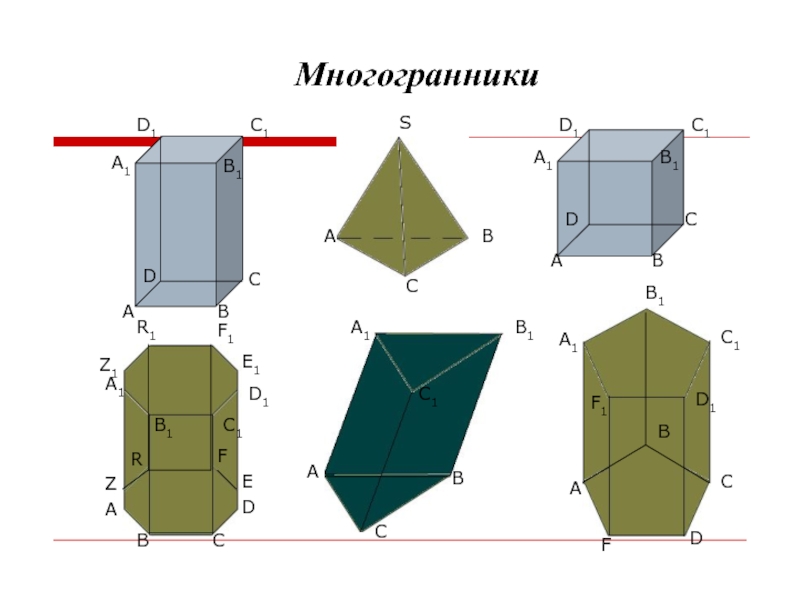
- 3. МногогранникиABCDA1B1C1D1ABCSABCDA1B1C1D1ABCDEFRA1B1C1D1E1F1R1Z1ZABCDFA1B1C1D1F1
- 4. Прямоугольный параллелепипед.Прямоугольный параллелепипед – это прямой параллелепипед,
- 5. Прямая призма.Призма – это многогранник, у которого
- 6. Наклонная призма.Наклонной призмой называется призма, не являющаяся
- 7. Пирамида.Пирамида – многогранник, у которого одна грань
- 8. Усеченная пирамида.Усеченная пирамида – пирамида, через точку
- 9. Цилиндр, конус, шар.АВОА1В1О1АВОС
- 10. Цилиндр.Цилиндр – тело, ограниченное цилиндрической поверхностью и
- 11. Конус.Конус – геометрическое тело, ограниченное конической поверхностью
- 12. Усеченный конус.Усеченный конус – часть прямого кругового
- 13. Сфера.Сфера – поверхность, состоящая из всех точек
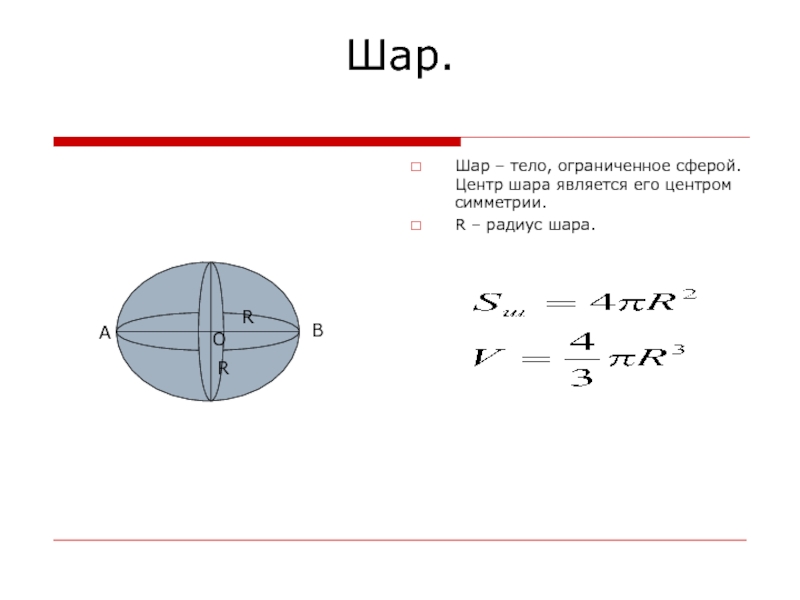
- 14. Шар.Шар – тело, ограниченное сферой. Центр шара является его центром симметрии. R – радиус шара.RRАВО
- 15. Скачать презентанцию
Содержание:МногогранникиПрямоугольный параллелепипед;Прямая призма;Наклонная призма;Пирамида;Усеченная пирамида.Тела, полученные при вращенииЦилиндр;Конус;Усеченный конус;Сфера;Шар.
Слайды и текст этой презентации
Слайд 1Стереометрия.
Мы с геометрией на «ты»,
Умеем складывать плоты,
Умеем площадь измерять
И симметричность
проверять.
Слайд 2Содержание:
Многогранники
Прямоугольный параллелепипед;
Прямая призма;
Наклонная призма;
Пирамида;
Усеченная пирамида.
Тела, полученные при вращении
Цилиндр;
Конус;
Усеченный конус;
Сфера;
Шар.
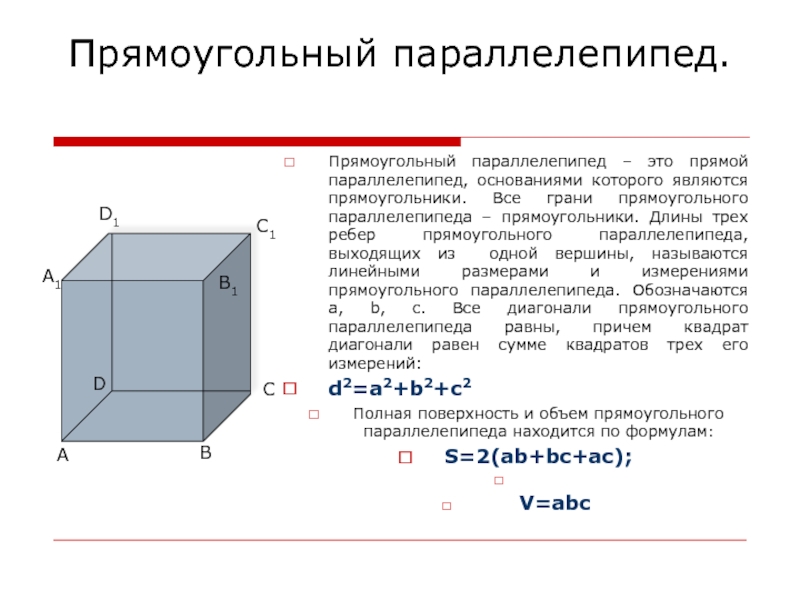
Слайд 4Прямоугольный параллелепипед.
Прямоугольный параллелепипед – это прямой параллелепипед, основаниями которого являются
прямоугольники. Все грани прямоугольного параллелепипеда – прямоугольники. Длины трех ребер
прямоугольного параллелепипеда, выходящих из одной вершины, называются линейными размерами и измерениями прямоугольного параллелепипеда. Обозначаются a, b, c. Все диагонали прямоугольного параллелепипеда равны, причем квадрат диагонали равен сумме квадратов трех его измерений:d2=a2+b2+c2
Полная поверхность и объем прямоугольного параллелепипеда находится по формулам:
S=2(ab+bc+ac);
V=abc
Слайд 5Прямая призма.
Призма – это многогранник, у которого две грани –
равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней
– параллелограммы. Два n-угольника -основания призмы, параллелограммы – боковые гранями. Стороны боковых граней и оснований -ребра призмы, концы ребер - вершины призмы. Боковыми ребрами называются ребра, не принадлежащие основаниям. Объединение боковых граней - боковая поверхность призмы, а граней – полная поверхность призмы. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания - высотой призмы(h). Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.Sбок. пов.=Ph;
Sпол.пов.= Sбок. пов+2 Sосн.;
V= Sоснh,
P-периметр основания
А
В
С
А1
С1
h
В1
Слайд 6Наклонная призма.
Наклонной призмой называется призма, не являющаяся прямой
Sбок. пов.=Ph;
Sпол.пов.=
Sбок. пов+2 Sосн.;
V= Sоснh,
P-периметр основания;
h – высота наклонной призмы
(ОВ)О
h
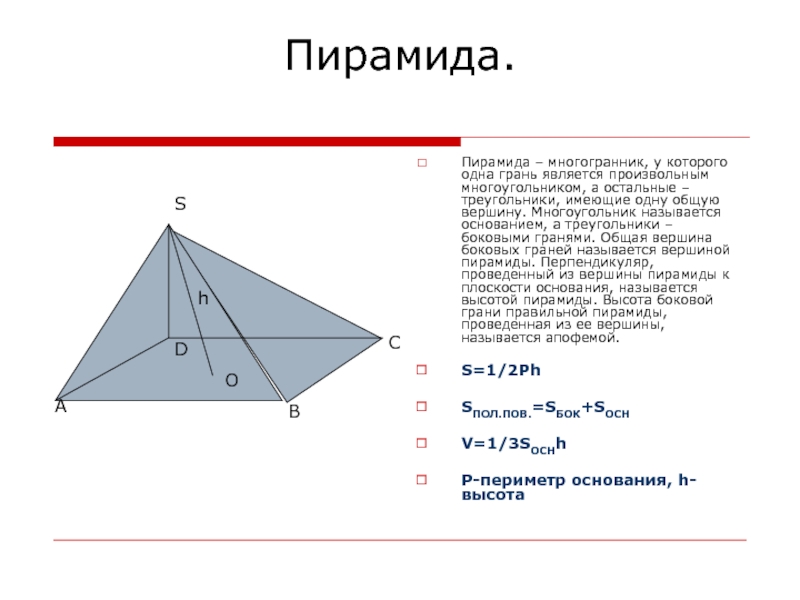
Слайд 7Пирамида.
Пирамида – многогранник, у которого одна грань является произвольным многоугольником,
а остальные – треугольники, имеющие одну общую вершину. Многоугольник называется
основанием, а треугольники – боковыми гранями. Общая вершина боковых граней называется вершиной пирамиды. Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.S=1/2Ph
SПОЛ.ПОВ.=SБОК+SОСН
V=1/3SОСНh
P-периметр основания, h-высота
h
Слайд 8Усеченная пирамида.
Усеченная пирамида – пирамида, через точку бокового ребра проводится
параллельная плоскость основанию пирамиды. Основаниями усеченной пирамиды служат подобные многоугольники.
Перпендикуляр. Проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды(h). Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и боковых граней.Слайд 10Цилиндр.
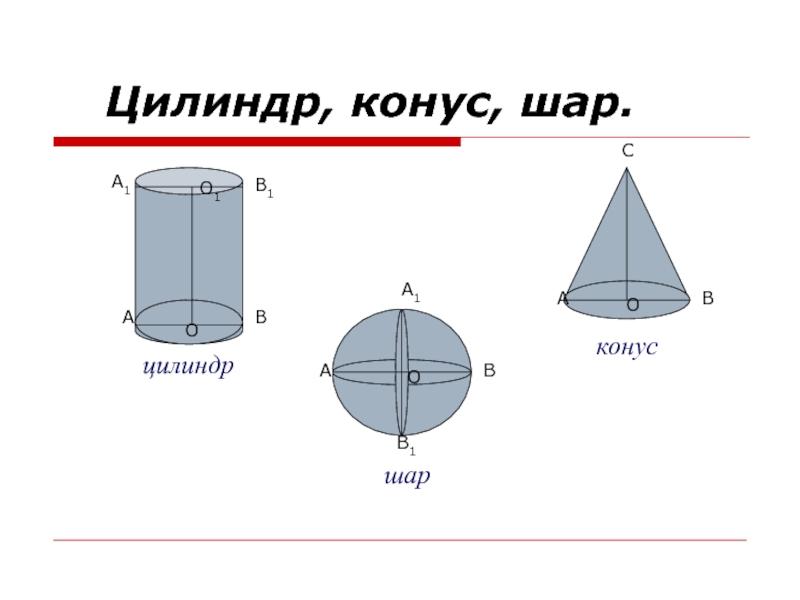
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями.
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями
цилиндра. Образующие цилиндрической поверхности называются образующими цилиндра, прямая ОО1-осью цилиндра. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра. За площадь боковой поверхности цилиндра принимается площадь ее развертки.A
B
O
O1
A1
B1
h
r
h
Слайд 11Конус.
Конус – геометрическое тело, ограниченное конической поверхностью с замкнутой направляющей
и пересекающей ее плоскость, не проходящей через вершину конической поверхности.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость основания.SO – высота h
SA – образующая
AO –радиус основания r.
A
O
B
S
h
r
Слайд 12Усеченный конус.
Усеченный конус – часть прямого кругового конуса, ограниченная его
основанием и сечением, параллельным плоскостям основания.
OO1 – высота h
AA1
– образующая AO = r – радиус нижнего основания
A1O = r1 радиус верхнего основания
A
B
A1
B1
O1
O
h
r
r1
Слайд 13Сфера.
Сфера – поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии от данной точки. Данная точка называется центром сферы(О),
а данное расстояние – радиусом сферы(r). Любой отрезок соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Если сфера заданна в прямоугольной декартовой системе координат, то ее уравнение имеет вид:(x-x0)2 + (y-y0)2 + (z-z0)2 =R2, где О(x0,y0,z0) – центр сферы, R – радиус сферы.
ОВ- радиус сферы
О – центр сферы
АВ – диаметр сферы