Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация проекта "Математика и искусство"
Содержание
- 1. Презентация проекта "Математика и искусство"
- 2. ВведениеЦель работы: Выполнение презентации «Связь математики
- 3. ВведениеНаука и искусство – два основных начала
- 4. Золотое сечениеЗолотым сечением (делением) и даже “божественной
- 5. Ряд ФибоначчиС историей золотого сечения косвенным образом
- 6. Золотое сечение
- 7. Золотое сечениеПортрет Моны Лизы Леонардо да Винчи.
- 8. Золотое сечениеФасад Парфенона в Афинах вписывается в
- 9. Золотое сечениеЗолотое сечение мы можем увидеть и
- 10. Золотое сечениеЗолотая пропорция применялась многими античными скульпторами.
- 11. Математика и живопись
- 12. Математика и живописьИсторически, математика играла важную роль
- 13. «Ортогональная» живопись Древнего ЕгиптаОртогональная перспектива свойственна древнеегипетскому
- 14. «Параллельная» живопись средневекового Китая и ЯпонииВ искусстве
- 15. «Параллельная» живопись средневекового Китая и Японии
- 16. Линейная перспектива эпохи Возрождения.
- 17. Линейная перспектива эпохи ВозрожденияВ картине Леонардо да
- 18. Линейная перспектива эпохи Возрождения
- 19. Обратная перспектива живописи Древней РусиОсобый вид перспективы
- 20. Обратная перспектива живописи Древней Руси
- 21. Математика и архитектураСтоит лишь вспомнить классические творения
- 22. Математика и архитектура Успенский собор. Владимир.Архитектура —
- 23. Математика и архитектураСтруи бьющих фонтанов привлекают правильностью
- 24. Математика и музыкаО влиянии музыки на человека
- 25. Математика и музыка Великий немецкий композитор XVII
- 26. Математика и музыкаВосемь звуков- до, ре, ми,
- 27. Математика и поэзияМногое в структуре произведений поэзии
- 28. Математика и поэзияИсследователи вычислили, что числа Фибоначчи
- 29. Математика и поэзия Символику чисел использует в своей
- 30. ЗаключениеНастоящее искусство имеет свою теорию. Иногда эту
- 31. Информационно-познавательный проект «Математика и искусство»Выполнила Байкалова
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Информационно-познавательный проект
«Математика и искусство»
Автор проекта:
Байкалова Дарья, ученица 7А
класса МБОУ СОШ №126 имени Героя России Д. Новоселова
Любовь НиколаевнаСлайд 2Введение
Цель работы:
Выполнение презентации «Связь математики и различных
видов искусства»
Задачи:
1) Изучить научно-популярную литературу и интернет-источники
2) На основе информационных
источников выбрать наиболее интересные примеры связи математики и искусства3) Подготовить презентацию работы
Слайд 3Введение
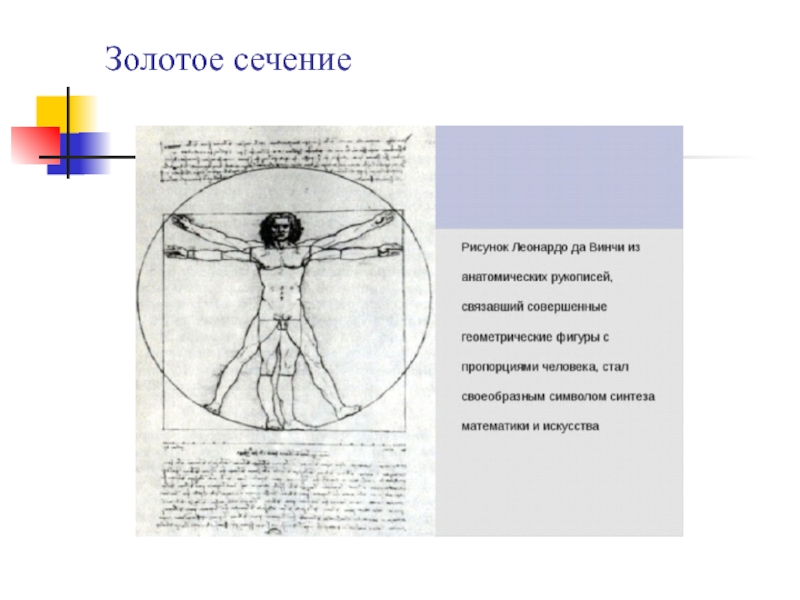
Наука и искусство – два основных начала в человеческой культуре,
две дополняющие друг друга формы высшей творческой деятельности человека.
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты. Искусство –творческое отражение, воспроизведение действительности в художественных образах.
Слайд 4Золотое сечение
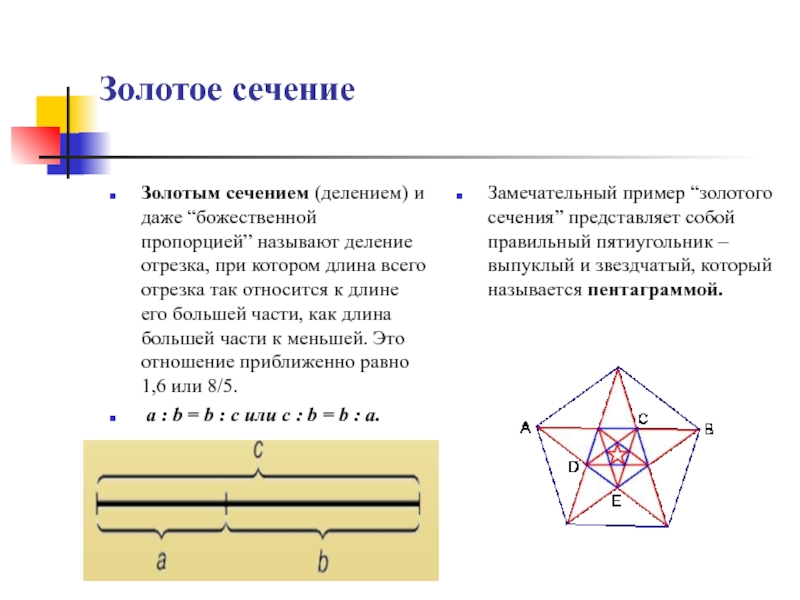
Золотым сечением (делением) и даже “божественной пропорцией” называют деление
отрезка, при котором длина всего отрезка так относится к длине
его большей части, как длина большей части к меньшей. Это отношение приближенно равно 1,6 или 8/5.a : b = b : c или с : b = b : а.
Замечательный пример “золотого сечения” представляет собой правильный пятиугольник – выпуклый и звездчатый, который называется пентаграммой.
Слайд 5Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского
математика монаха Леонардо из Пизы, более известного под именем Фибоначчи.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.Слайд 7Золотое сечение
Портрет Моны Лизы Леонардо да Винчи. Композиция рисунка построена
на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина
(«Сосновая роща») так же просматриваются мотивы золотого сечения.Слайд 8Золотое сечение
Фасад Парфенона в Афинах вписывается в прямоугольник, стороны которого
образуют золотое сечение. Длина прямоугольника больше его ширины примерно в
1,6 раза.Золотое сечение можно встретить в бытовых предметах и шрифтах.
Слайд 9Золотое сечение
Золотое сечение мы можем увидеть и в здании собора
Парижской Богоматери, и в пирамиде Хеопса, и в храме Василия
Блаженного на Красной площади.Слайд 10Золотое сечение
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция
статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в
золотом сечении .Слайд 12Математика и живопись
Исторически, математика играла важную роль в изобразительном искусстве,
в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены
на плоском холсте или листе бумаги.Слайд 13«Ортогональная» живопись
Древнего Египта
Ортогональная перспектива свойственна древнеегипетскому искусству .Человеческая фигура рисовалась
в несколько странном ракурсе: голова и ноги давались в профиль.
А грудь и плечи рисовались в фас, повернутыми к зрителю.Слайд 14«Параллельная» живопись
средневекового Китая и Японии
В искусстве Китая применялась геометрия живописи
– аксонометрия. Аксонометрия - есть центральная проекция с бесконечно удалённым
центром проектирования. Таким образом, именно в этой геометрической системе точка зрения художника отодвигалась в бесконечность, художник растворялся в безграничных пространствах природы и бесстрастно взирал на её мудрое спокойствие.Слайд 16Линейная перспектива эпохи Возрождения.
Перспектива - лучший
приём передачи видимого. Для Возрождения наиболее характерна линейная перспектива. Линия
горизонта и главная точка картины стали важнейшими инструментами художника. Главная точка картины заключала в себе смысл картины, становилась смысловым центром картины. Открытие способа изображения трехмерного пространства на плоскости при помощи линейной (прямой) перспективы знаменует наступление новой эры в европейском искусстве - реализма. Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия – в искусство
Слайд 17Линейная перспектива эпохи Возрождения
В картине Леонардо да Винчи "Тайная вечеря"
таким центром является правый глаз Христа.
Вся картина построена на
линиях исходящих из этого центра. Картина имеет строгую вертикальную симметрию.«Тайная вечеря» - это наука и искусство, которые для Леонардо да Винчи были слиты в живописи воедино.
Слайд 19Обратная перспектива живописи Древней Руси
Особый вид перспективы использовали древнерусские живописцы
в иконописи, фресках, миниатюре. Они рисовали параллельные линии, уходящие вдаль
расходящимися, а не сходящимися, то есть в обратной перспективе.Слайд 20 Обратная перспектива живописи Древней Руси Например, "Троица" Андрея Рублёва
- шедевр древнерусской живописи.
Слайд 21Математика и архитектура
Стоит лишь вспомнить классические творения архитектуры, начиная с
древнейших пирамид, как сразу становится очевидным, что геометрия в некотором
смысле относится к искусству.Принцип "симметрии" широко используется в искусстве. Бордюры в архитектурных и скульптурных произведениях, орнаменты в прикладном искусстве, здания - все это примеры использования симметрии.
Большой Сфинкс
Слайд 22Математика и архитектура
Успенский собор. Владимир.
Архитектура — удивительная область человеческой
деятельности. В ней тесно переплетены и строго уравновешены наука, техника
и искусство. Люди с доисторических времён строят удивительно красивые сооружения, в которых используют знания из различных областей науки.Рим. Колизей
Слайд 23Математика и архитектура
Струи бьющих фонтанов привлекают правильностью и красотою своих
линий, хотя не каждый знает, что это параболы, и тем
более не в состоянии написать их уравнения.Лондон. Тауэрский мост
Слайд 24Математика и музыка
О влиянии музыки на человека с древности было
хорошо известно многим ученым, однако на связь музыки и чисел
первым указал именно Пифагор.Благодаря трудам Пифагора математики обратили внимание на формальную сторону организации музыки – временную и частотную шкалы. С этого момента музыкальная и математическая науки пошли бок обок друг с другом. Более того, музыка начала развиваться именно благодаря математике.
Слайд 25Математика и музыка
Великий немецкий композитор XVII века Иоганн Себастьян
Бах писал церковную музыку. Позднее уже после его смерти музыканты-исследователи
выяснили, что многие мелодии композитора имеют цифровые коды - символы, а произведения точно математически просчитаны.Слайд 26Математика и музыка
Восемь звуков- до, ре, ми, фа, соль, ля,
си, до- древнейшая музыкальная гамма.
В музыке мы имеем дело
с короткими и длинными длительностями. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробейСлайд 27Математика и поэзия
Многое в структуре произведений поэзии роднит этот вид
искусства с музыкой. Чёткий ритм, закономерное чередование ударных и безударных
слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Каждый стих обладает своей музыкальной формой – своей ритмикой и мелодией. В строении стихотворений проявляются некоторые черты музыкальных композиций, закономерности музыкальной гармонии, а следовательно, и золотая пропорция, и числа Фибоначчи.Слайд 28Математика и поэзия
Исследователи вычислили, что числа Фибоначчи не только доминируют
в размерах А.С. Пушкина, они определяют во многих случаях и
внутреннюю композицию стихотворений: число стихов и число строк в них. Так, в стихотворении «Моя родословная» – 8 восьмистиший, в стихотворении «Друзьям» и «Дорожные жалобы» – 8 четверостиший. Преобладание в анализе стихотворений А.С. Пушкина чисел ряда Фибоначчи никак нельзя признать случайностью, игрой слепой вероятности. Наличие этих чисел выражает одну из фундаментальных закономерностей творческого методаСлайд 29Математика и поэзия
Символику чисел использует в своей поэме "Двенадцать" А.
Блок. Символика числа 12 известна своими необычными свойствами (напр. "чертова
дюжина").Число12 олицетворяет, в первую очередь, время: 12 часов (ноль часов) - начало новой эпохи, когда из бури и хаоса возникает новый мир. Так же 12 - это число солдат революции, и, невольно напрашивается ассоциация с двенадцатью апостолами новой, еще непонятной веры. Раскрытию авторской идеи способствует и структура поэмы. Она состоит из 12 глав, а число строк в поэме кратно 12...В заглавии романа – «Война и мир» - закодирован закон золотого сечения. Название романа построено на первых четырех членах ряда Фибоначчи 1, 2, 3, 5. Один союз, два существительных, три слова, пять букв в первом ключевом слове. Отношение ключевых слов 5:3=1,666…
Слайд 30Заключение
Настоящее искусство имеет свою теорию. Иногда эту теорию можно выразить
в терминах математики, так как она тесно связана практически со
всеми разновидностями современного искусства и искусства древних времен.Мы не осознаем, насколько наша жизнь связана с математикой. Даже такие творческие направления деятельности человека, как музыка, живопись, архитектура без математических законов не могут существовать и развиваться. И проделанная мною работу, ещё раз это доказывает.