Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по алгебре в 11 классе "Касательная к графику функции"
Содержание
- 1. Урок по алгебре в 11 классе "Касательная к графику функции"
- 2. Касательная к окружности
- 3. y=х2ху
- 4. у=1у=sinxух1
- 5. хуММ0
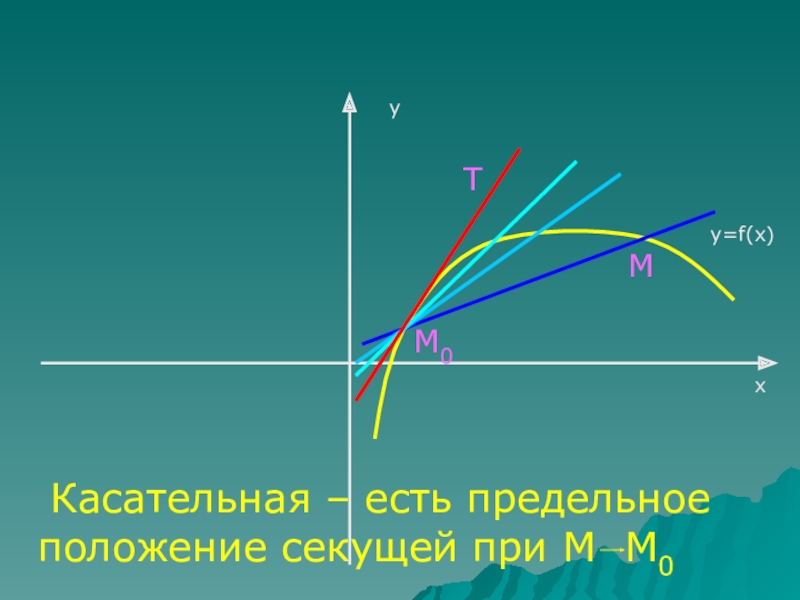
- 6. у=f(x)xy Касательная – есть предельное положение секущей при М М0ММ0Т
- 7. у=f(x)М0М1М2Т
- 8. М0МL0xyL M0, M M0
- 9. слайд 4 слайд 4
- 10. Уравнение касательнойM(x0,y0)- точка касанияЛинейное уравнение y=kx+b (1)Но
- 11. y=f(x0)+f ’(x0)(x-x0)y=f(x0)+f ’(x0)(x-x0)y=f(x0)+f ’(x0)(x-x0)y=f(x0)+f ’(x0)(x-x0)y=f(x0)+f ’(x0)(x-x0)
- 12. Скачать презентанцию
Касательная к окружности
Слайды и текст этой презентации
Слайд 1Касательная к графику функции Разработала учитель математики СОШ п. Сосновка Закирова Зиля
Махаматовна
Слайд 10Уравнение касательной
M(x0,y0)- точка касания
Линейное уравнение y=kx+b (1)
Но k=f ’(x0), то
есть
y=f ’(x0)x+b (2)
M(x0,y0)€ T, значит её координаты
удовлетворяют уравнению касательной (2)
т.е.
y0=f ’(x0)x+b, но y0=f(x0)Отсюда b=f(x0)-f ’(x0)x0 (3)
Подставим (3) в (2)
y=f ’(x0)x+f(x0)-f ’(x0)x0=
=f(x0)+f ’(x0)(x-x0)
Таким образом, уравнение касательной имеет вид
y=f(x0)+f ’(x0)(x-x0)
Слайд 11 y=f(x0)+f ’(x0)(x-x0)
y=f(x0)+f ’(x0)(x-x0)
y=f(x0)+f ’(x0)(x-x0)
y=f(x0)+f ’(x0)(x-x0)
y=f(x0)+f ’(x0)(x-x0)
