Применение теоремы Пифагора

Содержание

1. Применение теоремы Пифагора
2. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора». Иоганн Кеплер
3. Долина устных задачОстров НезнаекПолянка ЗдоровьяКрепость ФормулИсторическая тропинка
4. (580 - 500 г. до н.э.)Пифагор
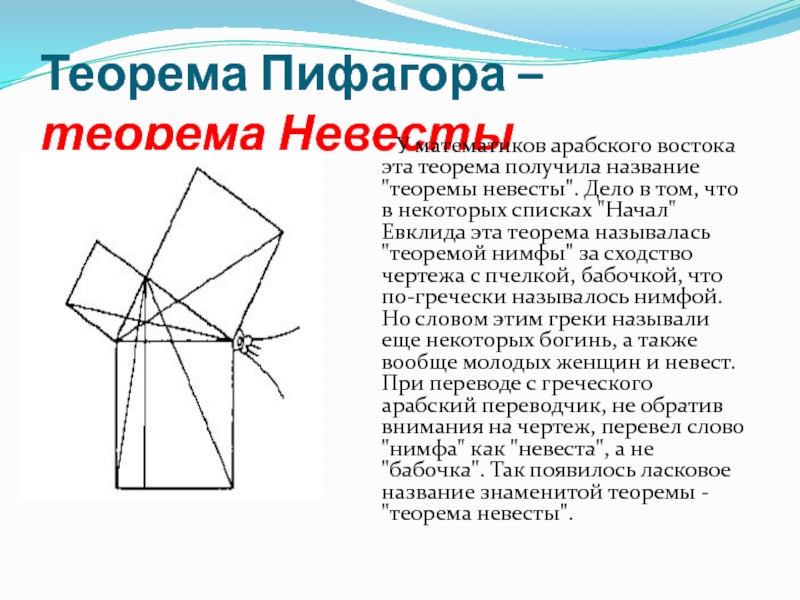
5. Теорема Пифагора – теорема Невесты
6. Теорема Пифагора у Евклида: В прямоугольном
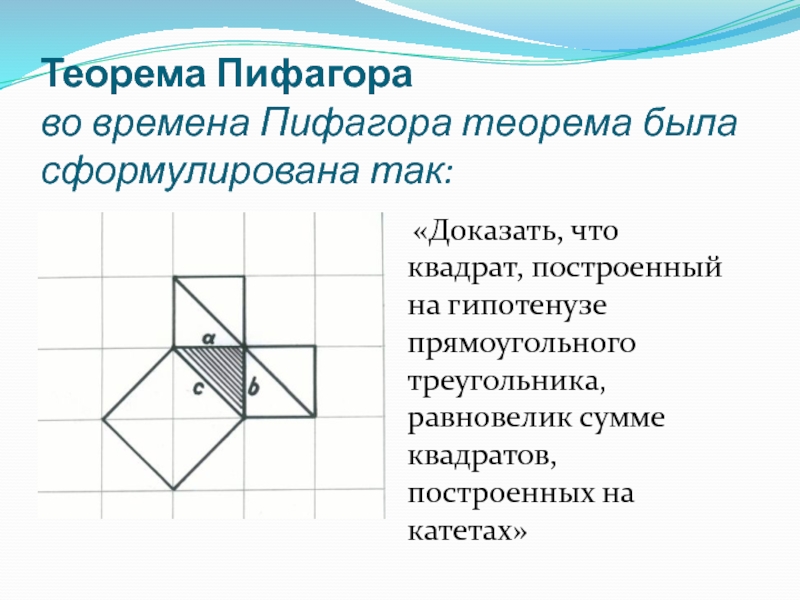
7. Теорема Пифагора во времена Пифагора теорема была
8. Латинский перевод: Во всяком прямоугольном треугольнике
9. Немецкий перевод: Итак, площадь квадрата, измеренного
10. Если дан нам треугольник, И притом
11. Долина устных задач
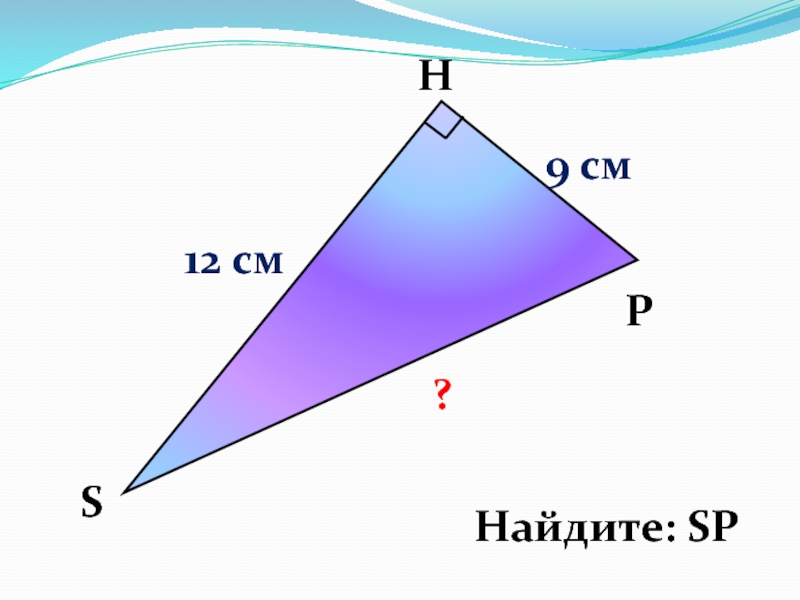
12. НS Р12 см9 см 15 см ?Найдите: SP
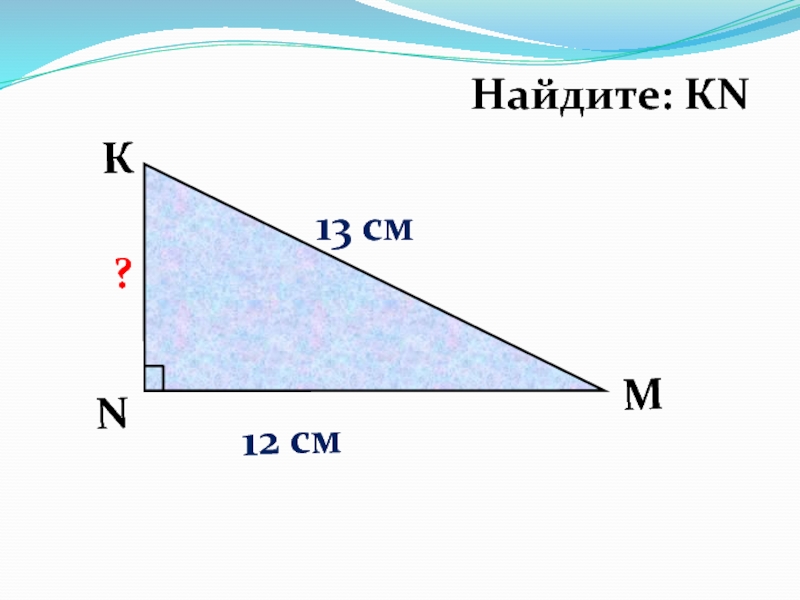
13. К?12 см13 cмN МНайдите: КN 5 cм
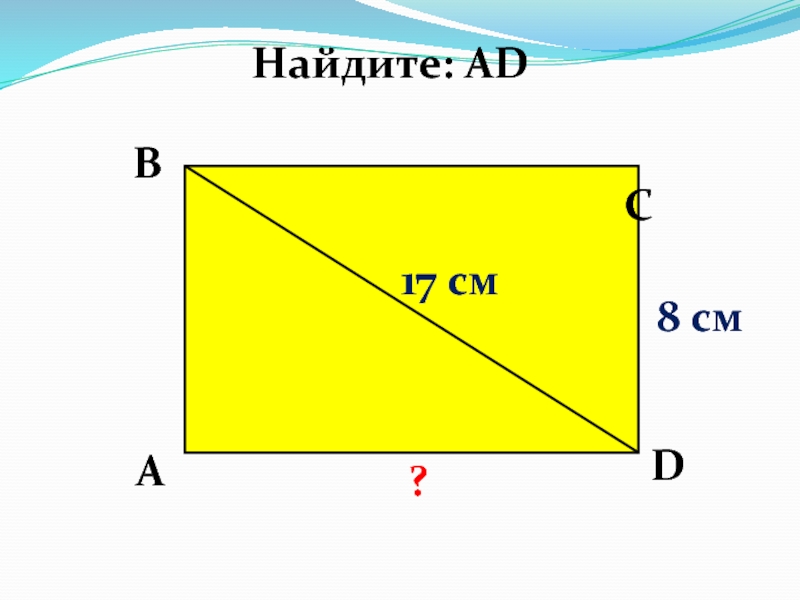
14. В? 8 см17 смА D СНайдите: АD 15 cм
15. Остров Незнаек
16. Задача № 1(индийского математика XII века Бхаскары)"На
17. Дано: АВС, ۦےС =
18. Из одной точки на земле отправились в
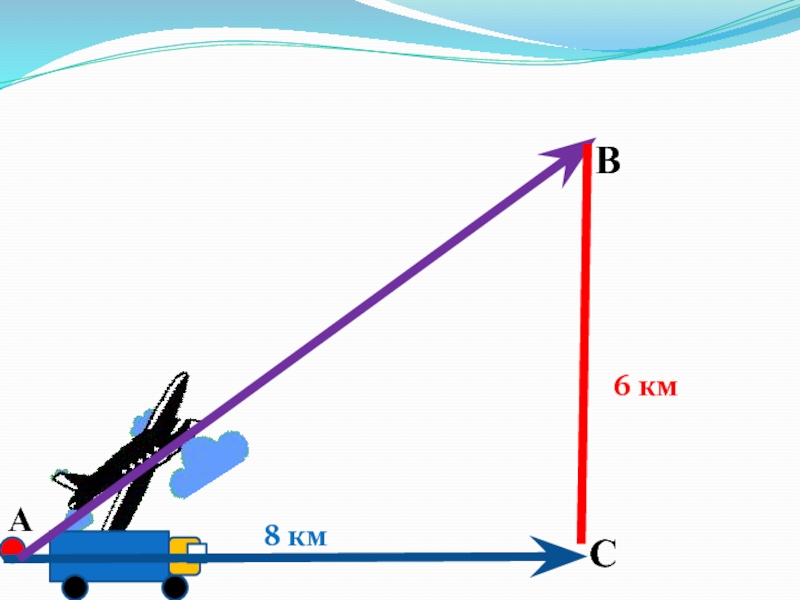
19. 8 км6 км? кмВСА
20. Дано: АВС, ۦےС
21. Задача № 498 (а – в) учебник
22. Полянка Здоровья
23. Слайд 23
24. «Штурмуем»Крепость Формул
25. Проверь друга!I вариантII вариант
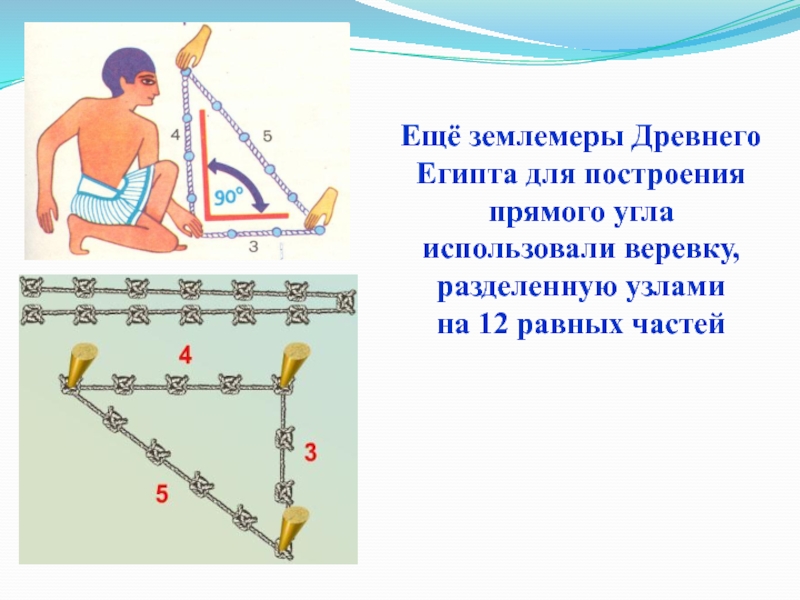
26. Ещё землемеры Древнего Египта для построения прямого угла использовали веревку, разделенную узлами на 12 равных частей
27. 25 и более баллов – оценка «5»18
28. Спасибо за урок!
29. Скачать презентанцию

«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора». Иоганн Кеплер

Главная
Математика
Применение теоремы Пифагора

Слайды и текст этой презентации

Слайд 1Теорема Пифагора
и её применение.

Слайд 2
«Геометрия владеет двумя сокровищами: одно из них – это теорема

Пифагора».
Иоганн Кеплер

Слайд 3Долина устных задач
Остров Незнаек
Полянка
Здоровья
Крепость Формул
Историческая тропинка

Слайд 4(580 - 500 г. до н.э.)
Пифагор

Слайд 5Теорема Пифагора – теорема Невесты
У математиков

арабского востока эта теорема получила название "теоремы невесты". Дело в

том, что в некоторых списках "Начал" Евклида эта теорема называлась "теоремой нимфы" за сходство чертежа с пчелкой, бабочкой, что по-гречески называлось нимфой. Но словом этим греки называли еще некоторых богинь, а также вообще молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимания на чертеж, перевел слово "нимфа" как "невеста", а не "бабочка". Так появилось ласковое название знаменитой теоремы - "теорема невесты".

Теорема Пифагора – теорема Невесты У математиков арабского востока эта теорема получила название

Слайд 6Теорема Пифагора у Евклида:
В прямоугольном треугольнике квадрат стороны,

натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой

угол

Слайд 7Теорема Пифагора во времена Пифагора теорема была сформулирована так:
«Доказать, что

квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных

на катетах»

Теорема Пифагора во времена Пифагора теорема была сформулирована так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,

Слайд 8Латинский перевод:
Во всяком прямоугольном треугольнике квадрат, образованный на

стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных

на двух сторонах, заключающих прямой угол

Латинский перевод: Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме

Слайд 9Немецкий перевод:
Итак, площадь квадрата, измеренного по длинной стороне,

столь же велика, как у двух квадратов, которые измерены по

двум сторонам его, примыкающим к прямому углу

Немецкий перевод: Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов,

Слайд 10 Если дан нам треугольник, И притом с прямым углом, То квадрат

гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим — И

таким простым путем, К результату мы придем.

Если дан нам треугольник, И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем:

Слайд 11Долина устных задач

Слайд 12Н
S
Р
12 см
9 см
15 см
?
Найдите: SP

Слайд 13К
?
12 см
13 cм
N
М
Найдите: КN
5 cм

Слайд 14В
?
8 см
17 см
А
D
С
Найдите: АD

15 cм

Слайд 15Остров Незнаек

Слайд 16Задача № 1
(индийского математика XII века Бхаскары)
"На берегу реки рос

тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И

угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?"