Применение теоремы синусов и косинусов

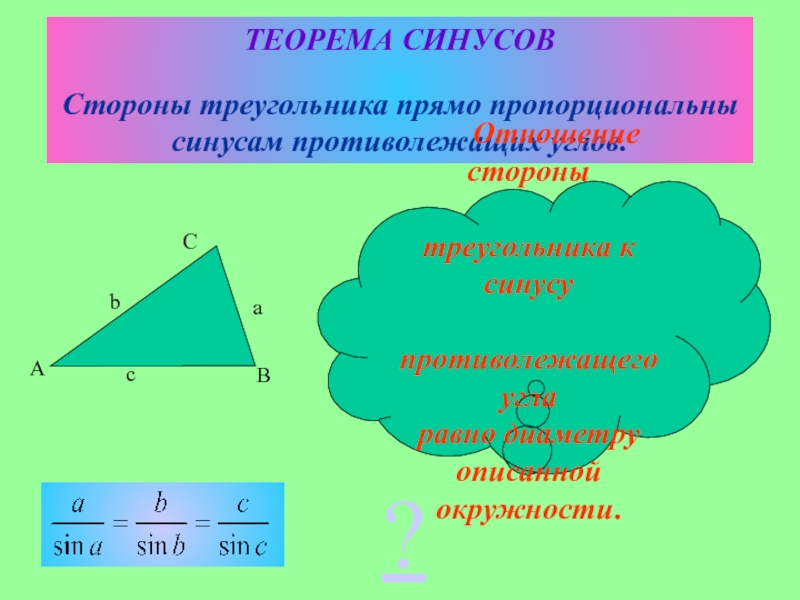
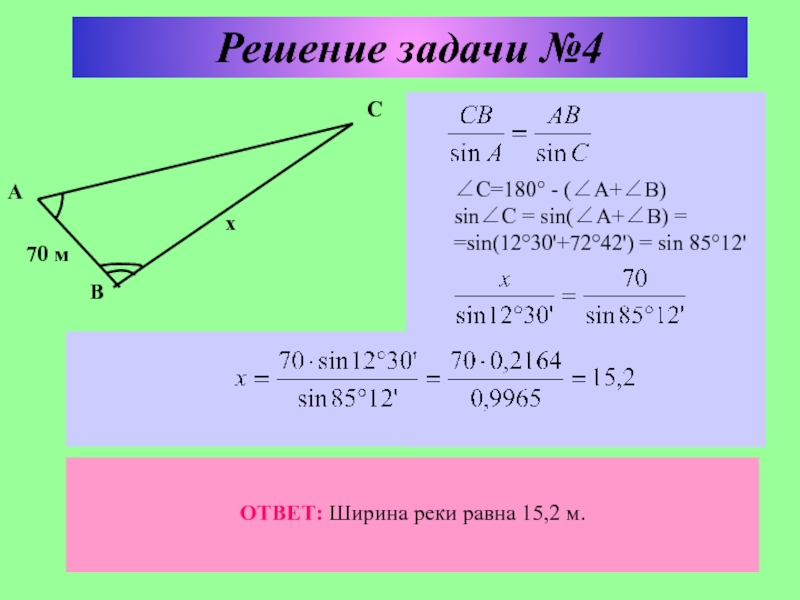
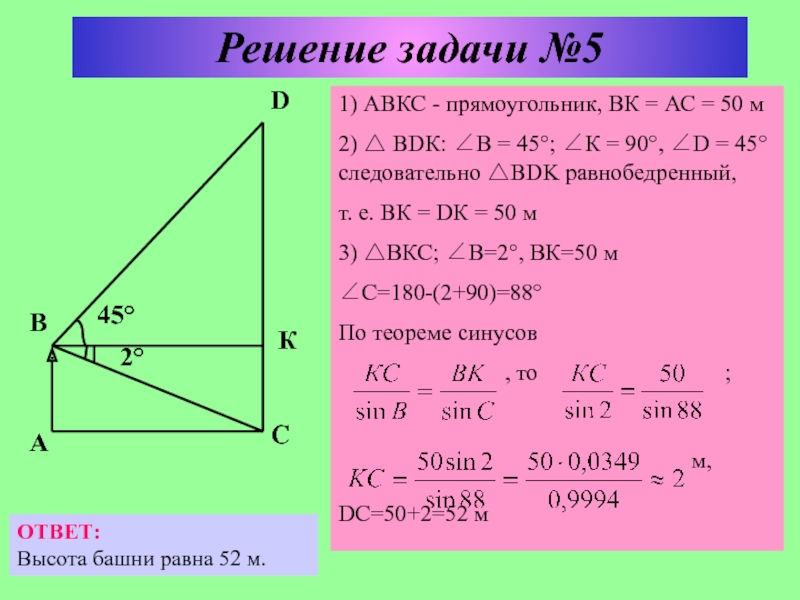
использовании теорем синусов и косинусов;
Развивающая:
Развивать внимание, речь, абстрактное и

логическое мышление учащихся
Воспитательная:
Формировать познавательную активность, дисциплинированность, ответственность, аккуратность и культуру поведения

ЦЕЛИ УРОКА:

Отношение стороны
треугольника к

синусу
противолежащего угла
равно диаметру
описанной
окружности.

?

ВС = 5 см, sinА =
Найти: sinС



Решение:

=> =>

минус удвоенное произведение этих сторон на косинус угла между ними.

а2 =b2 +c2 - 2bc cosA

Это частный
случай теоремы
Пифагора.
Почему?

?

ВС = 4 см, cosC =
Найти: AB



Решение:

ЗАДАЧИ

Произведем несколько измерительных работ на местности вместе, а остальные вы произведете самостоятельно в классе и дома

Задача №1

Задача №2

Задача №3

В классе №4

В классе №5

Д/З №15

Д/З №16

Д/З п. 109-112

и точки В и С в основаниях стоек ворот. По

условию задачи с = АВ = 23 м, b = АС = 24 м и а = ВС = 7 м. Эти данные позволяют решить треугольник АВС и найти угол α, равный углу А. С помощью теоремы косинусов определяем cosA:


Угол α находим по таблице: α ≈ 16°57′.

Решение задачи №1

Условие.
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и С стоек ворот (рис.1). Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.

1

1.

Для этого отметим точку В на определенном расстоянии α от

основания Н предмета и измерим угол АВН: ∠АВН=α. По этим данным из прямоугольного треугольника АВН находим высоту предмета: АН = а tgα.
Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии α друг от друга и измерим углы АВН и АСВ: ∠АВН=α и ∠АСВ=β(рис. 2). Эти данные позволяют определить все элементы треугольника АВС, в частности АВ. В самом деле, ∠АВН- внешний угол треугольника АВС, поэтому ∠А=α-β.
Используя теорему синусов, находим АВ:

Из прямоугольного треугольника АВН находим высоту АН предмета:
АН=АВ⋅sin α. Итак, АН=

Решение задачи №2
Измерение высоты предмета

до недоступного пункта С (рис. 3). Напомним, что эту задачу

мы уже решали в 8 классе с помощью признаков подобия треугольников. Рассмотрим теперь другой способ решения задачи – с использованием формул тригонометрии.
На местности выберем точку В и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В: ∠А=α и ∠В=β. Эти данные, т. е. с, α и β, позволяют решить треугольник АВС и найти искомое расстояние d=AC.
Сначала находим ∠С=180°-α-β,
Sin С = sin(180°-α-β)=sin(α+β).
Затем с помощью теоремы синусов находим d. Так как ,

АС=d, AB=c, ∠B=β, то d= .

Решение задачи №3
Измерение расстояния до недоступной точки

3

А и В на берегу реки на расстоянии 70 м

друг от друга и измерили углы САВ и АВС, где С – дерево, стоящее на другом берегу у кромки воды. Оказалось, что ∠САВ=12°30′, ∠АВС=72°42′. Найдите ширину реки.

х

?

sin 85°12'









A
B
C
70 м

х




ОТВЕТ: Ширина реки равна 15,2 м.

высоту которой хочет определить. Основание башни он видит под углом

2° к горизонту, а вершину – под углом 45° к горизонту. Какова высота башни?

?

50 м
2) △ ВDК: ∠В = 45°; ∠К = 90°,

∠D = 45° следовательно △ВDK равнобедренный,
т. е. ВК = DК = 50 м
3) △ВКС; ∠В=2°, ВК=50 м
∠С=180-(2+90)=88°
По теореме синусов
, то ;

м,

DС=50+2=52 м

ОТВЕТ:
Высота башни равна 52 м.