Применение теории графов к решению задач

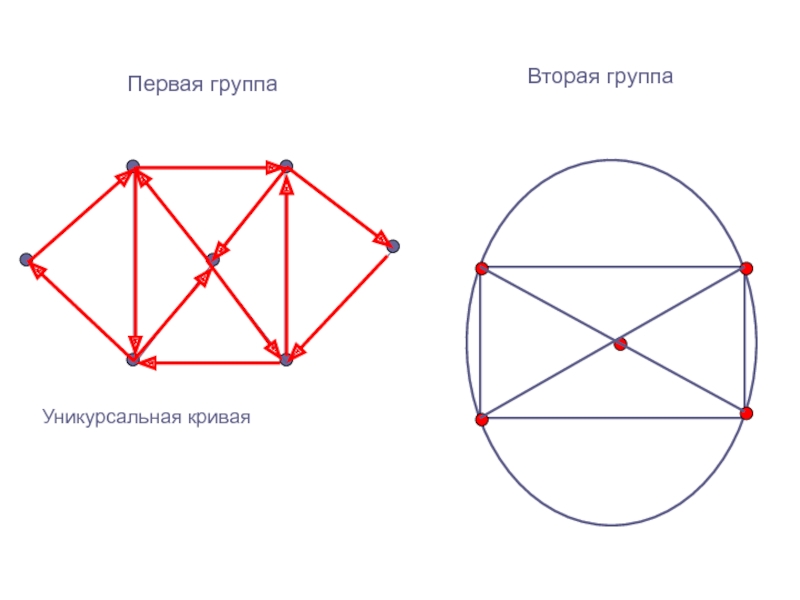
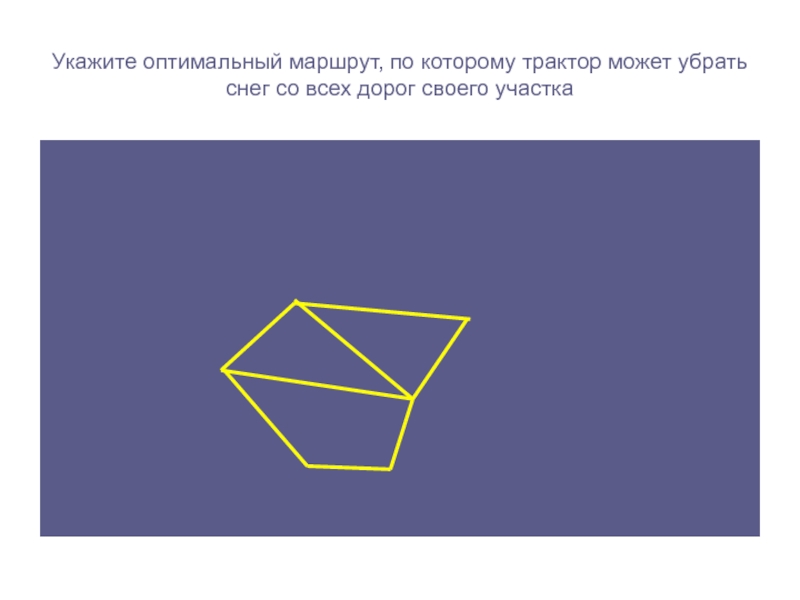
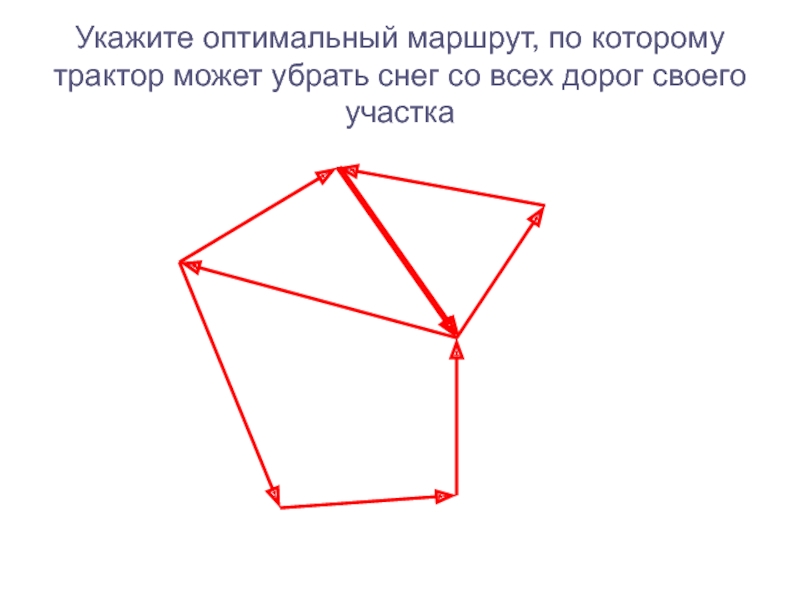
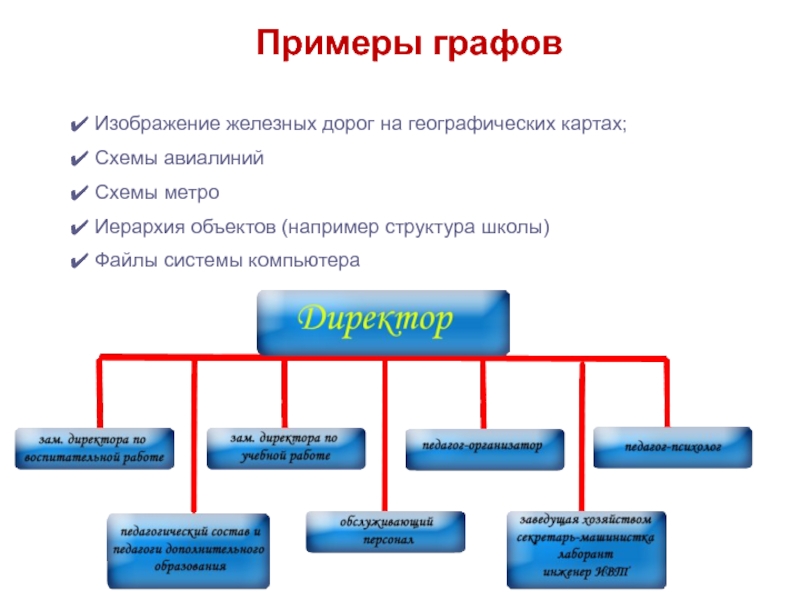
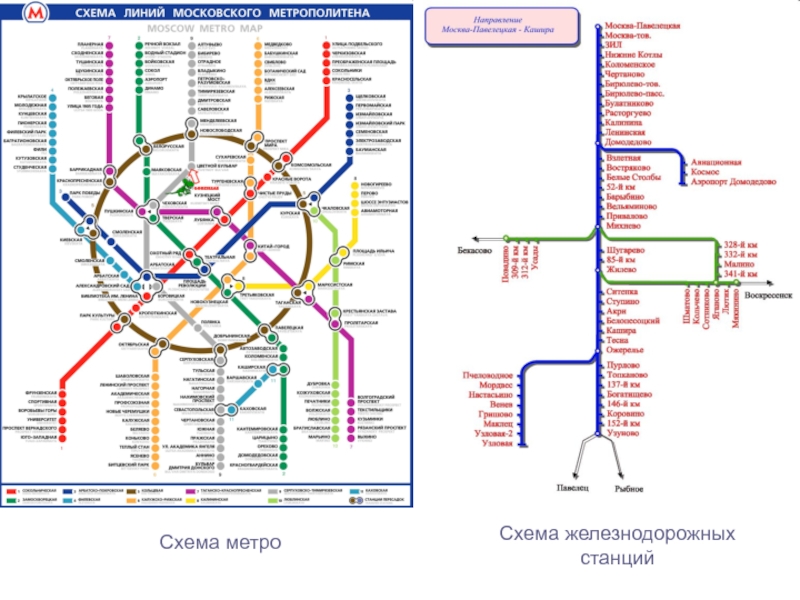
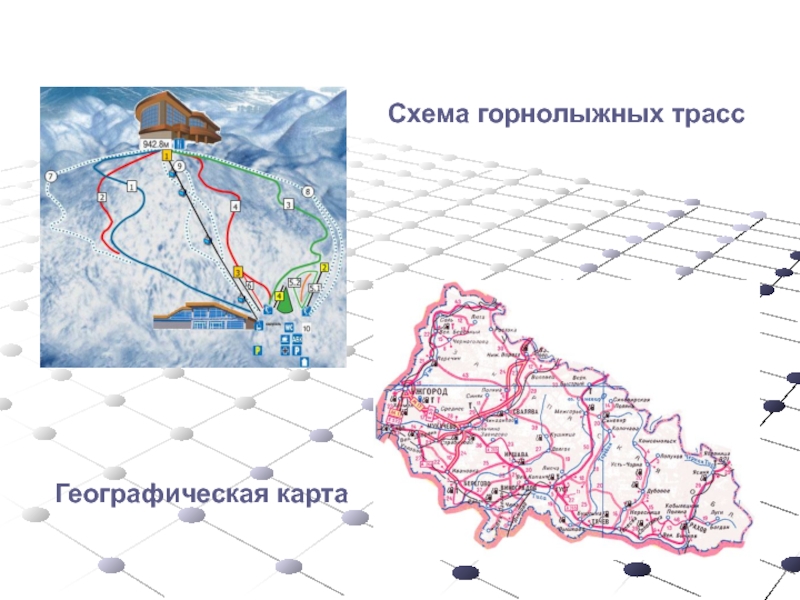
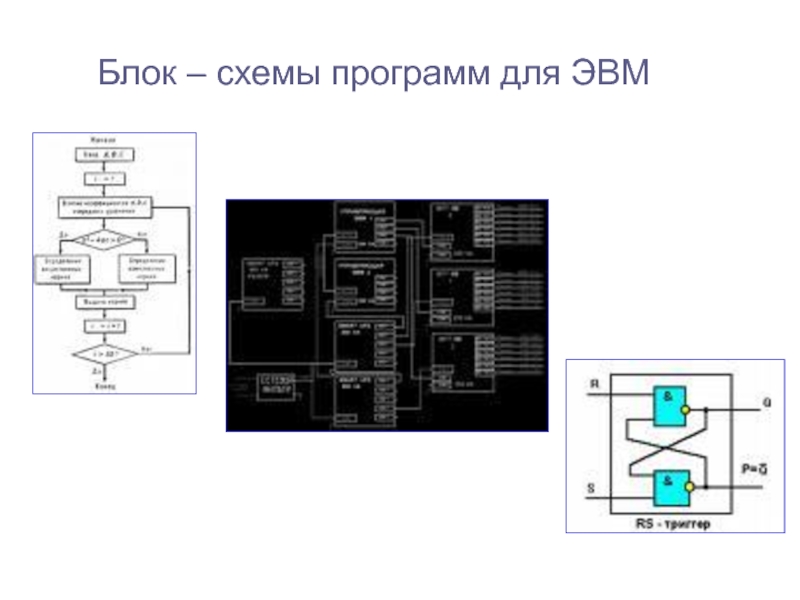
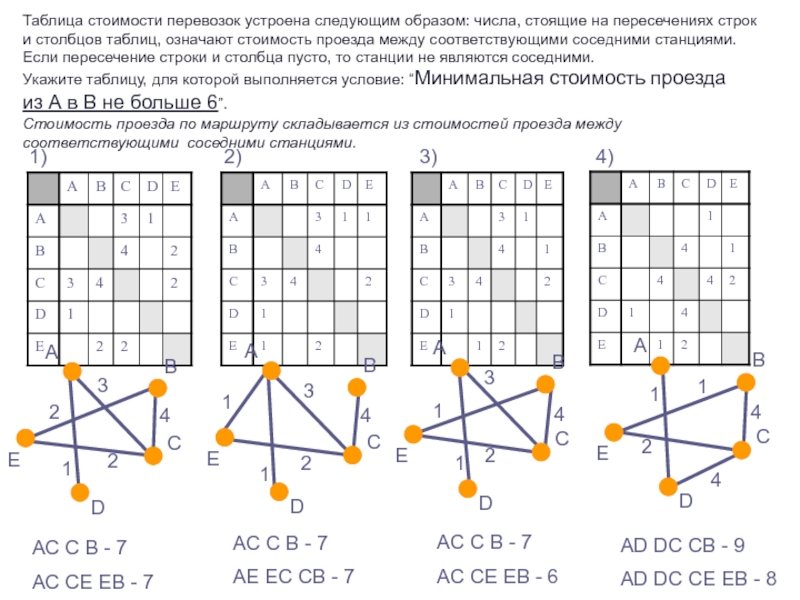
следующие СВОЙСТВА графа:
Если в фигуре только четные вершины ,

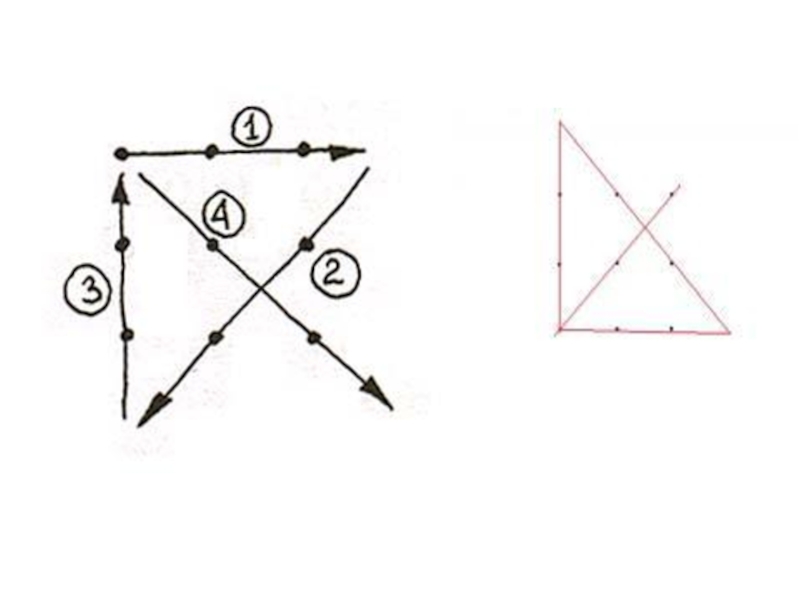
то ее можно нарисовать одним росчерком, независимо от того, с какого места начинается черчение.

2) Если в фигуре имеется только одна пара нечетных вершин, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных вершин.

3) Если фигура имеет более одной пары нечетных вершин, то она вовсе не может быть нарисована одним росчерком.
В задаче о семи Кенигсбергских мостах все четыре вершины соответствующего графа - нечетные, т.е. нельзя пройти по всем мостам ровно один раз и закончить путь там, где он был начат.

про Кенигсбергские мосты, он вывел еще два СВОЙСТВА:
4)

Число нечетных вершин графа всегда четно.
5) Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.


Например, если фигура имеет четыре нечетные вершины, то ее можно начертить самое меньшее двумя росчерками.

геометрическая фигура, как начертить ее на бумаге одним росчерком пера,

не проводя дважды ни одну линию?


Например: как проложить дорожки в дендропарке, чтобы посетители увидели все растения не проходя дважды по одной.

всех дорог своего участка

всех дорог своего участка

авиалиний
Схемы метро
Иерархия объектов (например структура школы)

Файлы системы компьютера

рабочих;
для расчетов устойчивости откоса
В физике
Анализ электрических цепей распознаётся методом графов,

также применяется в классической электродинамике СТО, энергетике, радиоэлектронике и др.
В химии
Используется для составления формул
Для исследования стационарной кинетически ферментативных реакций

(геоботаника)
Метод графов при составлении дихотомических ключей для определения

растений.
Транспорт
Для расчета пассажиропотока
Медицина
Исследование биоритмов
Биология
Для анализа биологических структур и генных систем
Спорт
Разработка стратегии игры

и ОГЭ:

были приглашены 4 врача. Каждый из приглашенных работал в 2

поликлиниках и представлял на этом совещании обе поликлиники. Любая возможная комбинация двух поликлиник имело на этом совещании одного и только одного представителя. Сколько поликлиник в городе? Сколько врачей было приглашено на совещание?

Задача

Ответ: 5 поликлиник;
10 врачей.

в пункт можно только в направлении стрелок. В каждом пункте

можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из путей наименьшая длина? У какого наибольшая длина?

продолжительного пути 7: 1 2 3 6 5 7 8

9.
Число путей 14

Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу? Дорожки не могут

проходить через колодцы и домики.

кучки камней, в первой из которых 3, а во второй

– 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

3,18, ∑ 21

3,2, ∑ 5

строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними

станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “Минимальная стоимость проезда
из А в B не больше 6”.
Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

1)

2)

3)

4)

AC C B - 7
AC CE EB - 7

AC C B - 7
AE EC CB - 7

AC C B - 7
AC CE EB - 6

AD DC CB - 9
AD DC CE EB - 8

нет
2. На занятии мне понравилось:
история графов

практические задания
3. Я применю это в своей практике да нет