Слайд 1Признаки
параллельности двух прямых
Зачетная
работа
Слайд 21. Отметь знаком «+» правильные утверждения
и знаком «-» —
ошибочные.
1. Параллельными прямыми называются прямые, которые не пересекаются.
2. Параллельными прямыми
называются прямые, лежащие на плоскости и не пересекающиеся.
3. Параллельных прямых можно провести только 2.
4. Параллельных прямых можно провести только 3.
5. Параллельных прямых можно провести сколько угодно.
6. Если некоторая прямая пересекает одну из 2-x параллельных прямых, то она может пересечь и другую.
7. Через любую точку, не лежащую на данной прямой, можно провести
в плоскости параллельную ей прямую, и только одну.
8. Если 2 прямые параллельны третьей, то они не могут быть параллельными.
Слайд 3Отметь знаком «+» правильные утверждения
и знаком «-» — ошибочные.
9.
Если 2 прямые параллельны III, то они могут быть параллельными.
10.
Если 2 прямые параллельны III, то они параллельны между собой.
11. Если 2 прямые перпендикулярны III, то они не могут быть параллельными.
12. Если 2 прямые перпендикулярны III, то они не могут быть перпендикулярными между собой.
13. Если 2 прямые перпендикулярны III, то они могут быть параллельными.
14. Если 2 прямые перпендикулярны III, то они могут быть перпендикулярными между собой.
15. Если 2 прямые перпендикулярны III, то они параллельны.
16. Если 2 прямые перпендикулярны III, то они перпендикулярны.
Слайд 42. Выбери правильный вариант ответа.
1. Две прямые называются параллельными, если
они
а) не пересекаются;
б) лежат на одной плоскости и не пересекаются;
в) лежат на одной
плоскости и пересекаются.
2. Параллельных прямых можно провести только
а) только 2; б) только 3;
в) сколько угодно.
3. Если 2 прямые на плоскости параллельны III, то они
а) параллельны между собой;
б) могут быть параллельны;
в) не могут быть параллельны.
4. Если 2 прямые на плоскости перпендикулярны III, то они
а) перпендикулярны между собой;
б) параллельны между собой
в) они не могут быть ни параллельными, ни перпендикулярными между собой.
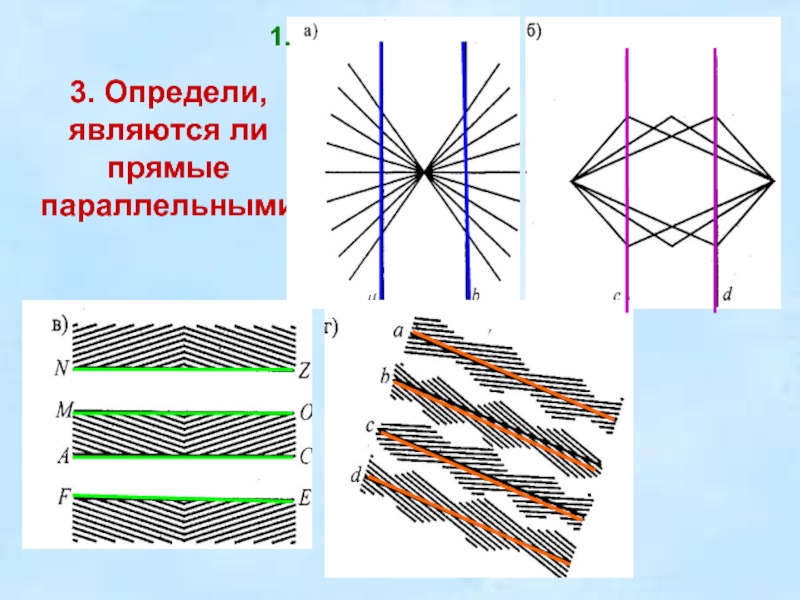
Слайд 53. Определи,
являются ли
прямые
параллельными
1.
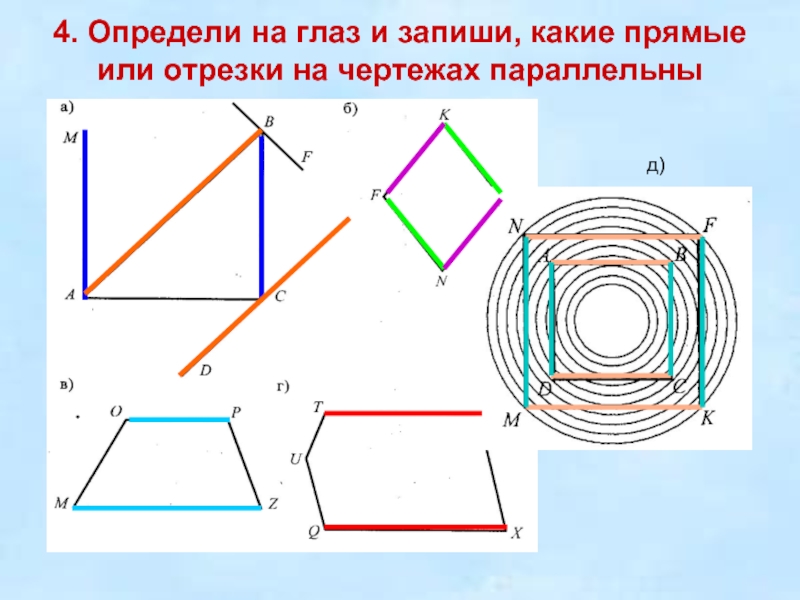
Слайд 64. Определи на глаз и запиши, какие прямые или отрезки
на чертежах параллельны
д)
Слайд 75. Начерти прямую ХУ. Через 3 произвольные точки M, N
и К этой прямой с помощью угольника проведи прямые MA
|| NB || КС.
6. Построй произвольный треугольник ABC и произвольную точку М Є АВС. Через точку М проведи 3 прямые: MN || АВ, MX || AC,MY || BC.
7. Начерти четырехугольник, у которого:
а) две пары параллельных сторон;
б) одна пара параллельных сторон;
в) нет параллельных сторон.
8. Даны 5 прямых: а, Ь, с, d, е, причем а || Ь, Ь || с,
с || d, d || е. Докажи, что а || е.
9. Даны прямые а, Ь, с, d. Известно, что а || Ь, с a,
d Ь. Сделай вывод о взаимном расположении прямых c u d.
Слайд 810. Блиц-опрос: Закончи предложение
1. Параллельными называются прямые ...
2. Два отрезка называются
параллельными, если ...
3. Если прямая пересекает одну из параллельных прямых, то
она
(пересекает, не пересекает) другую.
4. Если 2 прямые параллельны III, то ...
5. Через любую точку, не лежащую на данной прямой, можно провести ... прямых, параллельных данной.
6. Если 2 прямые перпендикулярны III, то они ... между собой.
Слайд 911. Закончи предложение
1. Прямая х называется секущей по отношению к
прямым а и b, если ...
2. При пересечении двух прямых
секущей образуется ... неразвернутых углов.
3. Если прямые АВ и CD пересечены прямой BD,
то прямая BD называется ...
Слайд 1011. Закончи предложение
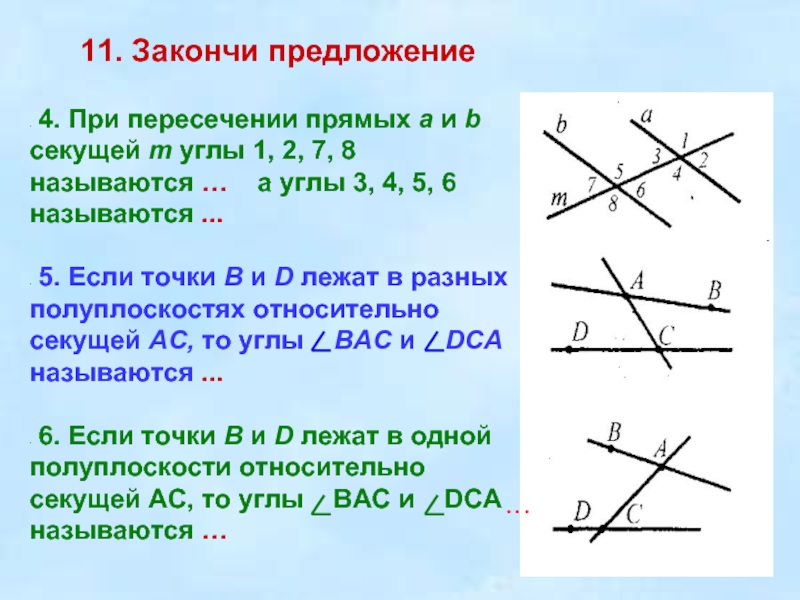
4. При пересечении прямых а и b
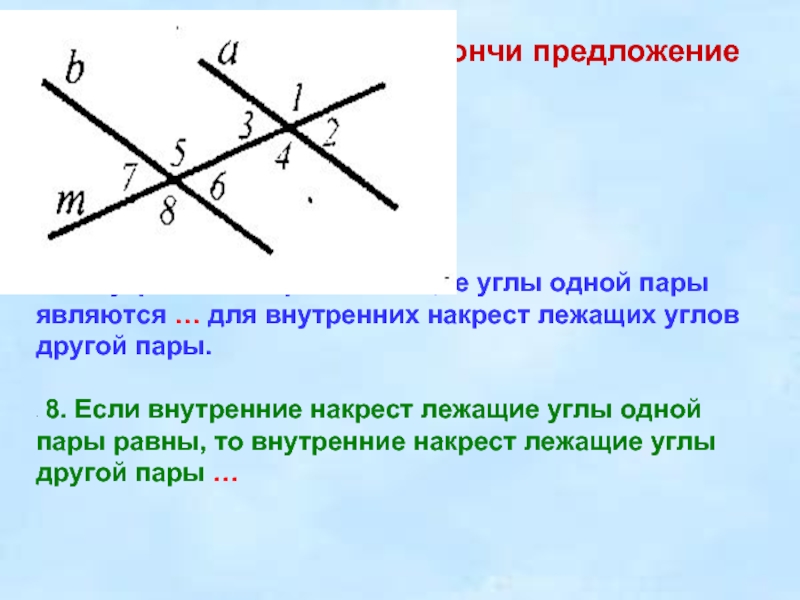
секущей т углы 1, 2, 7, 8 называются …
а углы 3, 4, 5, 6 называются ...
5. Если точки В и D лежат в разных полуплоскостях относительно секущей АС, то углы ВАС и DCА называются ...
6. Если точки В и D лежат в одной полуплоскости относительно секущей AC, то углы BAC и DCA
называются …
Слайд 1111. Закончи предложение
7. Внутренние накрест лежащие углы одной пары
являются … для внутренних накрест лежащих углов другой пары.
8.
Если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары …
Слайд 1212. Отметь знаком «+» правильные утверждения и знаком «-» —
ошибочные.
* 1. При пересечении 2 прямых III образуется 4 неразвернутых
угла.
* 2. При пересечении 2 прямых III образуется 8 неразвернутых углов.
* 3. Углы 1, 2, 7, 8 называются внутренними.
* 4. Углы 1, 2, 7, 8 называются внешними.
* 5. Углы 3, 4, 5, 6 называются внутренними.
* 6. Углы 3, 4, 5, 6 называются внешними.
* 7. Углы 3 и 5, 4 и 6 называются внутренними накрест лежащими.
Слайд 1312. Отметь знаком «+» правильные утверждения и знаком «-» —
ошибочные.
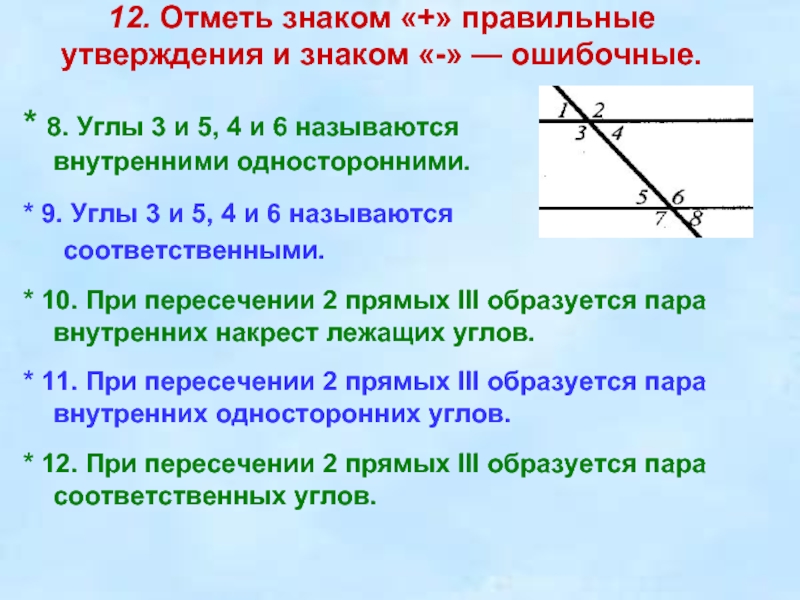
* 8. Углы 3 и 5, 4 и 6 называются
внутренними односторонними.
* 9. Углы 3 и 5, 4 и 6 называются
соответственными.
* 10. При пересечении 2 прямых III образуется пара внутренних накрест лежащих углов.
* 11. При пересечении 2 прямых III образуется пара внутренних односторонних углов.
* 12. При пересечении 2 прямых III образуется пара соответственных углов.
Слайд 1412. Отметь знаком «+» правильные утверждения
и знаком «-» —
ошибочные.
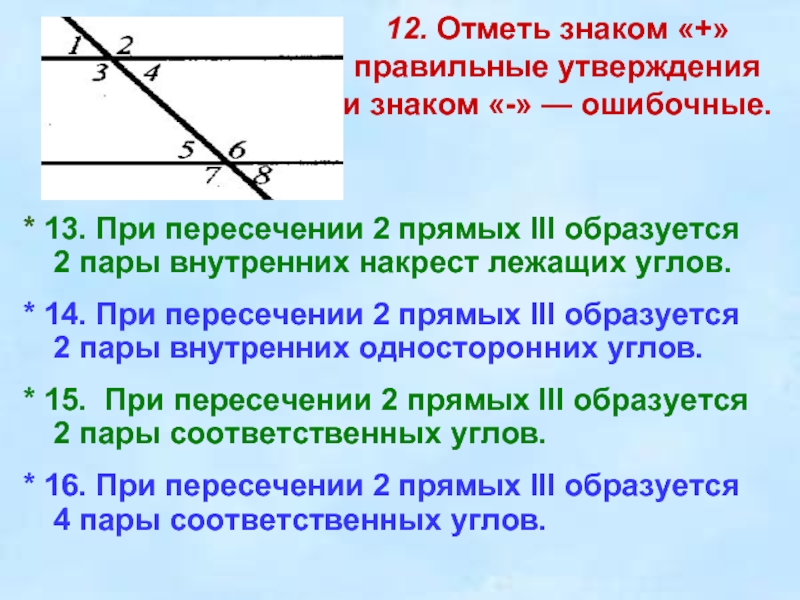
* 13. При пересечении 2 прямых III образуется 2 пары
внутренних накрест лежащих углов.
* 14. При пересечении 2 прямых III образуется 2 пары внутренних односторонних углов.
* 15. При пересечении 2 прямых III образуется 2 пары соответственных углов.
* 16. При пересечении 2 прямых III образуется 4 пары соответственных углов.
Слайд 1513. Выбери правильный вариант ответа.
1. При пересечении 2 прямых секущей
образуется:
а) 4 угла;
б) 8 углов;
в) 10 углов.
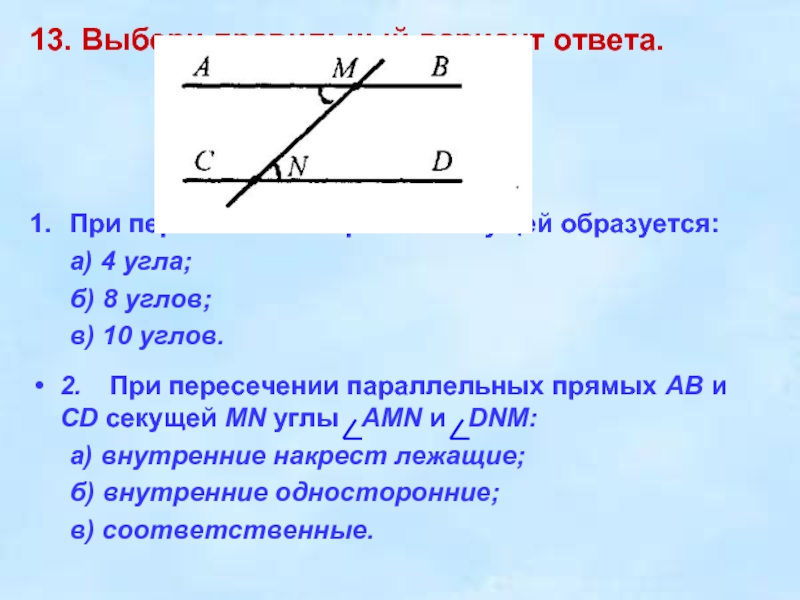
2. При пересечении параллельных прямых
АВ и CD секущей MN углы AMN и DNM:
а) внутренние накрест лежащие;
б) внутренние односторонние;
в) соответственные.
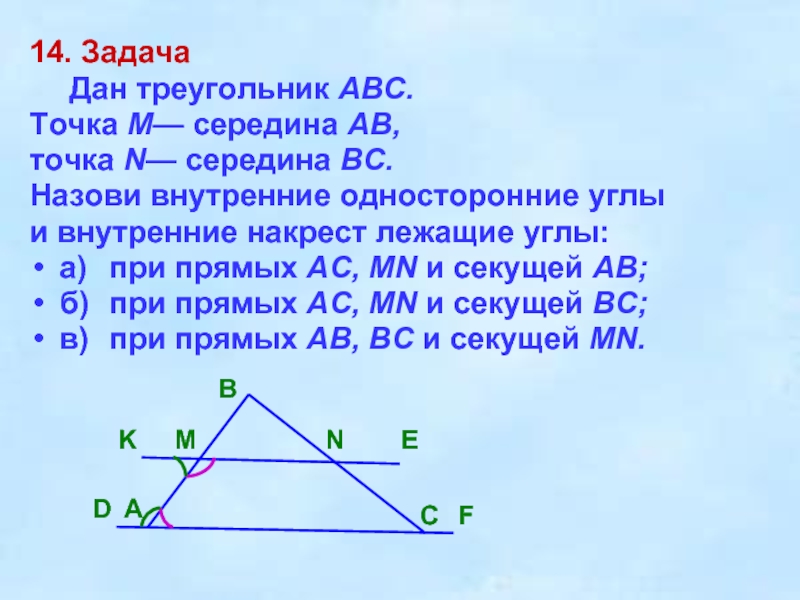
Слайд 1614. Задача
Дан треугольник ABC.
Точка М— середина АВ,
точка N—
середина ВС.
Назови внутренние односторонние углы
и внутренние накрест лежащие
углы:
а) при прямых AC, MN и секущей АВ;
б) при прямых AC, MN и секущей ВС;
в) при прямых АВ, ВС и секущей MN.
D
F
K
E
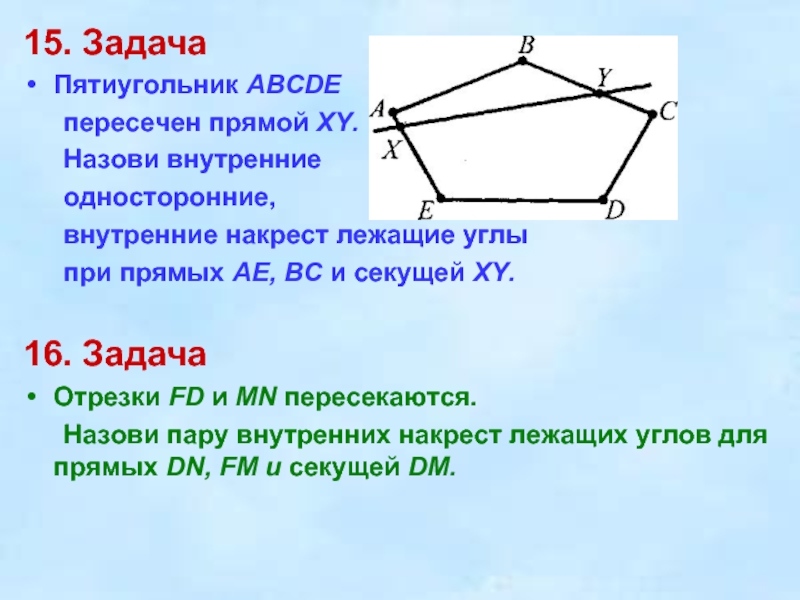
Слайд 1715. Задача
Пятиугольник ABCDE
пересечен прямой XY.
Назови внутренние
односторонние,
внутренние
накрест лежащие углы
при прямых АЕ, ВС и секущей XY.
16.
Задача
Отрезки FD и MN пересекаются.
Назови пару внутренних накрест лежащих углов для прямых DN, FM и секущей DM.
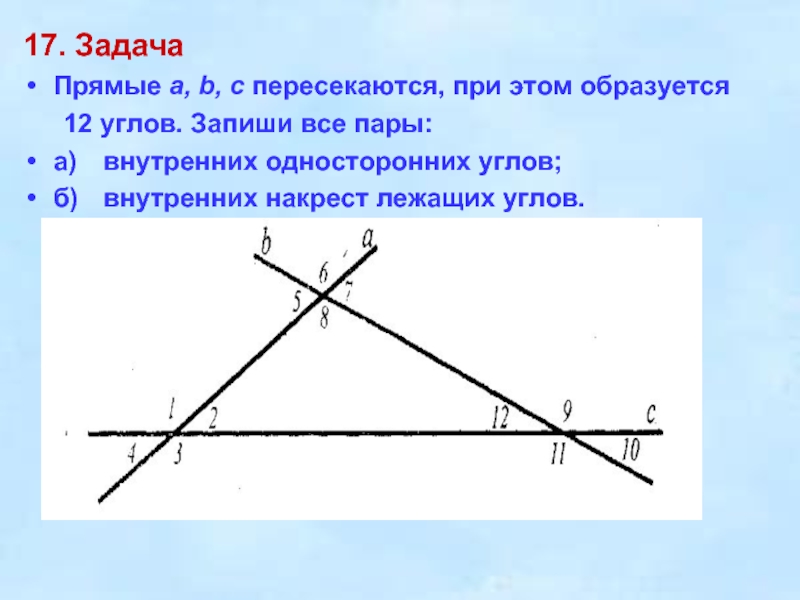
Слайд 1817. Задача
Прямые а, b, с пересекаются, при этом образуется
12
углов. Запиши все пары:
а) внутренних односторонних углов;
б) внутренних накрест лежащих углов.
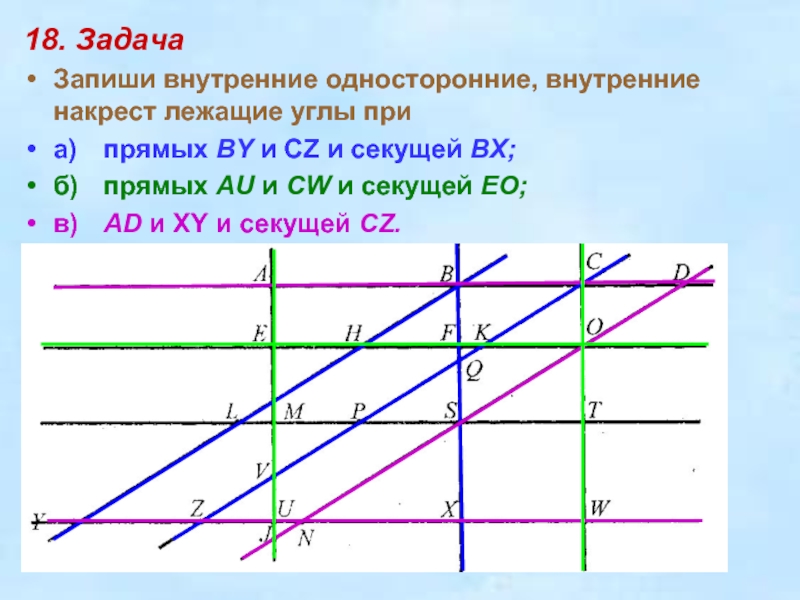
Слайд 1918. Задача
Запиши внутренние односторонние, внутренние накрест лежащие углы при
а) прямых BY
и CZ и секущей ВХ;
б) прямых AU и CW и секущей
EO;
в) AD и XY и секущей CZ.
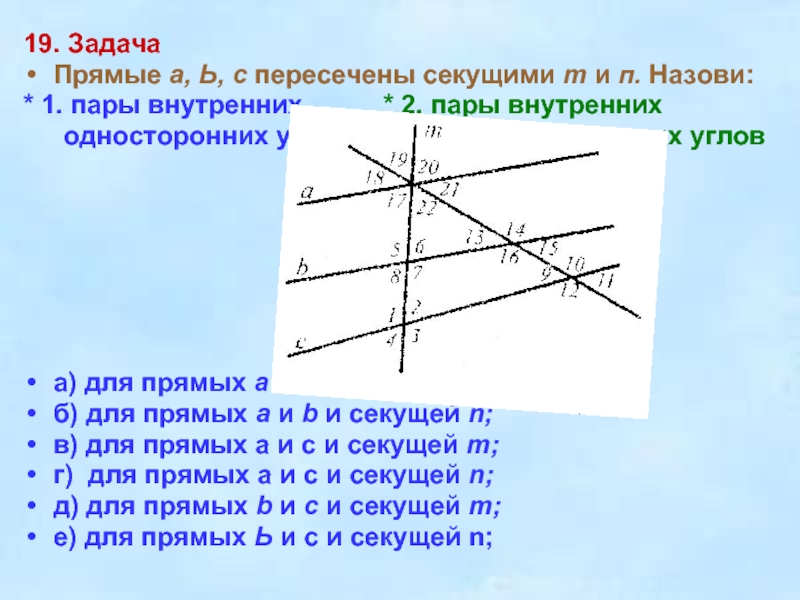
Слайд 2019. Задача
Прямые а, Ь, с пересечены секущими т и п.
Назови:
* 1. пары внутренних * 2. пары внутренних
односторонних углов
накрест лежащих углов
a) для прямых а и b и секущей т;
б) для прямых а и b и секущей n;
в) для прямых а и с и секущей т;
г) для прямых а и с и секущей n;
д) для прямых b и с и секущей т;
е) для прямых Ь и с и секущей n;
Слайд 2120. Задача
В четырехугольнике ABCD
A = 52°, B
= 128°, С= 56°.
Параллельны ли стороны АВ и CD?
Параллельны ли стороны AD и ВС?
Обоснуй свои выводы.
21. Задача
Докажи,что
в четырехугольнике ABCD АВ||CD, AD||ВС.
22. Задача
Отрезки АВ и CD пересекаются в точке О,
которая является серединой каждого из них.
Докажи,что прямые АС и BD параллельны.
Слайд 2223. Задача
Выбери неправильный вариант ответа.
1. Две прямые называются параллельными, если
а) они
не пересекаются;
б) лежат в одной плоскости и не пересекаются.
2. Соответственные углы всегда
равны при
а) двух прямых и секущей;
б) двух параллельных и секущей.
3. Прямые АВ и CD
пересечены секущей MN,
причем MND = 70°,
AMF= 110°.
Значит, а) AB||CD;
б) AB || СD
Слайд 2323. Задача
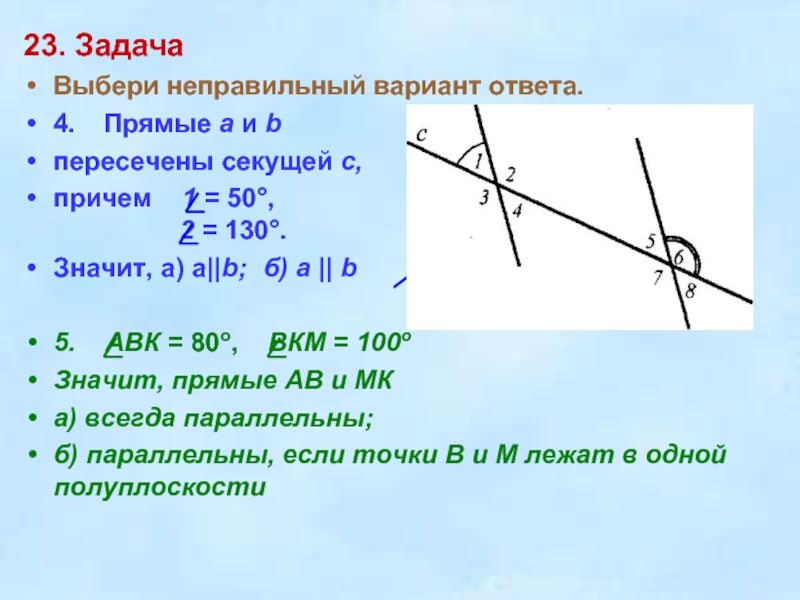
Выбери неправильный вариант ответа.
4. Прямые a и b
пересечены
секущей c,
причем 1 = 50°,
2 = 130°.
Значит, а) a||b; б) a || b
5. ABК = 80o, BКM = 100о
Значит, прямые АВ и МК
а) всегда параллельны;
б) параллельны, если точки В и М лежат в одной полуплоскости
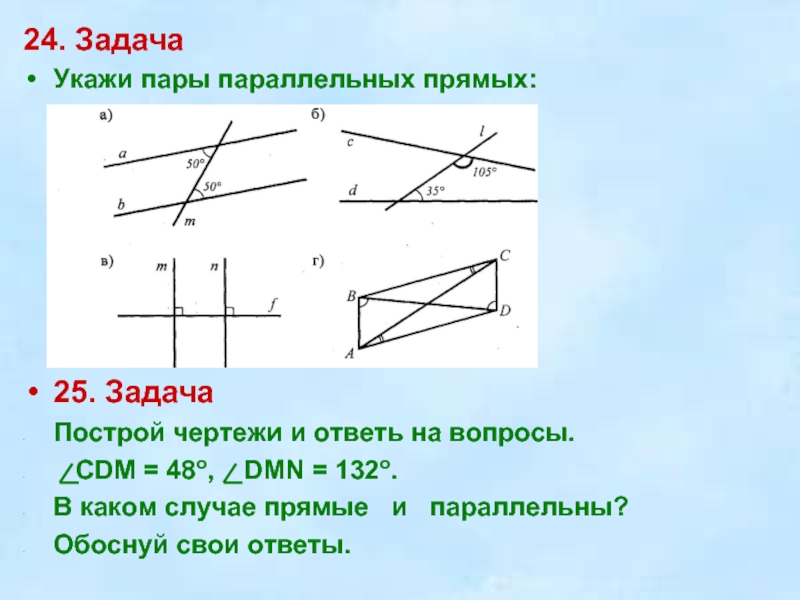
Слайд 2424. Задача
Укажи пары параллельных прямых:
25. Задача
Построй чертежи и ответь на
вопросы.
СDM = 48o, DMN = 132o.
В
каком случае прямые и параллельны?
Обоснуй свои ответы.
Слайд 2526. Задача
Диагонали АС и BD четырехугольника ABCD пересекаются в точке
О и делятся ею пополам. Докажи, что АВ||CD, ВС||AD.
27. Задача
Докажи,
что биссектрисы внутренних накрест лежащих углов BMN и CNM, образованных при пересечении параллельных прямых АВ и CD секущей ML, параллельны.
28. Задача
Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Являются ли отрезки AD и ВС параллельными?
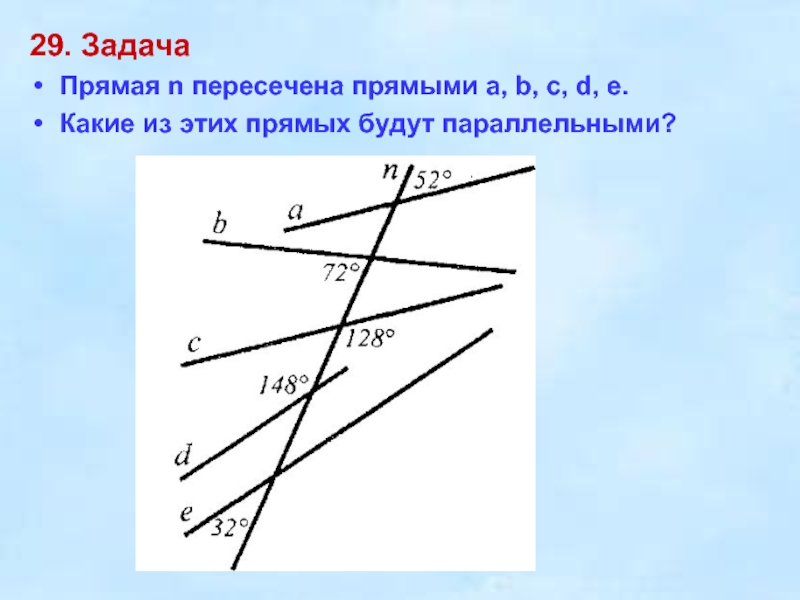
Слайд 2629. Задача
Прямая n пересечена прямыми a, b, c, d, e.
Какие из этих прямых будут параллельными?
Слайд 27 30. Задачки для любознательных
1. Доказать, что
две прямые параллельны, если параллельны прямые, перпендикулярные данным.
2. Пусть АВ||CD,
АВ=CD и точки В и С лежат по разные стороны прямой AD.
Доказать, что AC||BD и AC=BD.
3* Докажи, что две параллельные прямые высекают на двух других параллельных прямых равные отрезки. Могут ли этим свойством обладать две пересекающиеся прямые?
А. Александров, А. Вернер, В. Рыжик
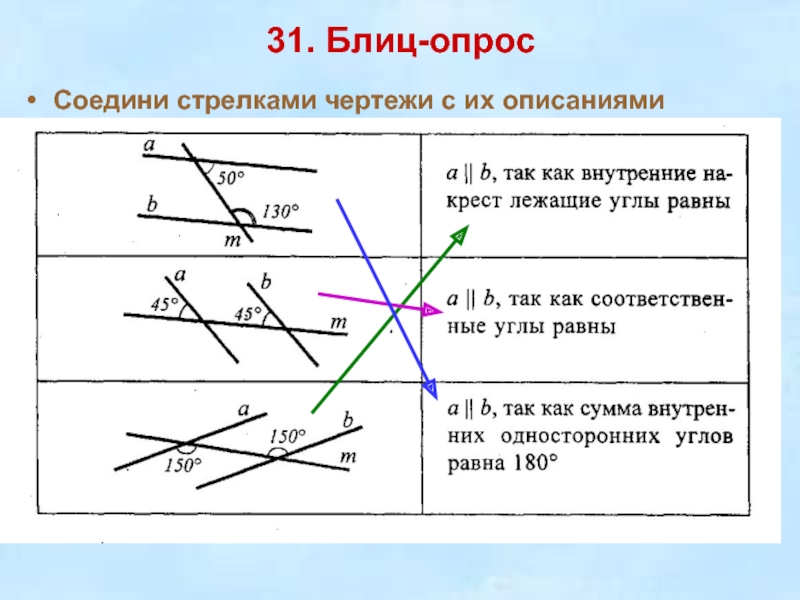
Слайд 2831. Блиц-опрос
Соедини стрелками чертежи с их описаниями