TheSlide.ru

Производная функции

Содержание

1. Производная функции
2. О происхождении терминов и обозначений производной и
3. «Алгоритм нахождения производной»
4. Геометрический смысл производной состоит в том, что
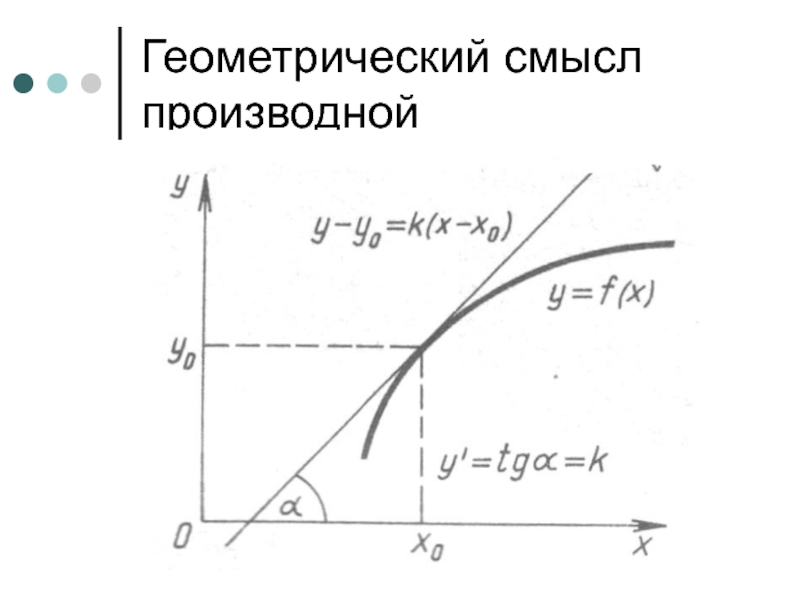
5. Геометрический смысл производной
6. Физический смысл Физический смысл скорость ускорениеПроизводная от перемещения по
7. Правила дифференцирования 1).Производная суммы равна сумме производных,
8. Найти производные:
9. 4).Производная частного:
10. Вычислить производную:
11. Найти производные функций:
12. Скачать презентанцию

О происхождении терминов и обозначений производной и пределаТермин «производная» - буквально перевод французского слова derivee.1797г – Ж.Лагранж ввел современные обозначения И.Ньютон называл производную флюксией, а саму функцию – флюентой.Г.Лейбниц говорил о

Слайды и текст этой презентации

Слайд 1Что называется производной?
Производной функции в данной точке называется предел отношения

приращения функции в этой точке к приращению аргумента, когда приращение

аргумента стремится к нулю.

Что называется производной?Производной функции в данной точке называется предел отношения приращения функции в этой точке к приращению

Слайд 2О происхождении терминов и обозначений производной и предела
Термин «производная» -

буквально перевод французского слова derivee.
1797г – Ж.Лагранж ввел современные обозначения

И.Ньютон называл производную флюксией, а саму функцию – флюентой.
Г.Лейбниц говорил о дифференциальном отношении и обозначал производную как

Термин «предел» (lim – сокращение латинского слова limes (межа, граница)) ввел И.Ньютон.

О происхождении терминов и обозначений производной и пределаТермин «производная» - буквально перевод французского слова derivee.1797г – Ж.Лагранж

Слайд 3«Алгоритм нахождения производной»

«Алгоритм нахождения производной»

Слайд 4Геометрический смысл производной состоит в том, что значение производной функции

y=f(x) в точке x равно угловому коэффициенту касательной к графику

функции в точке с абсциссой x:

Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке x равно угловому коэффициенту

Слайд 5Геометрический смысл производной

Геометрический смысл производной

Слайд 6Физический смысл
Физический смысл
скорость
ускорение
Производная от перемещения по времени является мгновенная скорость.
Производная

от скорости по времени является ускорением.

Физический смысл Физический смысл скорость ускорениеПроизводная от перемещения по времени является мгновенная скорость.Производная от скорости по времени является ускорением.

Слайд 7Правила дифференцирования
1).Производная суммы равна сумме производных, производная разности равна разности

производных: (f(x) ± g(x))'= f '(x) ±g '(x)
2).Постоянный множитель можно вынести

за знак производной: (Сf (x))'=Сf '(x)
3).Производная произведения: (f(x)g(x)) '=f '(x)g(x) + f(x)g '(x)

Правила дифференцирования 1).Производная суммы равна сумме производных, производная разности равна разности производных: (f(x) ± g(x))'= f '(x)

Слайд 8Найти производные:

Найти производные:

Слайд 94).Производная частного:

4).Производная частного:

Слайд 10Вычислить производную:

Вычислить производную:

Слайд 11Найти производные функций:

Найти производные функций:

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей