Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
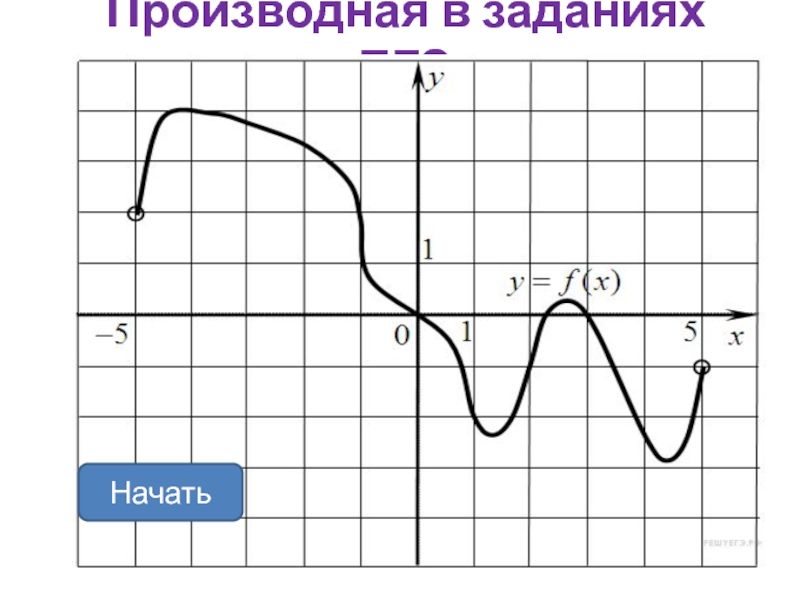
Производная в заданиях ЕГЭ
Содержание
- 1. Производная в заданиях ЕГЭ
- 2. ОглавлениеФизический смысл производнойГеометрический смысл производнойПрименение производной к исследованию функции
- 3. Пример 1:Физический смысл производнойЕсли точка движется вдоль
- 4. Пример 1. Физический смысл производнойМатериальная точка движется
- 5. Пример 2: Физический смысл производнойМатериальная точка движется
- 6. Пример 3: Физический смысл производнойМатериальная точка M начинает движение
- 7. Геометрический смысл производнойПроизводная в точке x0 равна угловому
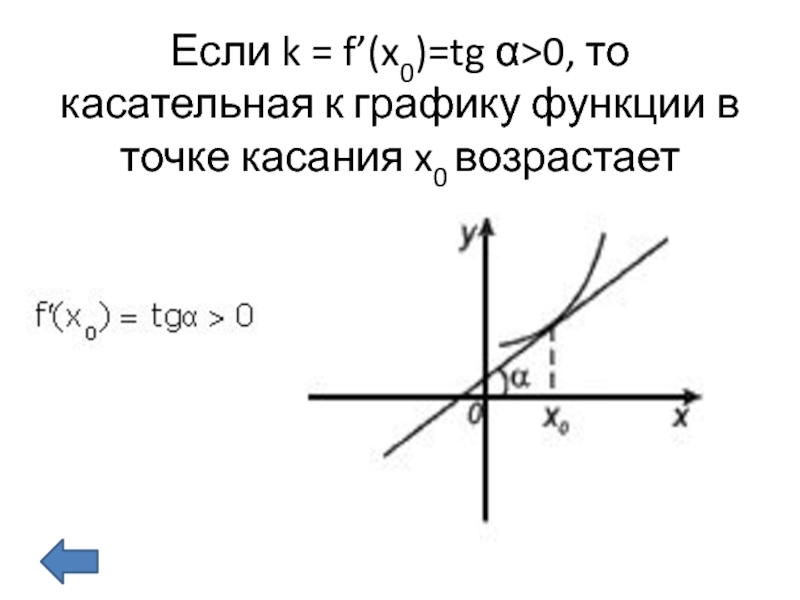
- 8. Если k = f’(x0)=tg α>0, то касательная к графику функции в точке касания x0 возрастает
- 9. Если k = f’(x0)=tg α
- 10. Если k = f’(x0)=tg α=0, то касательная
- 11. В точке Е касательная к графику горизонтальна, и производная равна
- 12. В точке F максимума или минимума производная не существует.
- 13. Пример 1На рисунке изображен график функции y = f(x), определенной
- 14. Пример 2Ответ: 5На рисунке изображен график производной
- 15. Пример 3Ответ: 2На рисунке изображён график функции y=f(x) и
- 16. Пример 4Ответ: 1,25Решение: Поскольку касательная проходит через
- 17. Применение производной к исследованию функцииЭкстремумы функции Монотонность
- 18. Экстремумы функции Определение 1: Точки x0 называются
- 19. Монотонность функции Определение 1: Функция y=f(x), определенная
- 20. Наибольшее и наименьшее значение функцииОпределение 1: Функция
- 21. Пример 1На рисунке изображен график производной функции
- 22. Пример 2 2. На рисунке изображен график функции y=f(x),
- 23. Пример 3 На рисунке изображен график функции y = f(x),
- 24. Пример 4 На рисунке изображён график y
- 25. Пример 5 НазадДалееНа рисунке изображен график производной
- 26. Пример 6 НазадНа рисунке изображен график производной
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Оглавление
Физический смысл производной
Геометрический смысл производной
Применение производной к исследованию функции
Слайд 3Пример 1:
Физический смысл производной
Если точка движется вдоль оси и ее координаты
изменяются по закону x(t), то мгновенная скорость точки:
оглавлениюСлайд 4Пример 1. Физический смысл производной
Материальная точка движется прямолинейно по закону
, где x(t) — расстояние от точки
отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9.Решение:
Скорость движения материальной точки есть производная расстояния в момент времени.
Ответ: 60.
Назад
К следующему примеру
Слайд 5Пример 2: Физический смысл производной
Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Решение.
Найдем закон изменения скорости:
Чтобы найти, в какой момент времени скорость была равна 3 м/с, решим уравнение:
Ответ: 8.
Назад
К следующему примеру
Слайд 6Пример 3: Физический смысл производной
Материальная точка M начинает движение из точки A и движется
по прямой на протяжении 12 секунд. График показывает, как менялось
расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
Решение.Мгновенная скорость равна производной перемещения по времени. Значение производной равно нулю в точках экстремума функции s(t). Точек экстремума на графике 6.
Ответ: 6
Назад
Проверь себя!
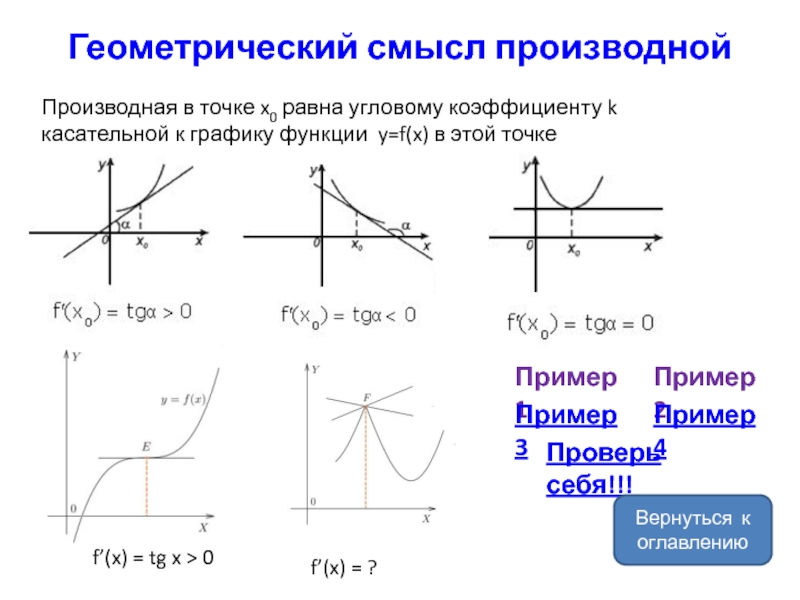
Слайд 7Геометрический смысл производной
Производная в точке x0 равна угловому коэффициенту k касательной
к графику функции y=f(x) в этой точке
f’(x) = ?
Пример 1
Пример 2
Пример 3
Пример 4
Проверь себя!!!
Вернуться к оглавлению
f’(x) = tg x > 0
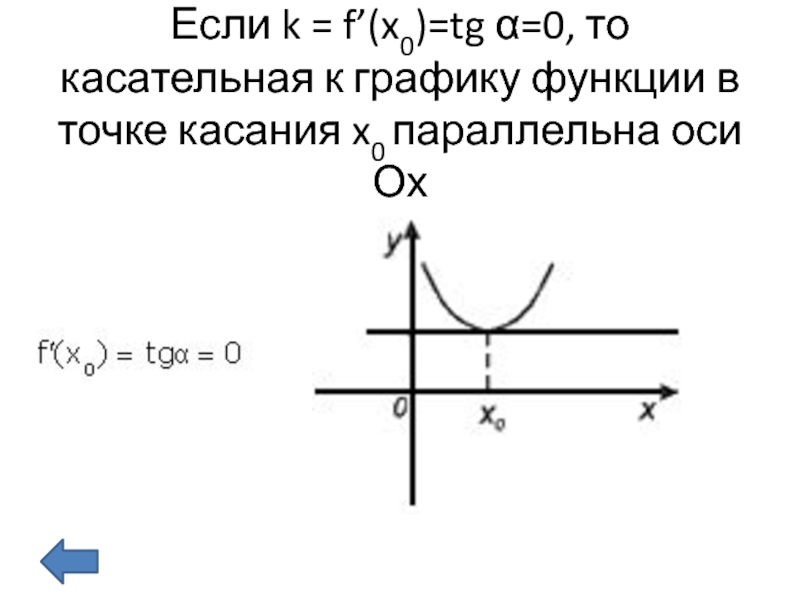
Слайд 10Если k = f’(x0)=tg α=0, то касательная к графику функции
в точке касания x0 параллельна оси Ох
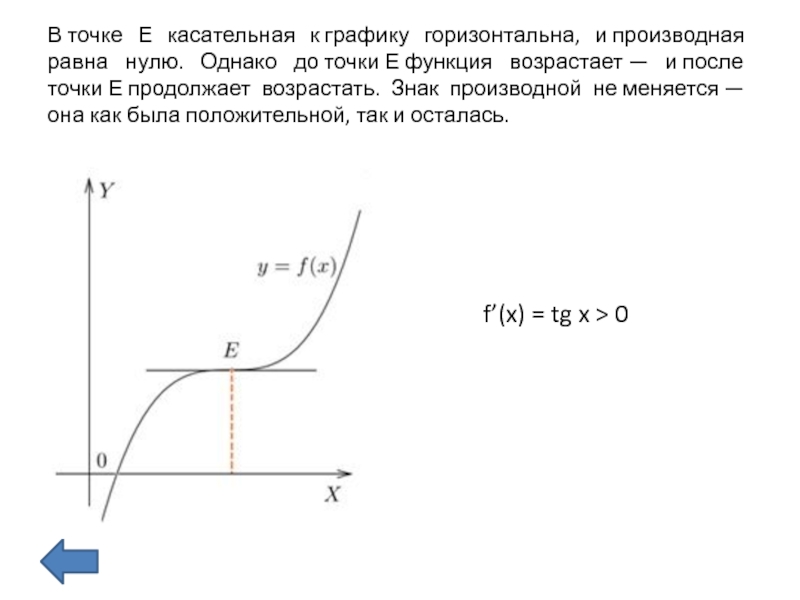
Слайд 11В точке Е касательная к графику горизонтальна, и производная равна нулю. Однако до точки Е функция
возрастает — и после точки Е продолжает возрастать. Знак производной не меняется — она как была
положительной, так и осталась.f’(x) = tg x > 0
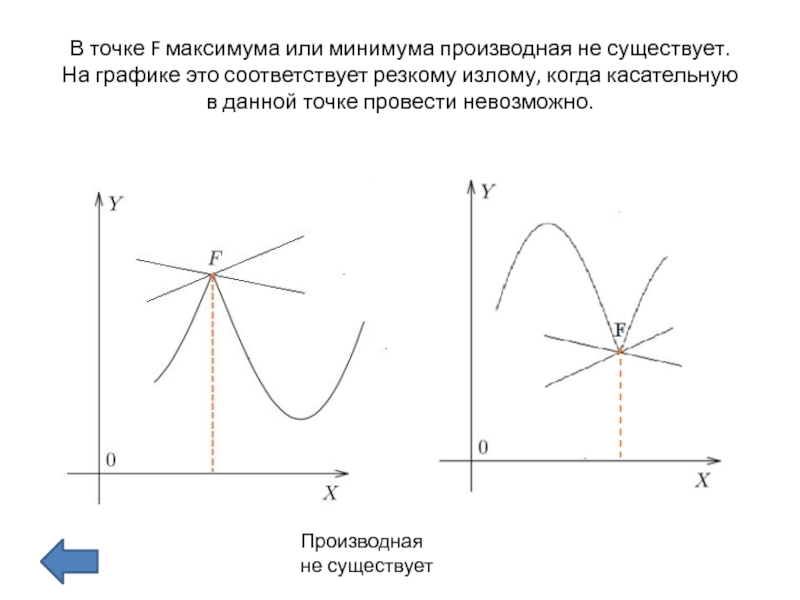
Слайд 12В точке F максимума или минимума производная не существует. На графике это соответствует
резкому излому, когда касательную в данной точке провести невозможно.
Производная не существует
Слайд 13Пример 1
На рисунке изображен график функции y = f(x), определенной на интервале (−5;
5). Найдите количество точек, в которых касательная к графику функции
параллельна прямой y = 6 или совпадает с ней.y = 6
Х 1
Х 2
Х 3
Х 4
Ответ: 4
6
Назад
К следующему примеру
Слайд 14Пример 2
Ответ: 5
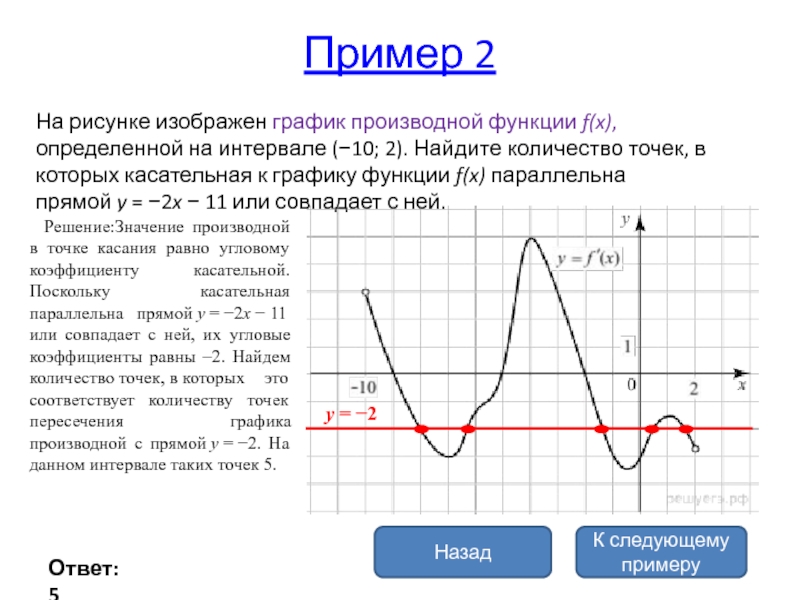
На рисунке изображен график производной функции f(x), определенной на
интервале (−10; 2). Найдите количество точек, в которых касательная к графику
функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.Решение:Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = −2x − 11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой y = −2. На данном интервале таких точек 5.
y = −2
Назад
К следующему примеру
Слайд 15Пример 3
Ответ: 2
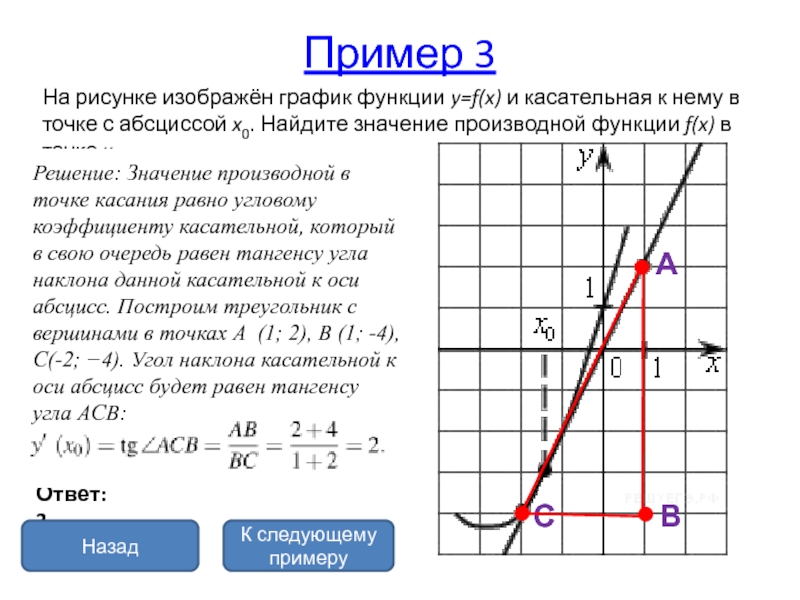
На рисунке изображён график функции y=f(x) и касательная к нему
в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
С
А
Решение: Значение
производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; -4), C(-2; −4). Угол наклона касательной к оси абсцисс будет равен тангенсу угла ACB:В
Назад
К следующему примеру
Слайд 16Пример 4
Ответ: 1,25
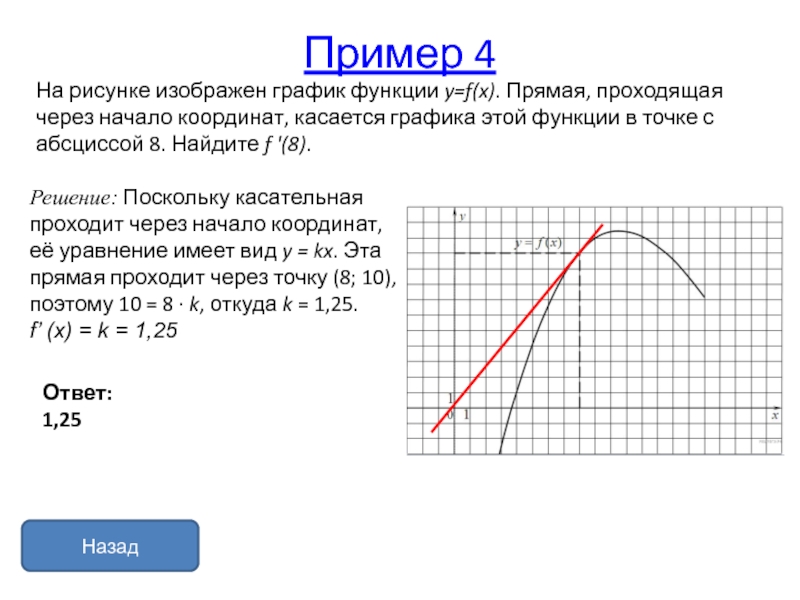
Решение: Поскольку касательная проходит через начало координат, её
уравнение имеет вид y = kx. Эта прямая проходит через точку (8; 10),
поэтому 10 = 8 · k, откуда k = 1,25.f’ (x) = k = 1,25
На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f '(8).
Назад
Слайд 17Применение производной к исследованию функции
Экстремумы функции
Монотонность функции
Наибольшее и
наименьшее значение функции
Вернуться к оглавлению
Пример 1
Пример 2
Пример 3
Пример 6
Пример
5Пример 4
Проверь себя!!!
Слайд 18Экстремумы функции
Определение 1: Точки x0 называются точками экстремума функции,
если они являются точками максимума и минимума для функции f(x).
Определение
2: Точка x0 называется критической точкой функции f(x), если: x0 - внутренняя точка области определения;
2) f′(x0)=0 или не существует.
Достаточное условие экстремума
Пусть точка x0 является критической для функции y=f(x) и лежит в интервале (a,b). На каждом интервале (a,x0) и (x0,b) производная f′(x) существует и сохраняет постоянный знак.
Если на интервале (a,x0) f′(x)>0, а на интервале (x0,b) f’(x)<0, то точка х0 – точка максимума
Если на интервале (a,x0) f′(x)<0, а на интервале (x0,b) f’(x)>0, то точка x0 - точка минимума.
Если и на интервале (a,x0), и на интервале (x0,b) f′(x)>0 или f’(x)<0, то точка х0 – точка перегиба
Назад
Далее
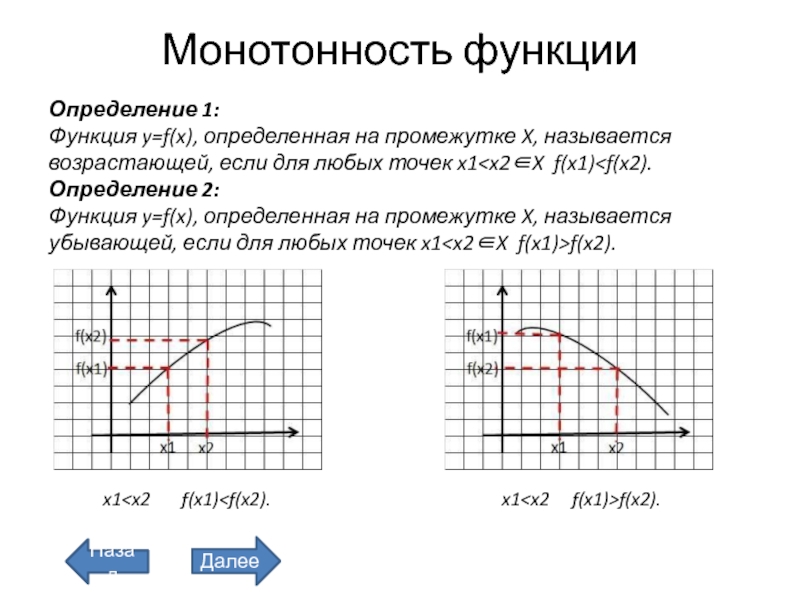
Слайд 19Монотонность функции
Определение 1:
Функция y=f(x), определенная на промежутке X,
называется возрастающей, если для любых точек x1
y=f(x), определенная на промежутке X, называется убывающей, если для любых точек x1x1 x1 Назад Далее
Слайд 20Наибольшее и наименьшее значение функции
Определение 1:
Функция y=f(x), определенная на
промежутке X, достигает своего наибольшего значения, если существует точка x0∈X,
такая, что для всех x∈X выполняется неравенство f(x)≤f(x0)Определение 2:
Функция y=f(x), определенная на промежутке X, достигает своего наименьшего значения, если существует точка x0∈X, такая, что для всех x∈X выполняется неравенство f(x)≥f(x0)
Назад
Далее
Слайд 21Пример 1
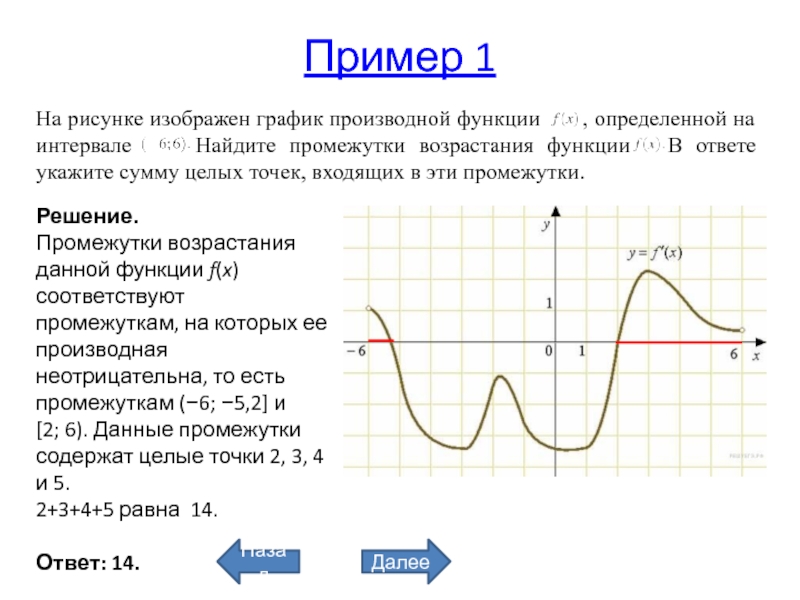
На рисунке изображен график производной функции , определенной
на интервале Найдите промежутки возрастания функции В ответе укажите
сумму целых точек, входящих в эти промежутки.Решение.
Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых ее производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6). Данные промежутки содержат целые точки 2, 3, 4 и 5.
2+3+4+5 равна 14.
Ответ: 14.
Назад
Далее
Слайд 22Пример 2
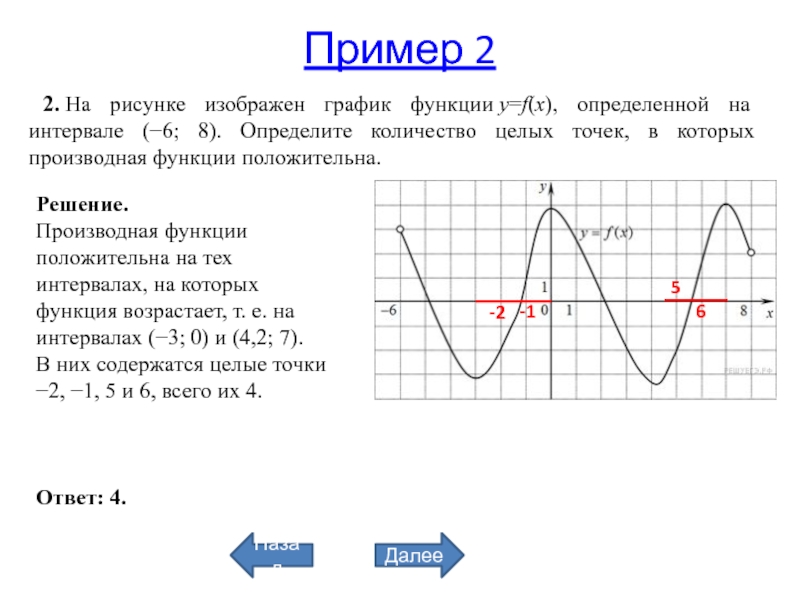
2. На рисунке изображен график функции y=f(x), определенной на интервале
(−6; 8). Определите количество целых точек, в которых производная функции
положительна.Решение.
Производная функции положительна на тех интервалах, на которых функция возрастает, т. е. на интервалах (−3; 0) и (4,2; 7).
В них содержатся целые точки −2, −1, 5 и 6, всего их 4.
Ответ: 4.
Назад
Далее
-2
-1
5
6
Слайд 23Пример 3
На рисунке изображен график функции y = f(x), определенной на интервале
(−2; 12). Найдите сумму точек экстремума функции f(x).
Ответ: 44.
Решение.
Заданная функция имеет максимумы
в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
4
9
11
2
7
10
Назад
Далее
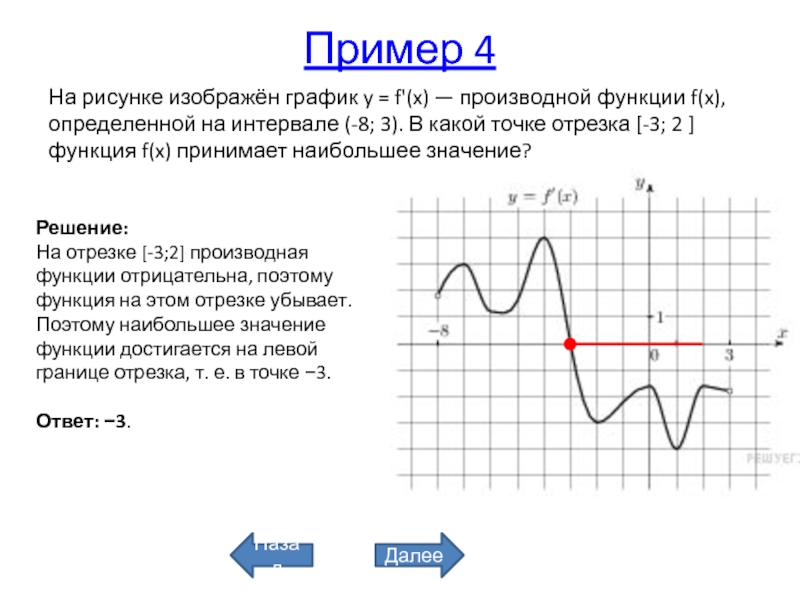
Слайд 24Пример 4
На рисунке изображён график y = f'(x) —
производной функции f(x), определенной на интервале (-8; 3). В какой
точке отрезка [-3; 2 ] функция f(x) принимает наибольшее значение?Решение:
На отрезке [-3;2] производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе отрезка, т. е. в точке −3.
Ответ: −3.
Назад
Далее
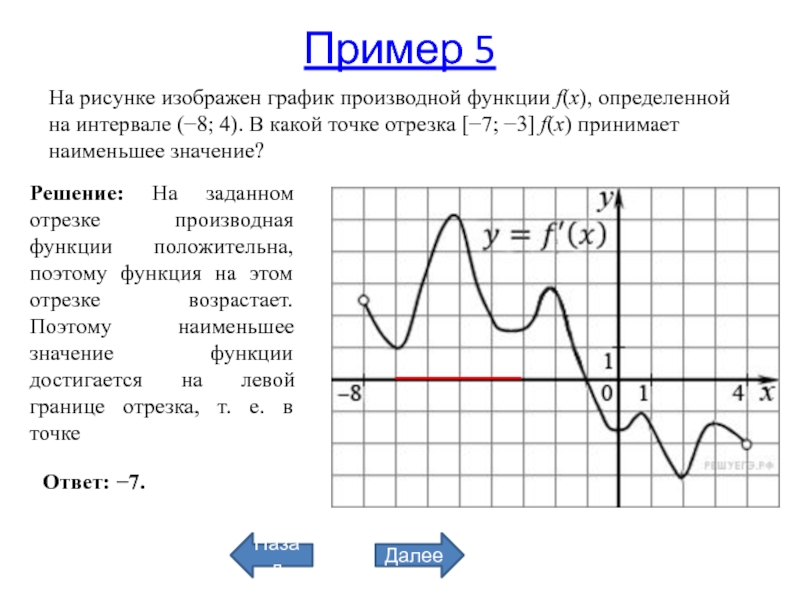
Слайд 25Пример 5
Назад
Далее
На рисунке изображен график производной функции f(x), определенной на
интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает
наименьшее значение?Решение: На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Поэтому наименьшее значение функции достигается на левой границе отрезка, т. е. в точке
Ответ: −7.
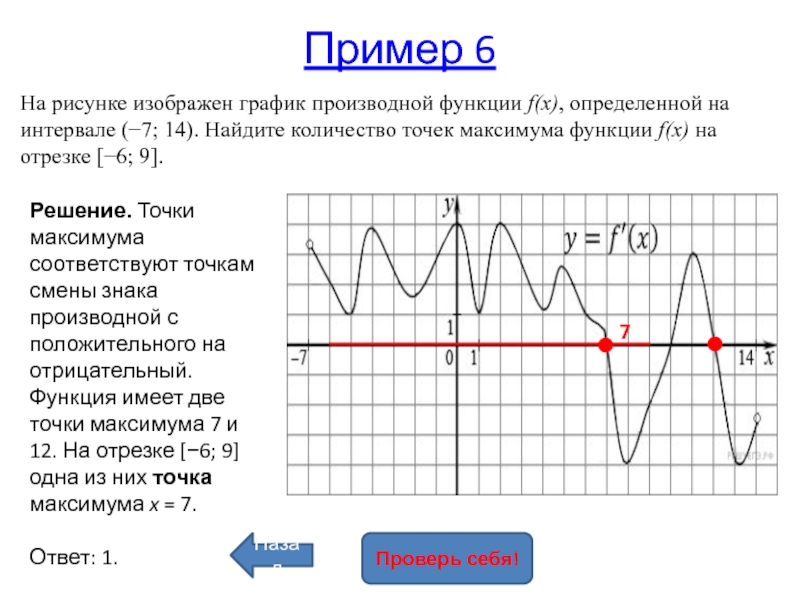
Слайд 26Пример 6
Назад
На рисунке изображен график производной функции f(x), определенной на
интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].
Решение. Точки
максимума соответствуют точкам смены знака производной с положительного на отрицательный. Функция имеет две точки максимума 7 и 12. На отрезке [−6; 9] одна из них точка максимума x = 7.Ответ: 1.
7
Проверь себя!