Устойчивость дискретных систем

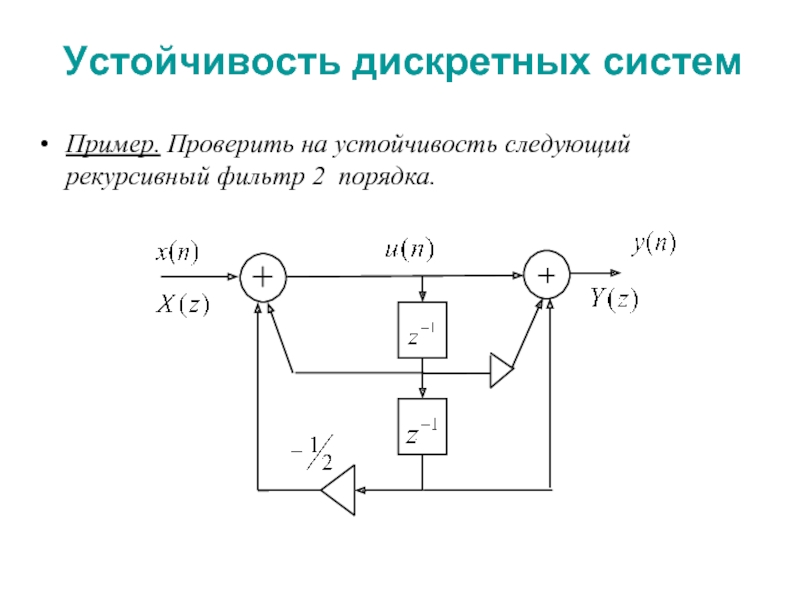
постоянными параметрами (стационарный фильтр) называется устойчивой, если при любых начальных

условиях и любом ограниченном входном сигнале выходной сигнал также остается ограниченным, то есть из условия для всех следует

Необходимым и достаточным условием устойчивости одномерного стационарного линейного фильтра является следующее требование к его импульсной характеристике:

(13.1)

не выполняется, то есть

.
Рассмотрим ограниченную последовательность, заданную значениями:

Так как выходные отсчеты сигнала равны свертке входных отсчетов и значений импульсной характеристики дискретной системы, то есть

то при отклик системы равен:

вход поступает ограниченная последовательность отсчетов сигнала

. Из формулы свертки входного сигнала и импульсной характеристики получаем:



Если , то

и система – устойчива.

нерекурсивных дискретных системах для вычисления очередного отсчета выходного сигнала

используются только отсчеты входного сигнала
. Поэтому алгоритм работы такой системы имеет вид:


Системная (передаточная) функция такой системы является рациональной функцией, то есть полиномом степени комплексного аргумента :

импульсные характеристики имеют конечное число

ненулевых отсчетов, причем эти отсчеты равны коэффициентам алгоритма фильтрации.
Действительно

Отсюда следует, что

Таким образом, импульсная характеристика нерекурсивного стационарного линейного фильтра имеет конечное число отличных от нуля отсчетов, и в соответствии с (13.1) такой фильтр всегда устойчив.

использовать критерий устойчивости в форме (13.1) затруднительно, поскольку необходимо суммировать

бесконечный ряд модулей отсчетов импульсной характеристики. Выразим критерий (13.1) в другой форме, удобной для исследования рекурсивных фильтров.
Рассмотрим физически реализуемый фильтр порядка с системной функцией и для простоты предположим, что все полюсы простые. Отметим, что для физически реализуемых фильтров степень полинома в числителе не превышает степень полинома в знаменателе.

имеем:



а при

имеем следующее выражение:

, полагая при

этом что , можно записать следующее соотношение:




Из анализа этого соотношения следует:


Так как по условию , то ряд в правой части соотношения сходится и

лежат внутри круга единичного радиуса Z-плоскости, то такой

фильтр устойчив. Если хотя бы один полюс расположен на единичной окружности или во внешней части круга единичного радиуса, то такая представляет неустойчивый фильтр. Заметим, что положение нулей системной функции не влияет на устойчивость фильтра.
Недостатки полюсного критерия устойчивости обусловлены необходимостью определения корней характеристического уравнения, являющихся полюсами системной функции. Аналитических методов решения алгебраических уравнений, порядок которых выше четвертого, не существует. Поэтому нахождение полюсов высокого порядка возможно лишь численными методами.

порядка.

Z-преобразованной форме:



Из них определяем системную функцию такого фильтра:


где

корни характеристического уравнения, являющиеся
полюсами системной функции. Так как и
, следовательно, полюса системной функции лежат внутри круга единичного радиуса, и фильтр является устойчивым.